Giáo án Hình học Lớp 8 - Tiết 23 đến 24 - Phạm Nguyễn Sĩ Thắng
I. MỤC TIÊU:
Qua tiết này HS cần:
- Hệ thống hoá kiến thức ở chương I về tứ giác. Định nghĩa , tính chất, dấu hiệu nhận biết các tứ giác đặc biệt đã học. Thấy được mối liên hệ giữa các hình đó.
- Vận dụng được những kiến thức trên để rèn luyện kỹ năng nhận biết hình, chứng minh, tính toán, tìm điều kiện của một hình để thoả mãn một tính chất nào đó.
- Rèn luyện tư duy lôgic, thao tác phân tích và tổng hợp.
II. CHUẨN BỊ:
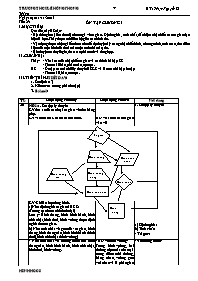
Thầy: - Vẽ sẵn sơ đồ nhận biết tứ giác và các hình bài tập 88
- Thước kẻ êke, phấn màu, compa.
HS - Ôn tập các câu hỏi lý thuyết ở SGK và làm các bài tập ôn tập
- Thước kẻ, êke, compa.
III. TIẾN TRÌNH TIEÁT DAÏY:
1. Ổn định (1’)
2. Kiểm tra: (trong phần ôn tập)
3. Bài mới:
Bạn đang xem tài liệu "Giáo án Hình học Lớp 8 - Tiết 23 đến 24 - Phạm Nguyễn Sĩ Thắng", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày soạn: 11/11/2005 Tiết 23: ÔN TẬP CHƯƠNG I I. MỤC TIÊU: Qua tiết này HS cần: - Hệ thống hoá kiến thức ở chương I về tứ giác. Định nghĩa , tính chất, dấu hiệu nhận biết các tứ giác đặc biệt đã học. Thấy được mối liên hệ giữa các hình đó. - Vận dụng được những kiến thức trên để rèn luyện kỹ năng nhận biết hình, chứng minh, tính toán, tìm điều kiện của một hình để thoả mãn một tính chất nào đó. - Rèn luyện tư duy lôgic, thao tác phân tích và tổng hợp. II. CHUẨN BỊ: Thầy: - Vẽ sẵn sơ đồ nhận biết tứ giác và các hình bài tập 88 - Thước kẻ êke, phấn màu, compa. HS - Ôn tập các câu hỏi lý thuyết ở SGK và làm các bài tập ôn tập - Thước kẻ, êke, compa. III. TIẾN TRÌNH TIEÁT DAÏY: 1. Ổn định (1’) 2. Kiểm tra: (trong phần ôn tập) 3. Baøi môùi: TL Hoạt động của thầy Hoạt động của trò Noäi dung 20’ HÑ1: 1. Ôn tập lý thuyết GV đưa sơ đồ các loại tứ giác vẽ trên bảng phụ. 1. Ôn tập lý thuyết GV: Yêu cầu HS trả lời các câu hỏi. HS: vẽ sơ đồ các tứ giác vào vở Tứ giác Hình bình hành Hình thoi Hình vuông Hình chữ nhật Hình thang vuông Hình thang Hình thang cân GV: Chỉ lần lượt từng hình. a) Nêu định nghĩa tứ giác ABCD. (Tương tự cho các hình còn lại) Lưu ý: Hình thang, hình bình hành, hình chữ nhật, hình thoi, hình vuông được định nghĩa theo tứ giác. a) Ñònh nghóa: b) Nêu tính chất về góc của: tứ giác, hình thang, hình thang cân, hình bình hành (hình thoi), hình chữ nhật (hình vuông) b) Tính chaát: - Veà goùc: - Nêu tính chất về đường chéo của hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuông. - HS: vẽ hình vuông: Trong hình vuông, hai đường chéo cắt nhau tại trung điểm mỗi đường, bằng nhau, vuông góc với nhau và là phân giác của các góc hình vuông. - Về đường chéo: - Về tính đối xứng - Trong các tứ giác đã học hình nào có trục đối xứng có tâm đối xứng? - HS: Hình vuông có 4 trục đối xứng (hai trục của hình chữ nhật, hai trục của hình thoi) và một tam đối xứng là giao điểm 2 đường chéo. s Trong khi trả lời về tính chất các hình GV vẽ thêm vào hình đường chéo, trục đối xứng, kí hiệu bằng nhau, vuông góc để minh hoạ. c) Nêu dấu hiệu nhận biết các hình? Hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuông. - HS: trả lời miệng các dấu hiệu nhận biết. c) Về dấu hiệu nhận biết 18’ HÑ2: Luyện tập: 2. Luyeän taäp: 1. Bài tập 88/111 SGK - GV cho HS làm bài tập 88 SGK/111 a) Tứ giác EFGH là hình bình hành. chứng minh H D G C F B E A s Gọi 1 HS đọc đề bài và vẽ hình vào vở. - 1 HS đọc đề bài DABC có: AE = EB (gt) FB = FC (gt) => EF là đường trung bình của DABC. => EF//AC và EF=. Ch/ minh tương tự HG//AC; HG =,và EH//BD; EH s Tứ giác EFGH là hình gì? chứng minh? Vậy EFGH là hình chữ nhật => - Các đường chéo AC, BD của tứ giác ABCD cần có điều kiện gì thì hình bình hành EFGH là hình chữ nhật? GV đưa hình vẽ minh hoạ A B E F C G D H - HS: Trả lời. = EH ^ EF => AC ^ BD A B E F G D H - Các đường chéo AC và BD cần điều kiện gì thì hình bình hành EFGH là hình thoi? GV đưa hình vẽ minh hoạ. - HS trả lời.. b) Hình bình hành EFGH là hình thoi => EH = EF => BD = AC (Vì EH = ) - Các đường chéo AC và BD cần điều kiện gì thì hình bình hành EFGH là hình vuông? GV đưa hình vẽ minh hoạ. A B E F C G D H - HS: Trả lời c) Hình bình hành EFGH là hình vuông. => EFGH vừa là hình chữ nhật vừa là hình thoi. => AC ^ BD => AC = BD 4’ HÑ3:Củng cố: GV đưa hình vẽ 109 SGK/111 (SBT 87) - HS: trả lời: Hình chữ nhật Hình thoi Hình bình hành Hình thang H.vuông Yêu cầu HS điền vào dấu trong các câu hỏi a); b); c). a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang. a) Tập hợp các hình thoi tập hợp con của tập hợp các hình bình hành, hình thang. c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông. 4. Höôùng daãn veà nhaø: (2’) Ôn tập định nghĩa, tính chất, dấu hiệu nhận biết các hình tứ giác, phép đối xứng qua trục, qua tâm. - Bài tập về nhà: 89 SGK/111, 159, 161, 162 SBT/76 – 77. IV. RUÙT KINH NGHIEÄM, BOÅ SUNG: Lớp : 8A KIỂM TRA:15 ph Họ và tên:........................................... HÌNH HỌC 8 Điểm: Lời phê: Đề: Cho tam giác ABC. Từ một điểm M trên BC vẽ các đường thẳng vẽ các đường thẳng song song với AB và AC, chúng lần lượt cắt AB tại I và AC tại K. Gọi O là trung điểm của AM . Chứng minh O là trung điểm của IK. Bài làm: Lớp : 8A/... KIỂM TRA: 1TIẾT Họ và tên:........................................... HÌNH HỌC 8 Điểm: Lời phê: Đề: Câu 1: (2đ) Điền đấu “X” vào ô trống thích hợp: TT Câu Đúng Sai 1 Tổng số đo bốn góc của một tứ giác bằng 3600 2 Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi. 3 Tứ giác có bốn cạnh bằng nhau và có một góc vuông là hình vuông. 4 Hình thang có một góc vuông là hình chữ nhật. Câu 2:(2đ) Cho tam giác ABC, BC = 16 cm, AB = AC = 10cm. Lấy D đối xứng với C qua A.(Đánh “X” vào kết quả đúng) a) ; b) c) BD = cm ; d) BD = 12 cm Câu 3:(6đ) Cho tam giác ABC. Đường trung tuyến AM.Gọi I là trung điểm của AC, D là điểm đối xứng với M qua I. Tứ giác AMCD là hình gì? vì sao? Nếu tam giác ABC có thì tứ giác AMCD là hình gì? vì sao? Tìm điều kiện của tam giác ABC để tứ giác AMCD là hình vuông. BÀI LÀM: Ngày soạn: 12 / 11 / 2005 Tiết 24 KIỂM TRA 1 TIẾT I. MỤC TIÊU : - Kiểm tra kiến thức ở chương I về tứ giác. Định nghĩa , tính chất, dấu hiệu nhận biết các tứ giác đặc biệt đã học và mối liên hệ giữa các hình đó. - Kiểm tra việc vận dụng những kiến thức trên để nhận biết hình, chứng minh, tính toán, tìm điều kiện của một hình để thoả mãn một tính chất nào đó. II ĐỀ BÀI : Câu 1: (1,5 đ) Điền đấu “X” vào ô trống thích hợp: Caâu Noäi dung Đúng Sai 1 Hình thang có một góc vuông là hình chữ nhật. 2 Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường là hình thoi. 3 Tứ giác có bốn cạnh bằng nhau và có một góc vuông là hình vuông. 4 Tổng số đo bốn góc của một tứ giác bằng 3600 5 Hình thang coù hai caïnh beân baèng nhau laø hình thang caân. 6 Hình thoi laø moät hình thang caân. Câu 2:(1 đ) Cho tam giác ABC, BC = 16 cm, AB = AC = 10cm. Lấy D đối xứng với C qua A.(Đánh “X” vào kết quả đúng) a) ; b) c) BD = 12 cm ; d) BD = cm Caâu 3: (1 ñ) Choïn caâu traû lôøi ñuùng Moät hình vuoâng coù caïnh baèng 4 cm, ñöôøng cheùo cuûa hình vuoâng ñoù baèng: A. 8 cm B. C. 6 cm D. 16 cm Câu 3:(5 đ) Cho tam giác ABC. Đường trung tuyến AM.Gọi I là trung điểm của AC, D là điểm đối xứng với M qua I. Tứ giác AMCD là hình gì? vì sao? Nếu tam giác ABC có thì tứ giác AMCD là hình gì? vì sao? Tìm điều kiện của tam giác ABC để tứ giác AMCD là hình vuông. Caâu 4: (1,5 ñ) Cho töù giaùc ABCD (AB khoâng song song vôùi CD). Goïi M, N laàn löôït laø trung ñieåm cuûa caùc caïnh AB vaø CD thoaû maõn . Chöùng minh raèng ABCD laø hình thang. III. ÑAÙP AÙN VAØ BIEÅU ÑIEÅM: Câu 1 : 1,5 điểm 1) S, 2) Đ, 3) Đ, 4) Đ. Câu 2 : 1điểm Chọn : b), c). Caâu 3: 1 ñieåm choïn : B Câu 3 : 5 điểm. Hình veõ ñuùng 0,5 ñ. a) AMCD là hình bình hành, vì có hai đường chéo cắt nhau tại trung điểm mỗi đường. (1,5 đ) b) AMCD là hình thoi, vì có AM = MC ( = BM = BC/2 ) (2 đ) c) Tam giác ABC vuông cân tại A thì tứ giác AMCD là hình vuông. (1đ) Caâu 4: 1,5 ñieåm. Hình veõ ñuùng 0,5 ñieåm B C M I N A D Goïi I laø trung ñieåm cuûa BD Chöùng minh IN // BC, IN = ½ BC; IM // AD, IM = ½ AD (0,5 ñieåm) Maët khaùc: Do ñoù: MM = IN + IM Þ M, I, N thaúng haøng Do ñoù: BC // AD Þ ABCD laø hình thang (0,5 ñieåm) IV. THỐNG KÊ : Lôùp Só soá 9 - 10 7 - 8 5 - 6 3 - 4 0 à 2 SL % SL % SL % SL % SL % V. RUÙT KINH NGHIEÄM, BOÅ SUNG:
Tài liệu đính kèm:
 giao_an_hinh_hoc_lop_8_tiet_23_den_24_pham_nguyen_si_thang.doc
giao_an_hinh_hoc_lop_8_tiet_23_den_24_pham_nguyen_si_thang.doc





