Giáo án Hình học Lớp 8 - Tiết 1+2 - Năm học 2009-2010 - Trần Duy Ánh
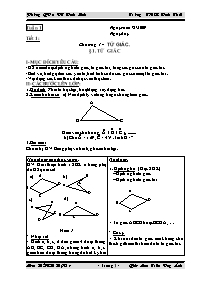
đoạn thẳng nào cũng không nằm trên một đường thẳng. Các hình a, b, c gọi là tứ giác.
- Hình d có 2 đoạn thẳng BC, CD nằm trên một đường thẳng. Hình d không là tứ giác.
HS: Phát biểu định nghĩa tứ giác.
GV: Nhấn mạnh hai ý: Tứ giác là hình:
– Gồm bốn đoạn thẳng “khép kín”.
– Bất kỳ hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
GV: H/d cách đọc tên tứ giác.
HS: Đọc tên tứ giác ABCD, BCDA, .
GV: Giới thiệu đỉnh, cạnh của tứ giác.
HS: Đọc tên đỉnh, cạnh của tứ giác ABCD
GV: Cho HS trả lời ở SGK.
- Ở hình 1 tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác?
HS: Quan sát và trả lời hình 1a SGK
GV: Hãy giải thích vì sao hình 1b, 1c không có tính chất như hình 1a?
HS: Giải thích.
GV: Giới thiệu định nghĩa tứ giác lồi.
HS: Nêu định nghĩa tứ giác lồi.
GV: – Qui ước khi nói đến tứ giác mà không chú thích gì thêm thì hiểu đó là tứ giác lồi.
– Giới thiệu các định nghĩa:
+ Hai đỉnh kề nhau, hai đỉnh đối nhau.
+ Hai cạnh kề nhau, hai cạnh đối nhau.
+ Đường chéo, góc, điểm trong, điểm ngoài của tứ giác.
Tuần 1 Ngày soạn: /8/2009 Ngày dạy: Tiết 1: Chương I - TỨ GIÁC. §1. TỨ GIÁC I- MỤC ĐÍCH YÊU CẦU: - HS nắm được định nghĩa tứ giác, tứ giác lồi, tổng các góc của tứ giác lồi. - Biết vẽ, biết gọi tên các yếu tố, biết tính số đo các góc của một tứ giác lồi . -Vận dụng các kiến thức đã học vào thực tiễn. II- CÁC BƯỚC LÊN LỚP: 1. Ổn định: Phân tổ học tập, hoạt động xây dựng bài. 2. Kiểm tra bài cũ: a) Nêu định lý về tổng ba góc trong tam giác. A B C Ù Ù Ù Ù Ù Ù Điền vào chổ trống: A + B + C = ........ b) Cho A = 1100, C = 450 .Tính B =? 3. Bài mới: Chuẩn bị: GV: Bảng phụ vẽ hình, ghi sẵn bài tập. Hoạt động của thầy và trò: GV: Giới thiệu hình 1 SGK ở bảng phụ để HS quan sát: × c) D C B C D B A D C A B C D B A A a) b) d) Hình 1 * Nhận xét: - Hình a, b, c, d đều gồm 4 đoạn thẳng AB, BC, CD, DA, nhưng hình a, b, c gồm bốn đoạn thẳng trong đó bất kỳ hai đoạn thẳng nào cũng không nằm trên một đường thẳng. Các hình a, b, c gọi là tứ giác. - Hình d có 2 đoạn thẳng BC, CD nằm trên một đường thẳng. Hình d không là tứ giác. HS: Phát biểu định nghĩa tứ giác. GV: Nhấn mạnh hai ý: Tứ giác là hình: – Gồm bốn đoạn thẳng “khép kín”. – Bất kỳ hai đoạn thẳng nào cũng không nằm trên một đường thẳng. GV: H/d cách đọc tên tứ giác. HS: Đọc tên tứ giác ABCD, BCDA, . GV: Giới thiệu đỉnh, cạnh của tứ giác. ?1 HS: Đọc tên đỉnh, cạnh của tứ giác ABCD GV: Cho HS trả lời ở SGK. - Ở hình 1 tứ giác nào luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác? HS: Quan sát và trả lời hình 1a SGK GV: Hãy giải thích vì sao hình 1b, 1c không có tính chất như hình 1a? HS: Giải thích. GV: Giới thiệu định nghĩa tứ giác lồi. HS: Nêu định nghĩa tứ giác lồi. GV: – Qui ước khi nói đến tứ giác mà không chú thích gì thêm thì hiểu đó là tứ giác lồi. – Giới thiệu các định nghĩa: + Hai đỉnh kề nhau, hai đỉnh đối nhau. + Hai cạnh kề nhau, hai cạnh đối nhau. ?2 + Đường chéo, góc, điểm trong, điểm ngoài của tứ giác. HS: Thực hiện SGK. ?3 - Quan sát tứ giác ABCD ở bảng phụ rồi điền vào chổ trống: GV: Cho HS thực hiện SGK. - Nhắc lại định lý tổng ba góc trong tam giác. Ù Ù Ù Ù – Vẽ tứ giác ABCD. Tính tổng: A + B + C + D = ? A B C D GV: Cho một hs lên cắt một tứ giác bằng bìa cứng theo một đường chéoAC thành hai tam giác: ∆ BAC và : ∆ DAC Ù Ù Ù Ù Ù Ù HS: Nhận xét A = BAC + DAC C = BCA + DCA GV: Từ đó muốn tính tổng các góc của một tứ giác ta kẻ thêm đường nào? Ù Ù Ù Ù HS: Kẻ thêm đường chéo AC hay BD để có hai tam giác. GV: A/d định lý nào tính A + B + C + D HS: Định lý tổng ba góc trong tam giác. Ù Ù Ù Ta có BAC + B + BCA = 1800 Ù Ù Ù DAC + D + DCA = 1800 Ù Ù Ù Ù Ù Ù BAC + B + BCA + DAC + D + DCA Ù Ù Ù Ù Ù Ù = 3600 Ù Ù Ù Ù (BAC+ BCA) + B + (DAC+ DCA) + D = 3600 A + B + C + D = 3600 GV: Cho hs phát biểu định lý tổng các góc của một tứ giác. HS: Vẽ hình, viết GT, KL. Nội dung: 1. Định nghĩa: (Học SGK) – Định nghĩa tứ giác – Định nghĩa tứ giác lồi C D B A - Tứ giác ABCD hoặc BCDA, . * Chú ý: - Khi nói đến tứ giác mà không chú thích gì thêm thì hiểu đó là tứ giác lồi. ?2 Điền vào chổ trống: ( Xem SGK) 2. Tổng các góc của một tứ giác: Định lý: (Học SGK) B D C A GT ABCD: tứ giác. Ù Ù Ù Ù KL A + B + C + D = 3600 Chứng minh: Ù Ù Ù Ta có BAC + B + BCA = 1800 Ù Ù Ù DAC + D + DCA = 1800 Ù Ù Ù Ù Ù Ù BAC + B + BCA + DAC + D + DCA Ù Ù Ù Ù Ù Ù = 3600 Ù (BAC+ BCA) + B +(DAC+ DCA)+D = 3600Ù Ù Ù A + B + C + D = 3600 4. Cũng cố: – HS nhắc lại định nghĩa tứ giác, định nghĩa tứ giác lồi, định lý tổng các góc của một tứ giác. – GV cho HS thực hiện bài tập 1, 2, ở SGK trên bảng phụ, hướng dẫn, gợi ý hs bài tập về nhà 3, 4, 5 ở SGK. 5. Dặn dò: – Học thuộc định nghĩa tứ giác, định nghĩa tứ giác lồi, định lý tổng các góc của một tứ giác và c/m định lý đó. – Làm bt về nhà: 3, 4, 5 SGK. III- BỔ SUNG - RÚT KINH NGHIỆM: chị nhân SDT 0915011039 Tiết 2 Ngày soạn: Ngày dạy: §2. HÌNH THANG I - MỤC ĐÍCH YÊU CẦU: - HS nắm được định nghĩa hình thang, hình thang vuông, các yếu tố của hình thang. Chứng minh được một tứ giác là hình thang, hình thang vuông. - HS vẽ được hình thang, hình thang vuông.Biết tính số đo các góc của hình thang, hình thang vuông. - Sử dụng được dụng cụ êke để kiểm tra một tứ giác là hình thang. II - LÊN LỚP: 1. Ổn định: Kiểm tra sỉ số, tổ trưởng nhận xét việc soạn bài về nhà của các bạn 2. Kiểm tra bài cũ: HS1: Định nghĩa tứ giác, tứ giác lồi? Vẽ một tứ giác lồi, đọc tên tứ giác và nêu các yếu tố: đỉnh, cạnh, góc, đường chéo, đỉnh kề đỉnh đối, cạnh kề cạnh đối. B HS2: Nêu định lí tổng các góc của một tứ giác? x 450 1100 C A T×m x ë h×nh sau ®©y: 700 D 3. Bµi míi: ChuÈn bÞ: GV: B¶ng phô cã h×nh vÏ, bµi tËp,thíc ªke - HS: Bµi tËp vÒ nhµ. Ho¹t ®éng cña thÇy vµ trß: B GV: Cho hs quan s¸t h×nh 13 ë SGK, nhËn xÐt vÞ trÝ hai c¹nh ®èi AB vµ CD cña tø gi¸c ABCD? Gi¶i thÝch? D C A 1100 700 ^ ^ HS: AB//CD. V× tæng hai gãc trong cïng phÝa bï nhau.( A + D = 1800). GV: Giíi thiÖu ®Þnh nghÜa h×nh thang.C¹nh ®¸y, c¹nh bªn, ®¸y lín, ®¸y nhá, ®êng cao. HS: Nªu ®Þnh nghÜa h×nh thang. Nªu tªn c¹nh ®¸y, c¹nh bªn, ®¸y lín, ®¸y nhá, ®êng cao h×nh thang ABCD ë h×nh vÏ. GV: Cho hs lµm bµi tËp ?1 ë SGK cã h×nh vÏ trªn b¶ng phô. a) T×m c¸c tø gi¸c lµ h×nh thang? HS: Tr¶ lêi vµ giải thÝch tø gi¸c BCD, EFGH lµ h×nh thang, IMKN kh«ng lµ h×nh thang. GV: b) Cã nhËn xÐt g× vÒ hai gãc kÒ mét c¹nh bªn cña h×nh thang? HS: Tr¶ lêi vµ g/ thÝch hai gãc kÒ mét c¹nh bªn cña h×nh thang th× bï nhau. GV: Cho hs lµm bµi tËp ?2 ë SGK cã h×nh vÏ trªn b¶ng phô. H×nh thang ABCD cã ®¸y AB,CD. a) Cho AD//BC. C/m AD = BC, AB = CD. Ta cã thÓ xÐt hai tam gi¸c nµo? HS: C/m rABC = rCDA (g.c.g) Þ AD = BC, AB = CD. GV: Cã nhËn xÐt g× vÒ h×nh thang cã hai c¹nh bªn song song? HS: H×nh thang cã hai c¹nh bªn song song th× hai c¹nh bªn b»ng nhau, hai c¹nh ®¸y b»ng nhau. GV: b) Cho AB = CD. C/m AD//BC, AD = BC. (Ta cã thÓ xÐt hai tam gi¸c nµo?) HS: C/m rABC = rCDA (c.g.c) Þ AD = BC, AD//BC. GV: Cã nhËn xÐt g× vÒ h×nh thang cã hai c¹nh ®¸y b»ng nhau? HS: H×nh thang cã hai c¹nh ®¸y b»ng nhau th× hai c¹nh bªn song song vµ b»ng nhau GV: Cho hs nªu l¹i hai nhËn xÐt ë c©u a,b ^ ^ GV: Cho hs quan s¸t h×nh 18 ë SGK (h×nh vÏ trªn b¶ng phô). Víi AB//CD, A = 900. ^ TÝnh D HS: TÝnh D = 900 GV: Giíi thiÖu ®/ nghÜa h×nh thang vu«ng. HS: Nªu l¹i ®Þnh nghÜa h×nh thang vu«ng. Néi dung: 1. §Þnh nghÜa: (Häc SGK) c¹nh bªn D C □ H c¹nh ®¸y A B c¹nh ®¸y c¹nh bªn Tø gi¸c ABCD cã AB // CD lµ mét h×nh thang. - AB vµ CD lµ c¹nh ®¸y. - AD vµ BC lµ c¹nh bªn. - AH lµ ®êng cao. ?1 (H×nh 15 SGK) B A N 600 F 1200 C D G H E I K M 600 1050 750 750 1150 a) Tø gi¸c ABCD,EFGH lµ h×nh thang, IMKN kh«ng lµ h×nh thang. b) Hai gãc kÒ mét c¹nh bªn cña h×nh thang th× bï nhau. ?2 (SGK) ABCD lµ h×nh thang cã ®¸y AB,CD. A a) Cho AD//BC. C/m AD = BC, AB =CD. 1 B ^ ^ C D 2 2 ^ ^ C/m: AD//BC Þ A 2 = C2 AB//CD Þ A1 = C1 AC: c¹nh chung Þ rABC = rCDA (g.c.g) Þ AD = BC, AB = CD. b)Cho AB =CD. C/m AD//BC, AD = BC. / A B 1 / D C 2 2 1 ^ ^ AB//CD Þ A1 = C1 AB = CD (gt) AC: c¹nh chung ^ ^ Þ rABC = rCDA (c.g.c) Þ AD = BC, A 2 = C2 B A Do ®ã AD//BC. * NhËn xÐt: Häc SGK □ 2. H×nh thang vu«ng: C D * §Þnh nghÜa: Häc SGK ^ H×nh thang ABCD cã AB//CD,A = 900, ABCD lµ h×nh thang vu«ng. 4.Cñng cè: - Cho hs nªu l¹i ®Þnh nghÜa h×nh thang, h×nh thang vu«ng, nhËn xÐt. - HS: Lµm bµi tËp 7, 8 SGK theo tæ vµ tr×nh bµy kÕt qu¶. - GV: Híng dÉn bµi tËp 6, 9, 10 SGK 5. DÆn dß: - Häc thuéc ®Þnh nghÜa h×nh thang, h×nh thang vu«ng vµ hai nhËn xÐt. - Lµm bµi tËp 6, 9, 10 SGK, 16, 17, 19, 20 SBT (hs kh¸).
Tài liệu đính kèm:
 Hinh hoc 8 Tiet 1.doc
Hinh hoc 8 Tiet 1.doc





