Bồi dưỡng học sinh giỏi môn Toán Lớp 8 - Chuyên đề: Giá trị biểu thức - Nguyễn Hữu Hạnh
I. Một số dạng tính GTBT chung:
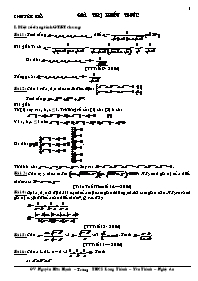
Bài 1: Tính tổng , biết
Bài giải: Ta có
Do đó:
(TTT số 9 - 2004)
Tổng quát: .
Bài 2: Cho 3 số a, b, c thoả mãn điều kiện: .
Tính tổng: .
Bài giải:
Từ (1) suy ra a, b, c ≤ 1. Trừ từng vế của (1) cho (2) ta có:
Vì a, b, c ≤ 1 nên .
Do đó: .
Từ đó ta có: . Suy ra: .
Bài 3: Cho x; y thoả mãn: . Hãy tính giá trị của biểu thức sau:
(Toán Tuổi Thơ số 14 – 2004)
Bài 4: Gọi a, b, c là độ dài 3 cạnh của một tam giác không phải là tam giác cân. Hãy so sánh giá trị tuyệt đối của các biểu thức P, Q sau đây:
(TTT số 12 - 2004)
Bài 5: Cho và với . Tính: .
(TTT số 11 – 2004)
Bài 6: Cho a + b + c = 0 và . Tính:
a)
Bạn đang xem tài liệu "Bồi dưỡng học sinh giỏi môn Toán Lớp 8 - Chuyên đề: Giá trị biểu thức - Nguyễn Hữu Hạnh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyên đề: giá trị biểu thức I. Một số dạng tính GTBT chung: Bài 1: Tính tổng , biết Bài giải: Ta có Do đó: (TTT số 9 - 2004) Tổng quát: . Bài 2: Cho 3 số a, b, c thoả mãn điều kiện: . Tính tổng: . Bài giải: Từ (1) suy ra a, b, c ≤ 1. Trừ từng vế của (1) cho (2) ta có: Vì a, b, c ≤ 1 nên . Do đó: . Từ đó ta có: . Suy ra: . Bài 3: Cho x; y thoả mãn: . Hãy tính giá trị của biểu thức sau: (Toán Tuổi Thơ số 14 – 2004) Bài 4: Gọi a, b, c là độ dài 3 cạnh của một tam giác không phải là tam giác cân. Hãy so sánh giá trị tuyệt đối của các biểu thức P, Q sau đây: (TTT số 12 - 2004) Bài 5: Cho và với . Tính: . (TTT số 11 – 2004) Bài 6: Cho a + b + c = 0 và . Tính: a) b) Bài 7: Cho . Tính giá trị của biểu thức: . BG: Vận dụng bài 2 ị P = 1 Bài 8: Cho . Tính a3 + b3 + c3 theo x, y, z. Bài 9: Cho các số a, b, c; x, y, z thoả mãn x = by + cz; y = ax + cz; z = ax + by; x + y + z≠0. Chứng minh: . Bài 10: Cho a, b, c là các số thực dương thoả mãn điều kiện: Tính a + b + c, biết rằng ab + bc + ca =9 CMR nếu c ≥ a; c ≥ b thì c ≥ a + b. Bài 11: Cho các số a, b, c thoả mãn: a + b + c = 0 (1) và . Tính . Bài 12: Biết 3a – b = 5. Tính giá trị của biểu thức: với 2a + 5 ≠ 0 và 2b – 5 ≠ 0. (Luyện kỷ năng. T8) (Còn nữa )
Tài liệu đính kèm:
 boi_duong_hoc_sinh_gioi_mon_toan_lop_8_chuyen_de_gia_tri_bie.doc
boi_duong_hoc_sinh_gioi_mon_toan_lop_8_chuyen_de_gia_tri_bie.doc





