Ôn tập hình học 8 - Chương I: Tứ giác

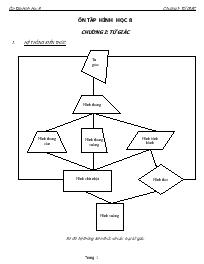
ÔN TÂP HÌNH HỌC 8
CHƯƠNG I: TỨ GIÁC
Hình chữ nhật
Hình thoi
Hình bình hành
Hình thang cân
Hình thang vuông
Hình vuông
Hình thang
Tứ giác
HỆ THỐNG KIẾN THỨC
Sơ đồ hệ thống kiến thức về các loại tứ giác
BÀI TẬP:
Bài 1:
Cho ΔABC vuông tại A, M là trung điểm BC, D là trung điểm AB, E là điểm đối xứng của M qua D.
C/m E đối xứng với M qua AB.
Tứ giác AEMC và AEBM là hình gì? Vì sao?
Cho AB=4 cm, tính chu vi tứ giác ARBM.
ΔABC cần có them điều kiện gì d963 tứ giác AEBM là hình vuông?
Bài 2:
Cho ΔABC cân tại A, AM là phân giác của góc A. Gọi I là trung điểm của AC, K là điểm đối xứng của M qua I.
C/m: AK ⁄⁄ MC.
Tứ giác AMCK là hình gì? Vì sao? 
Từ đó suy ra I là trung điểm của AC và MK
Nhận xét về đặc điểm của tứ giác ABMK.
Nếu tứ giác AKMC là hình vuông thì ΔABC cần phải có them điều kiện gì nữa không?
Bài 3:
Cho Δ ABC vuông tại A. Gọi D, E, F lần lượt theo thứ tự là trung điễm của AB, BC và CA.
Tứ giác ADEF là hình gì? Vì sao?
Gọi G là điểm đối xứng của E qua D. Tứ giác AECG là hình gì? Vì sao?
Gọi H là điểm đối xứng của E qua F. Tứ giác BCGH là hình gì? Vì sao?
D. ΔABC cần có them điều kiện gì để tứ giác AECG là hình vuông?
Bài 3:
Cho ΔABC. D thuộc BC. Vẽ DE//AC (E thuộc AB), DF//AB( F thuộc AC)
C/m tứ giác AFDE là hình bình hành.
Xác định vị trí điểm D để tứ giác AFDE lả hình thoi.
Bài 4:
Cho hình thang vuông ABCD (Â= D= 900) có DC= 2AB. Gọi H là hình chiếu cua3d trên AC, M là trung điểm của HC và N là trung điểm của HD.
Tứ giác ABMN là hình bình hành.
BM vuông góc với MD
Bài 5:
Cho hình bình hành ABCD có AB= 2BC. Gọi M, N lần lượt là trung điểm của AB và CD. Gọi E là giao điểm của AN và DM, F là giao điểm của BN và CM.
Tứ giác MENF là hình gì? Vì sao?
Hình bình hành ABCD cần có thêm điều kiện gì để tứ giác MENF là hình vuông? 
Bài 6:
Cho Hình vuông ABCD. Trên cạnh AB lấy điểm E. Tia phân giác của góc CDE cắt BC tại K. Gọi F là điểm trên tia đối của tia AB sao cho AF=CK. C/m:
ADF=CDK
 AE+CK=DE
Bài 7:
Cho ΔABC có Â< 900. Vẽ ở ngoài tam giác các hình vuông ABDE và ACFH.
C/m EC-BH và EC vuông góc với BH.
Gọi M, N lần lượt là tâm của các hình vuông ABDE và ACFH. Gọi I là trung điểm BC. 
C/m ΔIMN là tam giác vuông cân.
C/m đường cao AS của ΔABC đi qua trung điểm của đoạn thẳng EH.
 C/m AS, BF, CD đồng quy.
Bài 8:
Cho hình vuông ABCD.
Vẽ điểm E nằm bên trong hình vuông sao cho hai góc EDC và ECD đễu cùng bằng 150.
C/m ΔABE là tam giác đều
Bài 9:
Cho hình vuông ABCD có AB=1. Các điểm M, N lần lượt di động trên cạnh AB, AD sao cho AM+AN+MN=2. Dựng CH vuông góc với MN ( H thuộc MN) và R, S lần lượt là giao điểm của BD và CM, CN. C/m:
Số đo góc CHR là 450.
HC là tia phân giác góc của RHS.
BR, RS, SD lập thành ba cạnh của một tam giác.
Bài 10:
Cho hình thang ABCD (AB//CD) góc c nhỏ hơn góc D.
C/m AC> BD.
Vẽ AH vuông góc với Cd (H thuộc CD) và HC=5 (đvd). 
Tính độ dài đường trung bình của hình thang ABCD.
————————————————————————————————————