Giáo án tự chọn môn Toán Lớp 8 - Chủ đề Phương trình
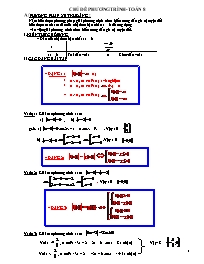
A/ PHƯƠNG PHÁP XÉT KHOẢNG :
+ Nắm biết được phương pháp giải phương trình chứa biến trong dấu giá trị tuyệt đối
+ biết được cách xét dấu của nhị thức bậc nhất ax + b để ứng dụng
vào việc giải phương trình chứa biến trong dấu giá trị tuyệt đối.
I.KIẾN THỨC BỔ SUNG
* Dấu của nhị thức bậc nhất ax + b
x
ax + b Trái dấu với a 0 Cùng dấu với a
II.CÁC DẠNG BÀI TẬP
Ví dụ 1: Giải các phương trình sau :
a) , b)
giải: a) 2x – 1 = 0 x = ½ . Vậy : S =
b) .Vậy : S =
Ví dụ 2: Giải các phương trình sau :
. Vậy : S =
Ví dụ 3: Giải các phương trình sau :
+ Với x , ta có Pt : 3x – 2 = 2x + 6 x = 8 ( nhận) Vậy : S =
+ Với x < ,="" ta="" có="" pt="" :="" 3x="" –="" 2="–2x" –="" 6="" x="-" 4/5="" (="" nhận)="">
Bạn đang xem 20 trang mẫu của tài liệu "Giáo án tự chọn môn Toán Lớp 8 - Chủ đề Phương trình", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHỦ ĐỀ PHƯƠNG TRÌNH -TOÁN 8 A/ PHƯƠNG PHÁP XÉT KHOẢNG : + Nắm biết được phương pháp giải phương trình chứa biến trong dấu giá trị tuyệt đối + biết được cách xét dấu của nhị thức bậc nhất ax + b để ứng dụng vào việc giải phương trình chứa biến trong dấu giá trị tuyệt đối. I.KIẾN THỨC BỔ SUNG * Dấu của nhị thức bậc nhất ax + b x ax + b Trái dấu với a 0 Cùng dấu với a II.CÁC DẠNG BÀI TẬP * DẠNG 1 : (1) a < 0 , ta có Pt (1) : vô nghiệm a = 0 , ta có Pt (1) f(x) = 0 a > 0 , ta có Pt (1) Ví dụ 1: Giải các phương trình sau : a) , b) giải: a) 2x – 1 = 0 x = ½ . Vậy : S = * DẠNG 2: b) .Vậy : S = Ví dụ 2: Giải các phương trình sau : . Vậy : S = * DẠNG 3: Ví dụ 3: Giải các phương trình sau : + Với x , ta có Pt : 3x – 2 = 2x + 6 x = 8 ( nhận) Vậy : S = + Với x < , ta có Pt : 3x – 2 = –2x – 6 x = - 4/5 ( nhận) * DẠNG 4: + Dùng bảng xét dấu các giá trị biến là nghiệm của các đa thức , để khử dấu giá trị tuyệt đối , rồi giải các Pt Ví dụ 4.1: Giải các phương trình sau : x 1/2 1 2x – 1 – 0 + + X - 1 – – 0 + + Bảng xét dấu : Với x < ½ , ta có Pt : 1 – 2x – 3( 1 – x ) = 1 x = 3 ( loại ) Với ½ x < 1 , ta có Pt : 2x – 1 – 3(1 – x ) = 1 x = 1 ( loại ) Với x 1 , ta có Pt : 2x – 1 – 3(x – 1 ) = 1 x = 1 ( nhận ) Vậy : S = Ví dụ 4.2: Giải các phương trình sau : ; ĐK : x 1 (2) ; ( vì ) * Nếu x > 2 thì Pt (2) +1 + - 1 = 2 = 1 x = 2 (loại) * Nếu 1 thì Pt (2) +1 + 1 - = 2 0.x = 0 , Pt vô số nghiệm Vậy Pt đã cho có nghiệm 1 + Cách khác : Sau khi biến đổi đến Pt (2) ta có thể viết : Chú ý bất đẳng thức với điều kiện xảy ra ” =” là A 0 . Vì thế 1 - 0 1 x 2 Kết hợp với ĐK ban đầu ta có 1 Ví dụ 4.2: c) Giai : Û Û . (2) + Nếu, (2)Þ Û: vô nghiệm. + Nếu : , (2)Þ ÛÛ. + Nếu : , (2)Þ ÛÛ, (loại). + Nếu ; , (2)Þ Û: vô nghiệm. Vậy phương trình đã cho có một nghiệm . III. BÀI TẬP ĐỀ NGHỊ Giải các phương trình sau : a) ; b) c) B/ PHƯƠNG PHÁP TỔNG CÁC SỐ KHÔNG ÂM + Sử dụng được tính chất tổng các số không âm để vận dụng vào việc giải phương trình. + Nhận dạng và biến đổi được các phương trình về dạng trên. I.CÁC DẠNG BÀI TẬP : * DẠNG 5 : A2 + B2 = 0 Ví dụ 5: Giải các phương trình sau : 2x2 + 2x + 1 = (*) Giải : ĐK : 4x + 1 0 x - ¼ (*) 4x2 + 4x + 2 = 2 4x2 + 4x + 1 – 2 +1 = 0 4x2 + ( - 1 )2 = 0 x = 0 ( nhận) . Vậy : S = Ví dụ 5’: Tìm các giá trị x, y, z biết : (1) + ĐK : x 2 ; y 3 ; z 5 (1) * DẠNG 6 : Ví dụ 6 : Giải các phương trình sau : (**) (**) x = 1 . Vậy : S = * DẠNG 7 : Ví dụ 7 : Giải các phương trình sau : x =1 . Vậy : S = II.BÀI TẬP ĐỀ NGHỊ Giải các phương trình sau : a) ; b) x + y + 4 = 2+ 4 ; c) x + y + z + 4 = ; d ) C. PHƯƠNG PHÁP ĐỐI LẬP VÀ BẤT ĐẲNG THỨC : + Sử dụng được tính chất đối lập ở hai vế của phương trình. + Ngoài những bất đẳng thức của các số không âm ở bài trước , cần nắm thêm và sử dụng một số bất đẳng thức quen thuộc như BĐT Cô Si; BĐT Svacxơ; BĐT về giá trị tuyệt đối vào việc giải phương trình. I/KIẾN THỨC CƠ BẢN 1_ Sử dụng tính chất tính chất đối nghịch giá trị của hai vế Pt : * DẠNG 8 : Ví dụ 8 : Giải các phương trình sau : a) Mà (VT) = , dấu”=” xảy ra khi (x + 1)2 = 0 x = -1 Và (VP) = 5 – (x + 1)2 5 , dấu “=” xảy ra khi (x + 1)2 = 0 x = -1 Do đó : (x + 1)2 = 0 x = -1 . Vậy : S = b) ; ĐK : (VT) : A = A2 = 2 + 2 (Áp dụng BĐT Cô Si 2) Do đó A 2 (VP) : B = = (x – 8 )2 + 2 2 Theo đề bài A = B nên A = B = 2 . Do đó x – 7 = 9 – x ; x = 8 (nhận) II. BÀI TẬP ĐỀ NGHỊ Ví dụ 18 : Giải các phương trình sau : a) b) c) 2_ Sử dụng bất đẳng thức CÔ-SI cho hai số không âm * DẠNG 9 : Với hai số a ,b không âm ta có : Dấu “=” xảy ra khi a = b Ví dụ 9.1 : Giải các phương trình sau : ĐK : Vì 5x3 + 3x2 + 3x – 2 = (x2 + x + 1) (5x – 2) Mà x2 + x + 1 = (x + ½)2 + ¾ > 0 nên có nghĩa khi 5x – 2 x 2/5 ( theo BĐT Cô-Si cho hai số không âm) Dấu “ = ” xảy ra khi x2 + x + 1 = 5x – 2 x2 – 4x + 3 = 0 (x – 1)(x – 3) = 0 x = 1 ; x = 3 . Vậy : S = Ví dụ 9.2 : Giải các phương trình sau : Áp dụng BĐT Cô-Si cho hai số không âm ta có :b Dấu “ = ” xảy ra khi x = 2 Mặt khác 3x2 – 12x +14 = 3(x2 – 4x + 4) + 2 = 3(x – 2)2 + 2 Dấu “ = ” xảy ra khi x – 2 = 0 x = 2 Vậy Pt có nghiệm duy nhất x = 2 3_ Sử dụng bất đẳng thức SVAC XƠ * DẠNG 10 : Dấu “=” xảy ra khi Ví dụ 10 : Giải các phương trình sau : ; ĐK : 2 x 10 Ta có (VT) = Nên : , dấu ‘=” xảy ra khi x = 6 Mà (VP) = , dấu ‘=” xảy ra khi x = 6 Vậy phương trình có một nghiệm duy nhất x = 6 4_ Sử dụng Bất đẳng thức về giá trị tuyệt đối : DẠNG 11 : Dấu “=” xảy ra khi A và B cùng dấu hay A.B 0 DẠNG 11’ : Dấu “=” xảy ra khi A 0 Ví dụ 11 : Giải các phương trình sau : Giải : Dấu “ =” xảy ra khi : (x – 2) (3 – x) 0 2 x 3 Vậy Pt đã cho có nghiệm là : 2 x 3 Ví dụ 11’ : Giải các phương trình sau : (1) Áp dụng BĐT dấu “=” xảy ra khi A 0 , ta có : (2) Do (1) nên phải xảy ra dấu “=” ở Pt (2) tức là nghiệm Pt CHỨNG TỎ PHƯƠNG TRÌNH VÔ NGHIỆM KHI CÓ 1 VẾ LUÔN NHỎ HƠN VẾ KIA 1) ; ĐK : x 1 Ta thấy vế phải lớn hơn vế trái , Pt 2) ; ĐK : 1 Ta thấy vế trái lớn hơn x , vế phải không lớn hơn x , Pt vô nghiệm 3) ĐK : x 1 , nên vế trái 2 ; vế phải 2 , suy ra hai vế bằng 2 , khi đó x = 1 II. BÀI TẬP ĐỀ NGHỊ Ví dụ 11 : Giải các phương trình sau : a) ; ĐK : x 0 , đưa về dạng Nghiệm : b) ; ĐK : x -2 , Đặt : đưa về dạng . Nghiệm : c) ; ĐK : x 2 , Đặt : đưa về dạng . Nghiệm : D. PHƯƠNG PHÁP ĐẶT ẨN PHỤ : + Biết thay thế một biểu thức chứa ẩn số trong phương trình bằng một ẩn số phụ để được một phương trình trung gian mà ta biết cách giải. + Biết tìm nghiệm số phụ từ đó suy ra nghiệm của phương trình. I/ NỘI DUNG : * DẠNG 12 : PT TRÙNG PHƯƠNG : ax4 + bx2 + c = 0 ( a 0 ) + Đặt : x2 = y 0 , ta có Pt : ay2 + by + c = 0 Ví dụ 12 : Giải các phương trình sau : x4 – x2 – 12 = 0 (1) Đặt : x2 = y 0 (1) y2 – y – 12 = 0 (y – 4)(y + 3) = 0 + Với y = 4 x2 = 4 x = 2 . Vậy : S = * DẠNG 13 : PT dạng : (x + a)(x + b)(x + c) (x + d) = m Với a + b = c + d + Đặt y = (x + a)(x + b) Ví dụ 13 : Giải các phương trình sau : (12x –1)(6x – 1)(4x – 1)(3x – 1) = 330 Giải : (12x –1)(12x – 2)(12x – 3)(12x – 4) = 330.2.3.4 (*) Đặt : y = 12x – 3 (*) (y + 2)(y +1)y (y -1) = 7920 (y2 + y - 2)(y2 + y) – 7920 = 0 (**) Đặt t = y2 + y -1 (**) (t – 1)(t + 1) = 7920 t2 = 7921 t = 89 + Với t = 89 thì ta có y2 + y – 90 = 0 + Với t = - 89 thì ta có y2 + y + 88 = 0 Pt vô nghiệm Vậy : S = * DẠNG 14 : PT dạng : (x + a)4 + (x + b)4 = k + Đặt : y = x + Ví dụ 14 : Giải các phương trình sau : ( x – 6)4 + (x – 8)4 = 16 (1) Giải : Đặt : y = x - 7 (1) ( y + 1)4 + (y – 1)4 = 16 khai triển rút gọn ta có : y4 + 6y2 – 7 = 0 (2) Giai Pt (2) ta được : x = 8 ; x = 6 * DẠNG 15 : Pt có hệ số đối xứng dạng : ax4 + bx3 cx2 + bx + a = 0 ( a 0 ) . + Vì x = 0 không phải nghiệm , nên ta chia 2 vế Pt cho x2 , Ta được Pt sau : a (x2 + ) + b ( x ) + c = 0 + Đặt : y = ( x ) , giải Pt ẩn y suy ra nghiệm x Ví dụ 15 : Giải các phương trình sau : x4 + 3x3 + 4x2 + 3x + 1 = 0 Giải : + Vì x = 0 không phải nghiệm , nên ta chia 2 vế Pt cho x2 , Ta được Pt sau : (x2 + ) + 3( x + ) + 4 = 0 (*) + Đặt : y = x + nên x2 + = y2 – 2 (*) y2 + 3y + 2 = 0 (y + 1)(y + 2) = 0 y = - 1 hoặc y = -2 + Với y = -1 ta có Pt : x + = -1 x2 + x + 1 = 0 Pt vô nghiệm . + Với y = -2 ta có Pt : x + = -2 x2 -2 x + 1 = 0 Pt có nghiệm x = -1 DẠNG 16 : Pt đẳng cấp bậc hai đối với u , v ( u, v phụ thuộc x ) Có dạng : au2 + buv + cv2 = 0 ( a 0 ) + xét v = 0 u = 0 + Xét v 0, chia hai vế cho v2 ta có Pt : Đặt y = ta có Pt bậc hai ẩn y : ay2 + by + c = 0 Ví dụ 16 : Giải các phương trình sau : (x2 – 3x – 1 )4 – 13x2 (x2 – 3x – 1)2 + 36x4 = 0 (*) Đặt : u = (x2 – 3x – 1)2 ; v = x2 (*) u2 – 13uv + 36v2 = 0 + Xét v = 0 u = 0 , ta có x + xét v 0 , chia hai cho v2 ta có Pt : Đặt y = ta có PTBh : y2 – 13y + 36 = 0 E-PHƯƠNG TRÌNH CHỨA CĂN THỨC ( HAY PT VÔ TỈ ) DẠNG 1 : + a < 0 , Pt vô nghiệm . + a = 0 , f(x) = 0 + a > ) _ Giải Pt - ĐK : f(x) 0 _ Bình phương hai vế _ Giải Pt , đối chiếu ĐK tìm nghiệm DẠNG 2: Ví dụ1. Giải phương trình: (1) Giải: (1) Û Vậy: phương trình đã cho có một nghiệm x = 3 DẠNG 3: (với a 0) Ví dụ 1. Giải phương trình: (1) Giải: (1) Û Với điều kiện x ≤ 8. Ta có: (1) Û |x – 2| = 8 – x – Nếu x < 2: (1) Þ 2 – x = 8 – x (vô nghiệm) – Nếu 2 ≤ x ≤ 8: (1) Þ x – 2 = 8 – x Û x = 5 ; HD: Đáp số: x = 5. DẠNG 4: Ví dụ : Giải các phương trình sau : a) ; Giải Pt : 4x2 – 29x + 52 = 0 được x = 4 (nh) ; x = 13/4 (loại) b) DẠNG 4.1: Ví dụ 1: Giải phương trình: (2) Giải. Với điều kiện x ≥ 2. Ta có: (2) Û Û ( bình phương 2 vế ) Û Û Vậy: phương trình đã cho có một nghiệm x = 6 DẠNG 4.2: Ví dụ. Giải phương trình: (3) Giải: Với điều kiện 7 ≤ x ≤ 12. Ta có: (3) Û Û ( bình phương 2 vế ) Û Û 4(19x – x2 – 84) = x2 – 8x + 16 Û 76x – 4x2 – 336 – x2 + 8x – 16 = 0 Û 5x2 – 84x + 352 = 0 Û x1 = ; x2 = 8 Vậy: phương trình đã cho có hai nghiệm x1 = ; x2 = 8 DẠNG 4.3: Ví dụ1. Giải phương trình: (4) Giải: Với điều kiện x ≥ 4. Ta có: (4) Û Û Û Û Û 45 + 14x + 14 = 0 Với x ≥ 4 Þ vế trái của phương trình luôn là một số dương Þ phương trình vô nghiệm Ví dụ 2. Giải phương trình (2) Giải: (2) Û Û Đặt y = (y ≥ 0) Þ phương trình đã cho trở thành: – Nếu 0 ≤ y < 1: y + 1 + 3 – y = 2 – 2y Û y = –1 (loại) – Nếu 1 ≤ y ≤ 3: y + 1 + 3 – y = 2y – 2 Û y = 3 – Nếu y > 3: y + 1 + y – 3 = 2y – 2 (vô nghiệm) Với y = 3 Û x + 1 = 9 Û x = 8 Vậy: phương trình đã cho có một nghiệm là x = 8 BÀI TẬP : Giải các phương trình sau : 1/ ; KQ : S = 3/ ; KQ : S = 1. Phương pháp nâng lên lũy thừa a) Dạng 2: Û Ví dụ. Giải phương trình: (1) Giải: (1) Û Vậy: phương trình đã cho có một nghiệm x = 3 b) Dạng 2: c) Dạng 3: d) Dạng 4: 2/ ; KQ : S = F. PHƯƠNG TRÌNH CÓ NHIỀU DẤU CĂN THỨC : PP chính : Điều kiện cho Pt có nghĩa , chuyển vế cho hợp lí , bình phương hai vế , đối chiếu điều kiện chọn nghiệm . 1) ; ĐK1 : x _Chuyển vế ( bớt dấu - ) ,ta có : _ Bình phương hai vế rút gọn được : 2 – 7x = Đến đây có hai cách giải : Cách 1: ĐK2 : 2 – 7x 0 _ Bình phương hai vế rút gọn được : 11x2 – 24x + 4 = 0 (11x – 2)(x – 2) = 0 x1 = 2/11 (loại ) ; x2 = 2 ( loại ) . Vậy Pt vô nghiệm Cách 2 : ta có ĐK2 : 2 – 7x 0 x 2/7 trái với ĐK1 : x Vậy Pt vô nghiệm 2) ĐK: x 4 ; bình phương hai vế ta có KQ : S ... số (tìm một nghiệm, chứng minh nghiệm đó là duy nhất) Ví dụ 1. Giải phương trình: Giải: điều kiện x ≥ Dễ thấy x = 2 là một nghiệm của phương trình – Nếu : VT = . Mà: VP > – Nếu x > 2: VP = 2x2 + > 2.22 + = . VT < Vậy: phương trình đã cho có một nghiệm duy nhất là x = 2 Ví dụ 2. Giải phương trình: Giải: Thử với x = 2. Ta có: (1) Û Nếu x > 2: VT < VP Nếu x VP Vậy: x = 2 là nghiệm duy nhất của phương trình Ví dụ 3. Giải phương trình: Giải: ĐK: x < 2. Bằng cách thử, ta thấy x = là nghiệm của phương trình. Ta cần chứng minh đó là nghiệm duy nhất. Thật vậy: Với x < : và Þ . Tương tự với < x < 2: Ví dụ 4. Giải phương trình: (1) Giải: (1) Nếu 3x = –(2x + 1) Û x = thì các biểu thức trong căn ở hai vế bằng nhau. Vậy x = là một nghiệm của phương trình. Hơn nữa nghiệm của (1) nằm trong khoảng . Ta chứng minh đó là nghiệm duy nhất. Với : 3x < –2x – 1 < 0 Þ (3x)2 > (2x + 1)2 Þ Suy ra: Þ (1) không có nghiệm trong khoảng này. Chứng minh tương tự, ta cũng đi đến kết luận (1) không có nghiệm khi d) Sử dụng điều kiện xảy ra dấu “=” ở bất đẳng thức không chặt Ví dụ. Giải phương trình Giải: điều kiện Áp dụng bất đẳng thức với ab > 0 Với điều kiện . Nên: . Dấu “=” xảy ra Û Û BÀI TẬP 1. Phương trình chứa và . Đặt suy ra phương trình bậc hai theo . 2. Phương trình chứa nhiều căn thức. Đặt điều kiện để căn thức có nghĩa. Nâng lũy thừa nhiều lần để khử dần các căn. Giải phương trình so với điều kiện suy ra nghiệm. 3. Dùng ẩn số phụ. Đặt là các căn thức, suy ra phương trình bậc 2, bậc 3,theo . Hoặc đặt và là các căn thức, suy ra hệ phương trình theo và . I.2. Các ví dụ minh họa Ví dụ 1. Giải phương trình: . Đs: . Ví dụ 2. Giải phương trình: . Đs: . Ví dụ 3. Giải phương trình: . Đs: . Ví dụ 4. Giải phương trình: . Đs: . Ví dụ 5. Giải phương trình: . Đs: . Ví dụ 6. Giải phương trình: . Đs: . Ví dụ 7. Giải phương trình: . Đs: . I.3. Bài tập Bài 1. Giải phương trình: . Đs: . Bài 2. Giải phương trình: . Đs: . Bài 3. Giải phương trình: . Đs: . Bài 4. Giải phương trình: . Đs: . Bài 5. Giải phương trình: . Đs: . Bài 6. Giải phương trình: . Đs: . Bài 7. Giải phương trình: . Đs: . Bài 8. Giải phương trình: . Đs: . Bài 9. Giải phương trình: . Đs: . Bài 10. Giải phương trình: . Đs: . Bài 11. Giải phương trình: . Đs: . Bài 12. Giải phương trình: . Đs: . Bài 13. Giải phương trình: . Đs: . Bài 14. Giải phương trình: . Đs: . Bài 15. Giải phương trình: . Đs: . Bài 16. Giải phương trình: . Đs: . Bài 17. Giải phương trình: . Đs: . Bài 18. Giải phương trình: . Đs: . Bài 19. Giải phương trình: . Đs: . Bài 20. Giải phương trình: . Đs: . Bài 21. Giải phương trình: . Đs: . Bài 22. Giải phương trình: . Đs: . Bài 23. Giải phương trình: . Đs: . Bài 24. Giải phương trình: . Đs: . Bài 25. Giải phương trình: . Đs: . Bài 26. Giải phương trình: . Đs: . Bài 27. Giải phương trình: . Đs: . Bài 28. Giải phương trình: . Đs: . Bài 29. Giải phương trình: . Đs: . Bài 30. Giải phương trình: . Đs: . Bài 31. Giải phương trình: . Đs: . Bài 32. Giải phương trình: . Đs: . Bài 33. Giải phương trình: . Đs: . Bài 34. Giải phương trình: . Đs: . Bài 35. Giải phương trình: . Đs: . Bài 36. Giải phương trình: . Đs: . Bài 37. Giải phương trình: . Đs: . Bài 38. Giải phương trình: . Đs: . Bài 39. Giải phương trình: . Đs: . Bài 40. Giải phương trình: . Đs: . Bài 41. Giải phương trình: . Đs: . Bài 42. . Đs: . Bài 43. Giải phương trình: . Đs: . Bài 44. Giải phương trình: . Đs: . Bài 45. Giải phương trình: . Đs: . Bài 46. Giải phương trình: . Đs: . Bài 47. Giải phương trình: . Đs: . Bài 48. Giải phương trình: . Đs: . Bài 49. Giải phương trình: . Đs: . Bài 50. Giải phương trình: . Đs: . Bài 51. Giải phương trình: . Đs: . Bài 52. Giải phương trình: . Đs: . Bài 53. Giải phương trình: . Đs: . Bài 54. Giải phương trình: . Đs: . II. Định m để phương trình chứa căn thức có nghiệm, có nghiệm duy nhất, giải và biện luận phương trình II.1. Kiến thức cần nhớ Định m để phương trình có nghiệm . Đặt ẩn số phụ: , tìm điều kiện cho ẩn số phụ của . Chuyển điều kiện thành . Biến đổi phương trình thành phương trình với . Để phương trình có nghiệm phương trình có nghiệm Đường thẳng có điểm chung với đồ thị trên . Từ bảng biến thiên điều kiện của . Cách khác: (nếu tham số bậc hai) Phương trình có nghiệm phương trình có nghiệm . có 1 trong hai nghiệm thuộc hoặc có cả hai nghiệm thuộc . Định m để phương trình có nghiệm duy nhất . Điều kiện cần: Giả sử phương trình có nghiệm . Dựa vào tính đối xứng, hàm số chẵnsuy ra cũng là nghiệm của phương trình. Do đó phương trình có nghiệm duy nhất khi . Thay vào phương trình . Điều kiện đủ: Thay giá trị vừa tìm được vào phương trình, giải phương trình có nghiệm duy nhất. Vậy phương trình có nghiệm duy nhất. Cách khác: Đặt ẩn số phụ . Tìm điều kiện . Biến đổi về dạng . Tính , lập bảng biến thiên trên . có nghiệm duy nhất trên đường thẳng chỉ có một điểm chung với . GIẢI VÀ BIỆN LUẬN PHƯƠNG TRÌNH . Đặt ẩn số phụ . Biến đổi thành phương trình đại số theo . Tìm điều kiện của ẩn số phụ . Biện luận phương trình theo (phương pháp đại số hoặc phương pháp đồ thị). II.2. Ví dụ minh họa Ví dụ 1. Định để phương trình: có nghiệm. Đs: . Ví dụ 2. Tìm để phương trình: có nghiệm. Đs: . Ví dụ 3. Tìm để phương trình: có nghiệm duy nhất. Đs: . Ví dụ 4. Giải và biện luận phương trình: . Đs: Nếu thì phương trình vô nghiệm. Nếu thì phương trình có nghiệm là . Nếu thì phương trình có nghiệm là . Ví dụ 5. Giải và biện luận phương trình: . Đs: Nếu thì phương trình có 2 nghiệm. Nếu thì phương trình có 1 nghiệm. Nếu thì phương trình vô nghiệm. II.3. Bài tập Bài 1. Cho phương trình: . Giải phương trình với . Tìm để phương trình có nghiệm. Đs: Bài 2. Cho phương trình: . Giải phương trình với . Tìm để phương trình có nghiệm. Đs: Bài 3. Tìm để phương trình: có nghiệm. Đs: . Bài 4. Tìm để phương trình: có nghiệm. Đs: . Bài 5. Tìm để phương trình: có nghiệm. Đs: . Bài 6. Tìm để phương trình: có nghiệm. Đs: . Bài 7. Tìm để phương trình: có nghiệm duy nhất. Đs: . Bài 8. Tìm để phương trình: có nghiệm. Đs: hoặc . Bài 9. Tìm để phương trình: có nghiệm. Đs: . Bài 10. Tìm để phương trình: có nghiệm duy nhất. Đs: . Bài 11. Tìm để phương trình: có nghiệm duy nhất. Đs: Không có giá trị nào của thỏa mãn điều kiện bài toán. Bài 12. Tìm để phương trình: có nghiệm. Đs: . Bài 13. Tìm để phương trình: có nghiệm duy nhất. Đs: . Bài 14. Giải và biện luận phương trình: . Đs: Nếu thì phương trình vô nghiệm. Nếu thì phương trình có 2 nghiệm. Bài 15. Giải và biện luận phương trình: . Đs: Nếu thì phương trình vô nghiệm. Nếu thì phương trình có nghiệm là . Nếu thì phương trình có nghiệm là . Bài 16. Giải và biện luận phương trình: . Đs: Nếu thì phương trình có nghiệm . Nếu thì phương trình vô nghiệm. Bài 17. Giải và biện luận phương trình: . Đs: Nếu thì phương trình có nghiệm là . Nếu thì phương trình vô nghiệm. Bài 18. Giải và biện luận phương trình: . Đs: Nếu thì phương trình vô nghiệm. Nếu thì phương trình có 2 nghiệm: BÀI TẬP III- Dïng Èn phô ®Ó gi¶i ph¬ng tr×nh v« tû (HÖ ph¬ng tr×nh) 1. ChuyÓn hÖ ph¬ng tr×nh v« tû vÒ hÖ ph¬ng tr×nh h÷u tû Bµi 1: Gi¶i ph¬ng tr×nh : (1) Gi¶i: §K §Æt: Tõ ®ã ph¬ng tr×nh (1) chuyÓn thµnh hÖ ph¬ng tr×nh Trõ tõng vÕ (2) vµ (3) ta ®îc: , X¶y ra 2 trêng hîp a) hay , thay vµo (2) ta cã: Gi¶i ra ta ®îc (NhËn) ; (Lo¹i) v× b) hay , thay vµo (2) ta cã: Gi¶i ra ta ®îc: VËy ph¬ng tr×nh ®· cho cã 2 nghiÖm: vµ Bµi 2: Gi¶i ph¬ng tr×nh : §Æt: ; KÕt hîp víi (1) ta ®îc hÖ: (2) Tõ hÖ (2) suy ra : Tõ hÖ (2) b»ng c¸ch céng ta ®îc: VËy tõ (3) ta cã thay vµo (1) ta ®îc Gi¶i ph¬ng tr×nh trªn ta ®îc : thay vµo (Lo¹i) ; VËy ph¬ng tr×nh cã nghiÖm duy nhÊt Bµi 3: Gi¶i ph¬ng tr×nh : Gi¶I : §Æt Tõ ®ã ph¬ng tr×nh (1) chuyÓn thµnh hÖ ph¬ng tr×nh: BiÕn ®æi ph¬ng tr×nh (3) thµnh: KÕt hîp víi (2) ta ®îc Gi¶i hÖ ta ®îc nghiÖm Tõ ®ã vµ lµ nghiÖm cña ph¬ng tr×nh (1) Bµi 4: Gi¶i ph¬ng tr×nh : ; §K: Gi¶I : §Æt Ph¬ng trinh (1) chuyÓn thµnh hÖ PT: Tõ (2) ta cã: ; thay vµo (3) ta ®îc Tõ ®ã ta cã: Bµi 5: Gi¶i ph¬ng tr×nh : Gi¶i : §K: ; §Æt Tõ ph¬ng tr×nh (1) ta cã: Ta cã: ViÖc gi¶i ph¬ng tr×nh (1) chuyÓn vÒ gi¶i HPT h÷u tû sau: Gi¶i hÖ nµy ®îc ; Tõ ®ã ta t×m ®îc Bµi 6: Gi¶i ph¬ng tr×nh ; Gi¶i: §K: §Æt ViÖc gi¶i PT (1) chuyÓn vÒ gi¶i hÖ PT : Gi¶i hÖ trªn ta ®îc Tõ ®ã suy ra: Bµi tËp t¬ng tù: Gi¶i c¸c ph¬ng tr×nh sau: 2) Dïng Èn phô ®Ó ®a ph¬ng tr×nh v« tû vÒ ph¬ng tr×nh bËc hai: Bµi 1: Gi¶i ph¬ng tr×nh: (§Ò thi vµo chuyªn to¸n Lª Quý §«n - §N) §Æt ; Ph¬ng tr×nh ®· cho Ph¬ng tr×nh cã 2 nghiÖm lµ Do ®ã ph¬ng tr×nh ®· cho cã 2 nghiÖm Bµi 2: (§Ò thi vµo c¸c líp chuyªn KHTN - NguyÔn Tr·i - 2000) Gi¶i ph¬ng tr×nh: Gi¶i: §K: ; §Æt: Thay vµo ph¬ng tr×nh ban ®Çu ta ®îc Gi¶i ph¬ng tr×nh (*) ta ®îc: (Lo¹i) ; Víi ta ®îc KL: ph¬ng tr×nh cã nghiÖm duy nhÊt Bµi 3: (§Ò thi vµo NguyÔn Tr·i-2003) Gi¶i ph¬ng tr×nh ; Gi¶i: §K: ; ®Æt: Thay vµo ph¬ng tr×nh ban ®Çu ta ®îc : §K: Víi . VËy ph¬ng tr×nh cã nghiÖm duy nhÊt Bµi 4: (§Ò thi vµo chuyªn To¸n - TrÇn Phó) Gi¶i PT: Gi¶I : ®k: ; §Æt: Ph¬ng tr×nh trë thµnh: Víi ta cã ; Gi¶i ph¬ng tr×nh nµy ta ®îc Bµi tËp t¬ng tù: Bµi 1: Gi¶i ph¬ng tr×nh HD: §Æt Bµi 2: (§Ò thi vµo chuyªn To¸n - §H KHTN) Gi¶i ph¬ng tr×nh: Bµi 3: (§Ò thi chuyªn To¸n - §H KHTN) Gi¶i ph¬ng tr×nh: 3. Dïng Èn phô ®Ó gi¶i c¸c bµi to¸n kh¸c Khi kh«ng thÓ ®Æt Èn phô ®a vÒ hÖ ph¬ng tr×nh h÷u tû hoÆc ph¬ng tr×nh bËc hai ta lµm thÕ nµo? C©u tr¶ lêi lµ: ta thö kÕt hîp 2 ph¬ng ph¸p ®ã xem cã gi¶i quyÕt ®îc vÇn ®Ò kh«ng ! VÝ dô 1: (§Ò thi hs giái tØnh 2002) Trõ 2 vÕ cña ph¬ng tr×nh ta ®îc Tõ ®ã hÖ trë thµnh §Æt: ; Ta cã => lµ nghiÖm cña ph¬ng tr×nh: hoÆc vµ HoÆc vµ ; Kl: HÖ cã 2 nghiÖm VÝ dô 2: ( Thi vµo chuyªn To¸n TrÇn Phó - 2004) Gi¶i ph¬ng tr×nh: Gi¶I : §Æt Ph¬ng tr×nh ®· cho trë thµnh: ; Do chia c¶ hai vÕ cho ta ®îc Gi¶i ph¬ng tr×nh bËc hai theo Èn ta ®îc: Víi (HÖ v« nghiÖm) HÖ nµy cã 2 nghiÖm: §èi víi mét sè bµi to¸n ngoµi viÖc Èn phô ta cßn ph¶i kÕt hîp víi ph¬ng ph¸p nhËn xÐt ®¸nh gi¸. VD1: Gi¶i ph¬ng tr×nh: Gi¶i: ®k: ; ®Æt: Th× ph¬ng tr×nh trë thµnh: (*) NÕu ; Hay v« lý (*) NÕu hay v« lý . VËy , do ®ã ta ®îc: VËy ph¬ng tr×nh cã nghiÖm Bµi tËp tæng qu¸t: Ph¬ng tr×nh.
Tài liệu đính kèm:
 giao_an_tu_chon_mon_toan_lop_8_chu_de_phuong_trinh.doc
giao_an_tu_chon_mon_toan_lop_8_chu_de_phuong_trinh.doc





