Giáo án phụ đạo môn Toán Lớp 8 - Buổi 6 - Nguyễn Hữu Vinh
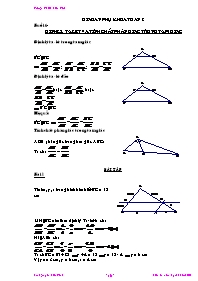
Định lý ta-let trong tam giác
BC//BC
Định lý ta-let đảo
hoặc hoặc
BC//BC
Hệ quả:
BC//BC
Tính chất phân giác trong tam giác
AD là phân giác trong tam giác ABC:
Ta có:
Bạn đang xem tài liệu "Giáo án phụ đạo môn Toán Lớp 8 - Buổi 6 - Nguyễn Hữu Vinh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Giáo án phụ khoá toán 8 Buổi 6. Định lý talet và tính chất phân giác trong tam giác Định lý ta-let trong tam giác B’C’//BC Định lý ta-let đảo hoặc hoặc B’C’//BC Hệ quả: B’C’//BC Tính chất phân giác trong tam giác AD là phân giác trong tam giác ABC: Ta có: Bài tập Bài 1 Tính x, y, z trong hình bên biết BC = 12 cm MN//BC nên theo định lý Ta-let ta có: NI//AB ta có: Ta có BC = BI + CI y + 4 = 12 y = 12 - 4 y = 8 cm Vậy x = 3 cm, y = 8 cm, z = 4 cm Bài 2 Cho tam giác ABC có trọng tâm G. Lấy các điểm M và N lần lượt thuộc các cạnh AB, AC sao cho AM = 2 MB, AN = AC. Chứng minh 3 điểm M, N, G thẳng hàng. Theo giả thiết ta có: ; Vì G là trong tâm tam giác => G là trong tâm tam giác nên ta cũng có: Vì MG//BC và NG//BC nên => M, N, G là ba điểm thẳng hàng. Bài 3 Cho tam giác ABC có BC = 9 cm. Lấy các điểm M,N trên AB sao cho: AM = MN = NB, từ M và N kẻ các đường thẳng song song với BC cắt cạnh AC theo thứ tự tại D và E. tính độ dài các đoạn DM và EN. Vì MD//BC nên theo Hệ quả của định lý Ta-let ta có: cm NE//BC nên ta cũng có: Vậy MD = 3cm, NE = 6 cm Bài 4 Cho tam giác ABC. Từ điểm N trên AC kẻ các đường thẳng song song với ácc cạnh BC và AB theo thứ tự tại I và M. Chứng minh rằng Bài làm Ta thấy MNIB là hình bình hành nên MN = BI, BM = NI Từ đó ta có : (1) Vì IN//BA nên theo Hệ quả Đ/l Ta-let ta có (2) Từ (1) và (2) ta suy ra Vậy Bài 5. Cho tam giác ABC. Một đường thẳng song song với BC cắt cạnh AB, AC theo thứ tự tại D và E. Biết BD = 9cm, CE = 12 cm, DE = 14 cm. Điểm M nằm trên đoạn DE sao cho DM = 6cm. chứng minh rằng AM là tia phân giác của góc A Theo giả thiết ta có: Mặt khác do DE//BC nên ta có: Từ (1) và (2) suy ra : AM là tia phân giác của góc A Ngày14 /2/09 Xác nhận của chuyên môn
Tài liệu đính kèm:
 giao_an_phu_dao_mon_toan_lop_8_buoi_6_nguyen_huu_vinh.doc
giao_an_phu_dao_mon_toan_lop_8_buoi_6_nguyen_huu_vinh.doc





