Giáo án Hình học 9 - Chương III
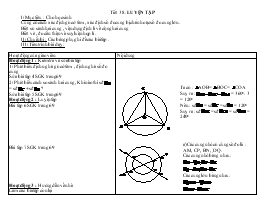
I/ Mục tiêu : Cho học sinh
Củng cố cách xác định góc ở tâm , xác định số đo cung bị chắn hoặc số đo cung lớn .
Biết só sánh hai cung , vận dụng định lí về cộng hai cung
Biết vẽ , đo cẩn thận và suy luận hợp lí .
II/ Chuẩn bị : Các bảng phụ ghi đề các bài tập .
III/ Tiến trình bài dạy :
Bạn đang xem 20 trang mẫu của tài liệu "Giáo án Hình học 9 - Chương III", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Tiết 38 : LUYỆN TẬP I/ Mục tiêu : Cho học sinh Củng cố cách xác định góc ở tâm , xác định số đo cung bị chắn hoặc số đo cung lớn . Biết só sánh hai cung , vận dụng định lí về cộng hai cung Biết vẽ , đo cẩn thận và suy luận hợp lí . II/ Chuẩn bị : Các bảng phụ ghi đề các bài tập . III/ Tiến trình bài dạy : Hoạt động của giáo viên Nội dung Hoạt động 1 : Kiểm tra và sửa bài tập 1/ Phát biểu định nghĩa góc ở tâm , định nghĩa số đo cung Sửa bài tập 4 SGK trang 69 2/ Phát biểu cách so sánh hai cung , Khi nào thì sđ = sđ + sđ ? Sửa bài tập 5 SGK trang 69 Hoạt động 2 : Luyện tập Bài tập 6 SGK trang 69 Bài tập 7 SGK trang 69 Hoạt động 3 : Hướng dẫn về nhà Làm các bài tập còn lại Xem trước bài liên hệ giữa cung và dây . Ta có : AOB = BOC = COA Suy ra : = 3600 : 3 = 1200 Nên : sđ = sđ =sđ = 1200 Suy ra : sđ = sđ = sđ = 2400 a)Các cung nhỏ có cùng số đo là : AM , CP , BN , DQ . Các cung nhỏ bằng nhau : Các cung lớn bằng nhau : Tiết 39 : LIÊN HỆ GIỮA CUNG VÀ DÂY I/ Mục tiêu : Cho học sinh Hiểu và sử dụng các cụm từ “ cung căng dây “ và “ dây căng cung “ , phát biểu và chứng minh được các định lí . Bước đầu vận dụng được hai định lí vào bài tập . II/ Chuẩn bị : Các bảng phụ ghi các định lí và hình vẽ . III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Định lí 1 Treo bảng phụ có hình vẽ Giới thiệu thuật ngữ “ cung căng dây “ và “ dây căng cung “ Nêu định lí Cho làm nhóm ? 1 ( chia làm hai nhóm , mỗi nhóm chứng minh một phần ) Hoạt động 2 : Định lí 2 Nêu định lí Cho làm ? 2 Hoạt động 3 : Củng cố Làm bài tập 10 , 13 , 14 SGK trang 71 , 72 Từ bài tập 13 , 14 rút ra hai tính chất Hoạt động 4 : Hướng dẫn về nhà Làm các bài tập còn lại , học thuôc các định lí và các tính chất vừa được suy ra . Ta có : = Suy ra : sđ = sđ Nên : Mà OA = OC OB = OD Nên : AOB = COD ( c . g . c ) Do đó suy ra : AB = CD b) Ta có : à OA = OC OB = OD AB = CD Nên : AOB = COD ( c . c . c ) Suy ra : Nên sđ = sđ Hay : = Để chỉ mối liên hệ giữa cung và dây người ta thường nói : “ cung căng dây “ và “ dây căng cung “ Như vậy mỗi dây căng hai cung riêng biệt Quy ước : Ta chỉ xét dây căng cung nhỏ Ví dụ : Dây AB căng cung AmB 1 / Định lí 1 : SGK Chứng minh : Học sinh tự ghi chứng minh Định lí 2 : SGK Tiết 40 : GÓC NỘI TIẾP I / Mục tiêu yêu cầu : Cho học sinh Nhận biết được những góc nội tiếp trên một đường tròn và phát biểu được định nghĩa về góc nội tiếp Phát biểu và chứng minh được định lí về số đo của góca nội tiếp . Nhận biết và chứng minh được các hệ quả của định lí trên . Biết cách phân chia trường hợp . II/ Chuẩn bị : Bảng phụ các hình vẽ và câu hỏi III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Kiểm tra bài cũ Cung bị chắn là cung có vị trí như thế nào đối với góc ? Hoạt động 2 : Định nghĩa Treo bảng phụ có hình 13 Góc ABC ở hình 13 gọi là góc nội tiếp . Vậy góc nội tiếp là gì ? Cung bị chắn là cung nào ? Cung bị chắn là những loại cung nào ? Trả lời ?1 Hoạt động 2 : Định lí Phát biểu định lí . Treo bảng phụ có hình 16 , 17 , 18 SGK trang 74 Xác định vị trí của tâm đường tròn đối với góc nội tiếp BAC trong mỗi trường hợp . Ta sẽ chứng minh định lí đối với trường hợp 1 Điều phải chứng minh ? sđ bằng gì ? Ta cần tìm gì ? Góc BOC là góc ngoài của tam giác AOC ta có gì ? từ đó suy ra điều phải tìm . Đối với trường hợp 2 hãy chứng minh bằng cách điền vào chỗ ( ... ) Vì O nằm bên trong góc BAC nên tia AO nằm giữa hai tia AB , AC . Ta có : = ... Sđ + sđ = ... Mà = ... = ... Suy ra = ... = ... = ... Trương hợp 3 tương tự về nhà chứng minh Hoạt động 4 : Hệ quả . Cho học sinh đọc hệ quả . Làm ? 3 Hoạt động 5 : Luyện tập Bài tập 15 , 17 SGK trang 75 Hoạt động 6 : Hướng dẫn về nhà Học thuộc định nghĩa , định lí , hệ quả góc nội tiếp . Làm bài tập 16 , 18 SGK trang 75 Cung bị chắn là cung nằm trong góc . Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh của nó chứa hai dây cung của đường tròn đó . Cung BC là cung bị chắn . Cung bị chắn là cung nhỏ hoặc cung lớn , cung nửa đường tròn . Tâm đường tròn nằm trên một cạnh của góc . Tâm đường tròn nằm bên trong góc . Tâm đường tròn nằm bên ngoài góc . Vì O nằm bên trong góc BAC nên tia AO nằm giữa hai tia AB , AC . Ta có : = Sđ + sđ = sđ Mà = sđ = sđ Suy ra = = sđ + sđ = ( sđ + sđ ) = sđ 1/ Định nghĩa : Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh của nó chứa hai dây cung của đường tròn đó . Cung nằm bên trong góc gọi là cung bị chắn . BAC là góc nội tiếp chắn cung BC 2 / Định lí : SGK trang 73 Chứng minh : Học sinh tự ghi . 3/ Hệ quả : SGK trang 74 a) b) c) d ) = 900 Tiết 41 : LUYỆN TẬP I / Mục tiêu yêu cầu : Cho học sinh Nắm vững và ứng dung định nghĩa , tính chất của góc nội tiếp vào bài tập . Rèn luyện kĩ năng vẽ hinh và chứng minh , áp dụng vào bài toán thực tế . II/ Chuẩn bị : Bảng phụ các hình vẽ và câu hỏi III/ Tiến trình bài dạy : Hoạt động của giáo viên Nội dung Hoạt động 1 : Kiểm tra và sửa bài tập 1/ Phát biểu định nghĩa , định lí góc nội tiếp Sửa bài tập 16 SGK trang 75 2/ Phát biểu hệ quả , trả lời bài tập 18 SGK trang 75 Hoạt động 2 : Luyện tập Bài tập 19 SGK trang 75 SH AB SH là đường cao của SAB H là trực tâm của SAB AN SB BM SA = 900 = 900 Bài tập 20 SGK trang 76 C, B , D thẳng hàng = 1800 + = 1800 = 900 = 900 Bài tập 23 SGK trang 76 MA . MB = MC . MD MAD = MCD ( chung ) Hoạt động 3 : Hướng dẫn về nhà Làm các bài tập còn lại , xem trước bài “ Góc tạo bởi tia tiếp tuyến và dây cung . Bài tập 19 SGK trang 75 Ta có : = 900 ( Góc nội tiếp chắn nửa đường tròn ) Suy ra : AN SB Và : = 900 ( Góc nội tiếp chắn nửa đường tròn ) Suy ra : BM SA Nên : H là trực tâm của SAB Suy ra : SH là đường cao của SAB Nên : SH AB Bài tập 20 SGK trang 76 Ta có : = 900 ( Góc nội tiếp chắn nửa đường tròn ) Và = 900 ( Góc nội tiếp chắn nửa đường tròn ) Suy ra : + = 1800 Nên = 1800 Vậy : C, B , D thẳng hàng Bài tập 23 SGK trang 76 Ta có : ( góc chung ) Và : ( Góc nội tiếp cùng chắn cung ) Nên : MAD = MCD ( g . g ) Suy ra : Suy ra : MA . MB = MC . MD Tiết 42 : GÓC TẠO BỞI TIA TIẾP TUYẾN VÀ DÂY CUNG I / Mục tiêu yêu cầu : Cho học sinh Nhận biết góc tạo bởi tia tiếp tuyến và dây cung , phát biểu và chứng minh được định lí về số đo của góc tạo bởi tia tiếp tuyến và dây cung , phát biểu và chứng minh định lí đảo . Rèn luyện kĩ năng phân chia trường hợp để chứng minh . II/ Chuẩn bị : Bảng phụ các hình vẽ và câu hỏi III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Kiểm tra Phát biểu định lí về số đo góc nội tiếp . Hoạt động 2 : Khái niệm góc tạo bởi tia tiếp tuyến và dây cung . Treo bảng phụ có hình 22 SGK trang 77 Ax , Ay gọi là tia tiếp tuyến . gọi là góc tạo bởi tia tiếp tuyến và dây cung . Vậy góc tạo bởi tia tiếp tuyến và dây cung là gì ? chắn những cung nào ? Làm ? 1 Hoạt động 3 : Định lí Làm ? 2 Nêu định lí Điều phải chứng minh ? Qua hình vẽ ở ? 2 Có mấy trường hợp xãy ra ? là các trường hợp nào ? Xét trường hợp tâm đường tròn nằm trên cạnh chứa dây cung . = ? sđ = ? Xét trường hợp tâm đường tròn năm bên ngoài góc . Hướng dẫn học sinh đi đến sơ đồ sau : sđ sđ= ABC vuông tại A Trường hợp tâm đường tròn nằm bên trong góc ( học sinh về nhà chướng minh ) Hoạt đông 4 : Hệ quả Cho làm ? 3 suy ra hệ quả Hoạt động 5 : Luyện tập củng cố Bài tập 30 SGK trang 79 Hoạt động 6 : Hướng dẫn về nhà Học thuộc định nghĩa , định lí và hệ quả . Làm các bài tập 27 , 28 , 29 SGK trang 79 Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn , một cạnh là tia tiếp tuyến , một cạnh chứa một dây cung của đường tròn . chắn cung nhỏ AB , chắn cung lớn AB . 1/ Khái niệm góc tạo bởi tia tiếp tuyến và dây cung : Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn , một cạnh là tia tiếp tuyến , một cạnh chứa một dây cung của đường tròn . chắn cung nhỏ AB , chắn cung lớn AB . 2/ Định lí : Số đo của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn . Chứng minh : Trường hợp tâm đường tròn nằm trên cạnh chứa dây cung . = 900 sđ = 1800 Suy ra : sđ Trường hợp tâm đường tròn năm bên ngoài góc Ta có : ( ABC vuông tại A ) Và : Suy ra : Mà : sđ= ( góc nội tiếp chắn cung AB ) Suy ra : sđ 3/ Hệ quả : Trong một đường tròn , góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau . Tiết 43 : LUYỆN TẬP I / Mục tiêu yêu cầu : Cho học sinh Rèn kĩ năng nhận biết góc tạo bởi tia tiếp tuyến và dây cung , áp dụng được định lí về số đo của góc tạo bởi tia tiếp tuyến và dây cung vào bài tập. Rèn tư duy lôgic và cách trình bày lời giải bài tập . II/ Chuẩn bị : Bảng phụ các đề bài tập và hình vẽ . III/ Tiến trình bài dạy : Hoạt động của giáo viên Nội dung Hoạt động 1 : Kiểm tra Phát biểu định lí , hệ quả của góc tạo bởi tia tiếp tuyến và dây cung . Hoạt động 2 : Sửa bài tập Bài tập 27 SGK trang 79 Bài tập 32 SGK trang 80 = sđ = sđ Hoạt động 3 : Luyện tập Bài tập 33 SGK trang 80 AB . AM = AC AN S ABC ANM ( Chung ) Bài tập 34 SGK trang 80 MT2 = MA . MB S MTB MAT ( chung ) áp dụng làm bài tập 35 Hoạt động 4 : Hướng dẫn về nhà Làm các bài tập còn lại , xem trước bài học sau . Bài tập 27 SGK trang 79 Ta có : ( Vì OA = OP ) Và (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung PB ) Suy ra : Bài tập 32 SGK trang 80 Ta có : = sđ (góc tạo bởi tia tiếp tuyến và dây cung và chắn cung PB ) Và = sđ ( Góc ở tâm chắn cung PB ) Suy ra : Mà : ( POT vuông tại P ) Suy ra : Bài tập 33 SGK trang 80 Ta có : (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AC ) Và ( so le trong ) Suy ra : S Mà : ( Chung ) Nên : ABC ANM Suy ra : Hay : AB . AM = AC AN Bài tập 34 SGK trang 80 Ta có : ( chung ) S Và (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung TA ) Nên : MTB MAT Suy ra : Hay : MT2 = MA . MB Tiết 44 : GÓC CÓ ĐỈNH Ở BÊN TRONG ĐƯỜNG TRÒN GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN I / Mục tiêu yêu cầu : Cho học sinh Nhận biết góc có đỉnh ở bên trong hay bên ngoài đường tròn . Phát biểu và chứng minh được định lí về số đo góc có đỉnh ở bên trong hay bên ngoài đường tròn Rèn luyện kĩ năng chứng minh chặt chẽ , rõ , gọn . . II/ Chuẩn bị : Bảng phụ có các hình vẽ . III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Kiểm tra Cho hình vẽ ... đa giác là gì ? Nêu ? Vẽ đường tròn tâm O bán kính 2 cm Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn O Vì sao tâm O cách đều các cạnh của lục giác đều ? gọi khoảng cách này là r Vẽ đường tròn ( O ; r ) Hoạt động 2 : Định lí Qua ? nhận xét và đưa đến định lí , đặc điểm của tâm hai đường tròn . Hoạt động 3 : Củng cố Làm bài tập 61 , 62 , 63 SGK trang 91 Hoạt động 4 : Hướng dẫn về nhà Làm bài tập 64 SGK trang 92 Học thuộc định nghĩa , định lí . Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác . Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác . Vì các dây bằng nhau . 1/ Định nghĩa : Đường tròn ngoại tiếp đa giác là đường tròn đi qua tất cả các đỉnh của đa giác và đa giác được gọi là đa giác nội tiếp đường tròn . Đường tròn nội tiếp đa giác là đường tròn tiếp xúc với tất cả các cạnh của đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn . 2/ Định lí : Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp , có một và chỉ một đường tròn nội tiếp . + Trong đa giác đều , tâm của đường tròn ngoại tiếp trùng với tâm đường tròn nội tiếp và được gọi là tâm của đa giác đều . Tiết 51: ĐỘ DÀI ĐƯỜNG TRÒN - CUNG TRÒN I / Mục tiêu yêu cầu : Cho học sinh Nhớ công thức tính độ dài đường tròn , biết cách tính độ dài cung tròn , vận dụng các công thức để tính các đại lượng chưa biết trong công thức và giải một vài bài toán thực tế . II/ Chuẩn bị : Bảng phụ ghi các bảng ở trang 93 , 94 . III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Kiểm tra và sửa bài tập 1/ Định nghĩa đường tròn ngoại tiếp đa giác , đường tròn nội tiếp đa giác . 2/ Sửa bài tập 64 SGK trang 92 Hoạt động 2 : Công thức tính độ dài đường tròn Nêu công thức tính chu vi đường tròn đã học . 3,14 là số gần đúng của số vô tỉ Pi ( kí hiệu ) Vậy công thức tính độ dài đường tròn bán kính R như thế nào ? Gọi d là đường kính thì công thức tính như thế nào ? Cho học sinh kiểm tra lại số qua thực hành như ? 1 Hoạt động 3 : Công thức tính độ dài cung tròn . Nêu ? 2 Hãy điền biểu thức thích hợp vào các chỗ trống ( ... ) trong dãy lập luận sau : Đường tròn bán kính R ( ứng với cung 3600 ) có độ dài là ... Vậy cung 10 , bán kính R có độ dài là = ... Suy ra cung n0 , bán kính R có độ dài là ... Hoạt động 4 : Bài tập 65 trang 94 SGK Bài tập 67 SGK trang 95 Hoạt động 5 : Hướng dẫn về nhà Học thuộc các công thức , làm các bài tập 68 , 70 , 73 , 74 SGK trang 95 , 96 Chu vi đường tròn bằng đường kính nhân với 3 , 14 C = 2R C = d Đường tròn bán kính R ( ứng với cung 3600 ) có độ dài là 2R Vậy cung 10 , bán kính R có độ dài là = Suy ra cung n0 , bán kính R có độ dài là R 10 5 1,5 3,18 4 d 20 10 3 6,37 8 C 62,8 31,4 9,42 20 25,12 R 10 40,8 21 n0 900 500 56,80 l 15,7 35,6 20,8 1/ Công thức tính độ dài đường tròn Độ dài C của một đường tròn bán kính R là : C = 2R Gọi d là đường kính thì : C = d ( đọc là Pi ) là một số vô tie , giá trị gần đúng là 3 , 14 2/ Công thức tính độ dài cung tròn . Trên đường tròn bán kính R , độ dài l của một cung n0 được tính theo công thức : l = Tiết 52: LUYỆN TẬP I / Mục tiêu yêu cầu : Cho học sinh Rèn luyện kĩ năng áp dụng công thức tính độ dài đường tròn , độ dài cung tròn , và các công thức suy luận của nó . Nhận xét và rút ra được cách vẽ một số đường cong chắp nối . Biết cách tính độ dài đường cong đó . Giải được một số bài toán thực tế . II/ Chuẩn bị : Bảng phụ vẽ hình 52 , 53 , 54 . III/ Tiến trình bài dạy : Hoạt động của giáo viên Nội dung Hoạt động 1 : Kiểm tra và sửa bài tập 1/ Nêu công thức tính độ dài đường tròn , độ dài cung tròn . 2/ Sửa bài tập 74 SGK trang 96 C = 40 000 km n0 = 200 01/ = 2000166 l ? Hoạt động 2 : Luyện tập Bài tập 71 SGK trang 96 Bài tập 72 SGK trang 96 C = 540 mm = 200 mm ? Bài tập 75 SGK trang 96 Chứng minh : Hoạt động 3 : Hướng dẫn về nhà Làm các bài tập còn lại , ôn lại công thức tính diện tích hình tròn đã học ở lớp dưới . Độ dài cung kinh tuyến từ Hà Nội đến xích đạo là : ( Km ) Bài tập 71 SGK trang 96 : Cách vẽ : Vẽ hình vuông ABCD cạnh 1 cm Vẽ cung AE tâm B bán kính BA = 1 cm , n0 = 900 Vẽ cung EF tâm C bán kính CE = 2 cm , n0 = 900 Vẽ cung FG tâm D bán kính DF = 3 cm , n0 = 900 Vẽ cung GH tâm A bán kính AG = 4 cm , n0 = 900 Bài tập 72 SGK trang 96 Ta có : = 1330 Vậy : = n0 = 1330 Bài tập 75 SGK trang 96 Ta có : = 2n0 ( Góc nội tiếp và góc ở tâm cùng chắn một cung ) Và : O’M = Nên : Vậy : Tiết 53: DIỆN TÍCH HÌNH TRÒN – HÌNH QUẠT TRÒN I / Mục tiêu yêu cầu : Cho học sinh Nhớ công thức tính diện tích hình tròn , biết cách tính diện tích hình quạt tròn Có kĩ năng vận dụng công thức vào giải toán . II/ Chuẩn bị : Bảng phụ ghi câu hỏi , hình vẽ , bài tập . III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Công thức tính diện tích hình tròn . Hãy nêu công thức tính diện tích hình tròn đã biết 3,14 là giá trị gần đúng của số Vậy diện tích S của hình tròn bán kính R được tính theo công thức nào ? Hãy điền kết quả vào các ô trống sau : R 3 10 S 15,26 78,5 Bài tập 77 trang 98 SGK Tính diện tích hình tròn nội tiếp một hình vuông có cạnh là 4 cm ( làm theo nhóm ) Hoạt động 2 : Cách tính diện tích hình quạt tròn Vẽ hình vẽ Hình có gạch sọc được gọi là hình quạt tròn OAB , tâm O , bán kính R , cung n0 , vậy hình quạt tròn là gì ? Treo bảng phụ có ? Hãy điền biểu thức thích hợp vào các chỗ trống ( ... ) trong dãy lập luận sau : Hình tròn bán kính R ( ứng với cung 3600 ) có diện tích là ... Vậy hình quạt tròn bán kính R , cung 10 có diện tích là ... Hình quạt tròn bán kính R , cung n0 có diện tích là ... Gọi điện tích hình quạt tròn là S . Hãy nêu công thức tính diện tích hình quạt tròn , bán kính R , cung n0 . Nêu công thức tính độ dài cung tròn , bán kính R , cung n0 Biến đổi và biểu thị tính S qua l Bài tập 79 SGK trang 98 Hoạt động 3 : Luyện tập Làm theo nhóm bài tập 81 SGK trang 99 ( 3 nhóm 3 câu ) Bài tập 82 SGK trang 99 Hoạt động 4 : Dăn dò về nhà Học thuộc các công thức . làmg các bài tập 78 , 83 SGK trang 98 , 99 Bình phương bán kính nhân 3 , 14 S = R2 R 3 10 2 5 S 28,26 314 15,26 78,5 Ta có d = AB = 4 cm Suy ra R = 2 cm Diện tích hình tròn đó là : S = R2 3,14. 22 15,26 cm2 Hình quạt tròn là hình tạo bởi một cung tròn và hai bán kính đi qua hai mút của cung đó . Hình tròn bán kính R ( ứng với cung 3600 ) có diện tích là R2 Vậy hình quạt tròn bán kính R , cung 10 có diện tích là Hình quạt tròn bán kính R , cung n0 có diện tích là S = L = S = = . = R C S N0 Sq 2,1 13,2 13,8 47,50 1,83 2,5 15,7 19,6 229,60 12,5 3,5 22 37,8 1010 10.6 1/ Công thức tính diện tích hình tròn . Diện tích S của hình tròn bán kính R được tính theo công thức : S = R2 2/ Cách tính diện tích hình quạt tròn : a)Khái niệm hình quạt tròn : Hình quạt tròn là hình tạo bởi một cung tròn và hai bán kính đi qua hai mút của cung đó . Hình quạt tròn OAB , tâm O , bán kính R , cung n0 b) Công thức tính diện tích hình quạt tròn Diện tích hình quạt tròn bán kính R cung n0 được tính theo công thức : S = Hoặc : S = Tiết 54: LUYỆN TẬP I / Mục tiêu yêu cầu : Cho học sinh Củng cố kĩ năng vẽ hình ( các đường cong chắp nối ) , kĩ năng vận dụng công thức tính diện tích hình tròn , diện tích hình quạt tròn vào giải toán . Được giới thiệu diện tích hình viên phấn , hình vành khăn và cách tính diện tích các hình đó . II/ Chuẩn bị : Bảng phụ ghi câu hỏi , hình vẽ , bài tập . III/ Tiến trình bài dạy : Hoạt động của giáo viên Hoạt động của học sinh Nội dung Hoạt động 1 : Kiểm tra và Sửa bài tập 1/ Nêu công thức tính diện tích hình tròn . 2/ Nêu công thức tính hình quạt tròn . Diện tích hình quạt tròn , bán kính R , cung 1800 là ? 3 / Sửa bài tập 78 SGK trang 98 Hoạt động 2 : Luyện tập Bài tập 83 SGK trang 99 Treo bảng phụ có hình vẽ Nêu cách vế Đặt tên cho diên tích các nửa đường tròn là S1 , S2 , ... Nêu cách tính diên tích hình HOABINH Tính cụ thể Tính diện tích đường tròn đường kính NA Bài tập 85 SGK trang 100 Treo hình vẽ Hình gạch sọc được gọi là hình viên phấn AmB . Vậy hình viên phấn là gì ? Để tính diện tích hình viên phấn ta làm thế nào ? Tính cụ thể Bài tập 86 SGK trang 100 Treo hình vẽ Phần gạch sọc được gọi là hình vành khăn Vậy hình vành khăn là gì ? Để tính diện tích hình vành khăn ta làm gì ? Cho làm theo nhóm , mỗi nhóm làm mỗi câu . Làm bài 87 SGK trang 100 ( Nếu còn thời gian ) Hoạt động 3 : Hướng dẫn về nhà Tiết sau ôn tập chương III Học thuộc các định nghĩa , định lí phần : Tóm tắc các kiến thức cần nhớ “ Làm các bài tập 88 , 89 , 90 ,91 SGK trang 103 , 104 . Diện tích hình HOABINH bằng tổng nửa đường tròn ( M ) với nửa đường tròn Đường kính OB trừ diện tích hai nửa đường tròn đường kính HO Hình viên phấn là phần hình tròn giới hạn bởi một cung và dây căng cung ấy . Lấy diện tích hình Quạt OAB trừ đi diện tích tam giác OAB . Hình vành khăn là phần hình tròn nằm giữa hai đường tròn đồng tâm Diện tích đường tròn lớn trừ diện tích đường tròn nhỏ . Kết quả : S = Bài tập 83 SGK trang 99 Cách vẽ : Vẽ nửa đường tròn tâm M đường kính HI = 10 cm Trên HI lấy O và B sao cho HO = BI = 2 cm Vẽ hai nửa đường tròn đường kính HO và BI cùng phía với Nửa đường tròn đường kính HI . Vẽ nửa đường tròn đường kính OB khác phía với nửa đường tròn đường kính HI . Vẽ đường thẳng vuông góc với HI tại M và cắt nửa đường tròn đường kính HI tại N , cắt nửa đường tròn đường kính OB tại A . b)Ta có : OB = HI –2HO = 10 – 2.2 = 6 ( cm ) Diện tích nửa đường tròn đường kính OB là : S1 = ( cm2 ) Diện tích nửa đường tròn đường kính HI là : S2 = ( cm2 ) Diện tích hai nửa đường tròn đường kính HO là : S3 = ( cm2 ) Diện tích hình HOABINH là : S = S1 + S2 –S3 = ( cm2 ) c)Ta có NA = NM + MA = 5 + 3 = 8 Diện tích đường tròn đường kính NA là S4 = ( cm2 ) Vậy S = S4 Bài tập 85 SGK trang 100 Diện tích hình quạt tròn OAB là : Sq = Vẽ AH vuông góc với OB ta có : AH = OA .sin 600 = 5. Diện tích tam giác OAB là : SOAB = ( cm2 ) Diện tích hình viên phấn AmB là : 13 , 61 –11,23 = 2 , 38 ( cm2 ) Bài tập 86 SGK trang 100 a)Diện tích hình tròn ( O ; R1 ) là : S1 = R12 Diện tích hình tròn ( O ; R2 ) là : S2 = R22 Diện tích hình vành khăn là : S = S1 –S2 = R12 - R22 = (R12 –R22 ) Diện tích hình tròn ( O ; 10,5 ) là : S1 = 10,52 Diện tích hình tròn ( O ; 7,8 ) là : S2 = 7,82 Diện tích hình vành khăn là : S = S1 –S2 = 10,52 -7,82 = (10,52 –7,82 ) = 155,1 ( cm 2 )
Tài liệu đính kèm:
 HH 9 CHUONG 3.doc
HH 9 CHUONG 3.doc





