Giáo án Hình học 8 - Tiết 68: Ôn tập chương IV - Năm học 2009-2010 - Phạm Xuân Diệu

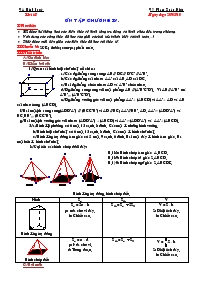
 TiÕt 68 Ngµy d¹y: 20/05/10
 ÔN TẬP CHƯƠNG IV.
I/ Mục tiêu:
HS được hệ thống hoá các kiến thức về hình lăng trụ đứng và hình chóp đều trong chương.
Vận dụng các công thức đã học vào giải các bài tập (nhận biết và tính toán,)
Thấy được mối liên giữa các kiến thức đã học với thực tế.
II/ Chuẩn bị: SGK; thước; com-pa; phấn màu.
III/ Tiến trình:
	A/ Ổn định lớp:
	B/ Kiểm bài cũ:
	1/ Quan sát hình hộp chữ nhật rồi chỉ ra:
 a/ Các đg/thẳng song song: AB // DC // D’C’ // A’B’.
 b/ Các đg/thẳng cắt nhau: AA’ cắt AB, AD cắt DC.
 c/ Hai đg/thẳng chéo nhau: AD và A’B’ chéo nhau.
 d/ Đg/thẳng song song với mặt phẳng: AB // (A’B’C’D’). Vì AB // A’B’ mà A’B’Ì (A’B’C’D’).
 e/ Đg/thẳng vuông góc với mặt phẳng: AA’^ (ABCD) vì AA’^ AD và AB cắt nhau trong (ABCD).
 f/ Hai mặt/ph song song (ADD’A’) // (BCC’B’) vì AD // BC; AA’// BB’, AD, AA’Ì (ADD’A’) và BC, BB’Ì (BCC’B’).
 g/ Hai mặt/ph vuông góc với nhau: (ADD’A’) ^ (ABCD) vì AA’Ì (ADD’A’) và AA’^ (ABCD).
	2/ a/Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh. Các mặt là những hình vuông. 
	 b/ Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh. Các mặt là hình chữ nhật.
	 c/ Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh. Hai mặt đáy là hình tam giác. Ba mặt bên là hình chữ nhật. 
	 3/ Gọi tên các hình chóp dưới đây:
H.138: Hình chóp tam giác A.BCD.
H.139: Hình chóp tứ giác S.ABCD.
H.140: Hình chóp ngũ giác S.ABCDE.
Hình lăng trụ đứng, hình chóp đều.
Hình
Sxq
Stp
V
Hình lăng trụ đứng
Sxq = 2p . h.
p: nửa chu vi đáy.
h: Chiều cao.
Stp = Sxq + 2Sđ.
V = S . h.
S: Diện tích đáy.
h: Chiều cao.
Hình chóp đều
Sxq = p . d.
p: Nửa chu vi.
d: Trung đoạn.
Stp = Sxq + Sđ.
V =.S . h.
S: Diện tích đáy.
h: Chiều cao.
	C/ Bài mới:
Hoạt động của thầy,trò
Hoạt động của trò
Tính diện tích xung quanh, toàn phần và th/tích của h/lăng trụ đáy là h/vuông như thế nào?
Vì có 4 hình chữ nhật kích thước như nhau nên Sxq = 4ah.
 Stp = Sxq + 2Sđ.
 V = Sđ . h = a2.h.
Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ đứng tam giác đều như thế nào?
Các mặt bên là 3 hình chữ nhật kích thước như nhau nên:
 Sxq = 3ah.
 Stp = 3ah + 2.
 V =.h.
Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ lục giác đều là bao nhiêu?
Sxq = 5ah.
 Stp = 5ah + 2.
 V =.h.
Muốn tính diện tích xung quanh hình lăng trụ đáy là hình thoi ta làm thế nào? Stp ; V bằng bao nhiêu?
Sxq = 4.5a.h.
 Stp = 20ah + 2.24a2.
 V = 24a2.h.
Muốn tính số bê tông ta phải tính như thế nào?
Cần tính ra thể tích h/lăng trụ đáy là ngũ giác ABCFE.
 Số chuyến: 0,5964:0,06 » 10
Muốn tính diện tích đáy của hình lăng trụ đáy là h/th cân ta làm như thế nào?
Vì là h/th cân nên:
AH==
 == 3,16. 
Trong h/hộp chữ nhật với 3 kích thước a, b, c thì độ dài đg/chéo AD được tính theo công thức nào?
AD =. Và tương tự cho các cạnh còn lại.
Thể tích h/chóp cụt đều phải tính như thế nào?
Ta dựa vào:
 Vh/ch = VL.ABCD – VL.EFGH .
Mà
VL.EFGH =.102.15 = 500cm3.
VL.ABCD =.202.30 = 4000cm3.
Vh/ch = 4000 – 500 = 3500cm3.
51/127 Tính diện tích xung quanh, diện tích toàn phần và thể tích đứng có chiều cao h và đáy là:
a/ Hình vuông cạnh a.
 Sxq = 4ah.
 Stp = 4ah + 2a2.
 = 2a(2h + a).
 V = a2.h.
b/ Tam giác đều cạnh a.
 Sxq = 3ah.
 Stp = 3ah + 2 = 3ah += a(3h +)
 V =.h.
 c/ Lục giác đều cạnh a.
 Sxq = 6ah.
 Sđ = 6 =. Stp = 6ah + .2.
 V =.h.
 d/ Hình thang cân, đáy lớn 2a, các cạnh còn lại là a.
 Sxq = 5ah.
 Sđ =.
 Stp = 5ah + 2= a(5h + ).
 V =.h.
 e/ Hình thoi có 2 đg/chéo là 6a và 8a.
 Cạnh h/thoi đáy là: AB == 5a.
 Sxq = 4.5a.h = 20ah.
 Sđ = = 24a2.
 Stp = 20ah + 2.24a2 = 20ah + 48a2 = 4a(5h + 12a)
 V = 24a2.h.
54/128
 Ta tính được: SABCD = 21,42m2; SDEF = 1,54m2.
 SABCFE = 19,88m2.
 a/ Lượng bê tông là: V = 19,88 . 0,03 = 0,5964m3.
 b/ Vì số chuyến là số nguyên nên có 10 chuyến.
52/128
 Diện tích xung quanh khối gỗ là:
 Sxq = 3.11,5 + 6.11,5 + 2.3,5.11.5 =
 = 184cm2.
 Độ dài đg/cao hình thang cân đáy là:
 AH === 3,16
Và dễ c/m AD = HK = 3; CK = BH = 1,5.
Diện tích đáy là:
 Sđ == 14,22cm2.
 Vậy diện tích toàn phần của khối gỗ là: 
 Stp = Sxq + 2Sđ = 184 + 2.14,22 = 212,44cm2.
55/128 Quan sát hình rồi điền số thích hợp vào ô trống:
AB
BC
CD
AD
1
2
2
3
2
3
6
7
2
6
9
11
9
12
20
25
57/129 
Tính thể tích của hình chóp đều sau:
 Diện tích đáy của h/chóp là:
 Sđ === 25cm2.
 Thể tích h/chóp là:
 V =.25.20 » 288,33cm3.
 Tính thể tích của hình chóp cụt đều:
Ta biết Vh/ch = VL.ABCD – VL.EFGH .
 VL.EFGH =.102.15 = 500cm3.
 VL.ABCD =.202.30 = 4000cm3.
Vậy thể tích của hình chóp cụt là: 
 Vh/ch = VL.ABCD – VL.EFGH = 4000 – 500 = 3500cm3.
	D/ Củng cố theo từng phần:
IV/ Hướng dẫn ở nhà:
Tự ôn lại nắm vững vị trí tương đối giữa đg/thẳng và đg/thẳng (song song, cắt nhau, chéo nhau); giữa đg/th và mặt/ph; giữa 2 mặt/ph (song song, vuông góc).
Nắm vững khái niệm hình hộp chữ nhật, hình lập phương, hình lăng trụ đứng, lăng trụ đều, hình chóp đều.