Giáo án bổ trợ Hình học Lớp 8 học kì II - Năm học 2007-2008 - Vũ Văn Hòa
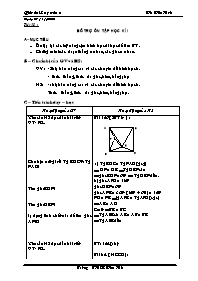
a/ Tg EDC = Tg FAD (gcg)
DF = DE Tg DEF cân
góc EDF = 600 Tg DEF đều.
b/ góc AFD = 1800
góc DEF = 600
góc AFE = 3600-(1500 + 600) = 1500
FD = FE tgAFE = TgAFD (cgc)
AE = AD
Cmtt BE = BC
TgABE có AE = AB = BE
TgABE đều
Bạn đang xem 20 trang mẫu của tài liệu "Giáo án bổ trợ Hình học Lớp 8 học kì II - Năm học 2007-2008 - Vũ Văn Hòa", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày 07 / 1/ /2008 Tiết 38 : bổ trợ ôn tập học kì i A – Mục tiêu Ôn tập lại các kỹ năng c/m hình học đã học để làm BT . Chứng minh các đoạn thẳng = nhau, các góc = nhau. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT - KL Có nhận xét gì về Tg EDC & Tg FAD? Tìm góc EDF? Tìm góc DEF? áp dụng tính chất nào để tìm góc AFE? Bài 156 ( SBT tr ) : F E A B C D a/ Tg EDC = Tg FAD (gcg) DF = DE Tg DEF cân góc EDF = 600 Tg DEF đều. b/ góc AFD = 1800 góc DEF = 600 góc AFE = 3600-(1500 + 600) = 1500 FD = FE tgAFE = TgAFD (cgc) AE = AD Cmtt BE = BC TgABE có AE = AB = BE TgABE đều Yêu cầu HS đọc đầu bài viết GT - KL C/m Tg ABMD là hv làm thế nào? Sử dụng dấu hiệu nào để c/m tg BDC vuông cân ở B? Q đóng vai trò gì trong Tg ADP? Vì sao? BT: 154 (sbt) Bài 84 ( NCCĐ ) : A B D M C M Q P a/ Tg ABMD có 4 cạnh = nhau ; Â = 900 ABMD là hv Tg BCD có MB = MD = MC ; góc BDC = 450 tg BDC vuông cân ở B b/ PQ//DM & PQ = DM DMPQ là hbh c/ Q là trực tâm của Tg ADP AQ vuông góc DP D- BTVN: ; 142,146,148,(SBT) Ngày 12 /1 /2008 Tiết 40 : bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT - KL Ta có các tam giác nào có diện tích bằng nhau ? Vì sao? a. Tính tỉ số diện tích của tam giác DAC và tam giác DCK? b. Tính tỉ số diện tích của tam giác DAC và tứ giác ADLB? c. Tính tỉ số lượng giác của các tứ giác ABKD và ABLD ? Yêu cầu HS đọc đầu bài viết GT – KL Bài 55 ( SBT tr 132 ) : Ta có: SACD= SBCD= SDAB= SCAB= SABCD. Và SDBK=SDKL=SDLC= SDBC SABK =SAKL=SALC= SABC Do đó: SDBK=SDKL=SDLC= SABK =SAKL=SALC a. b. c. Bài 54 ( SBT tr132 ) : - Hãy so sánh diện tích của tam giác AMN và tam giác ABC? - So sánh diện tích của tam giác AMB với diện tích cảu tam giác ABC? - Em nhận xét gì về hai đường chéo của đa giác ABMN ? (vuông góc với nhau) - Em hãy tính diện tích của đa giác ABMN ? - Tính diện tích của tam giác ABC theo AM và BN ? Ta có: SAMN=SAMB=SABC SAMB= SABC Diện tích của đa giác ABMN là: SABMN= AM.BN Mặt khác, diện tích của đa giác còn được xác định bởi: SABMN= SAMN + SAMB = SABC Do đó ta có: AM.BN = SABC Suy ra: SABC = AM.BN. Yêu cầu HS đọc đầu bài viết GT - KL - Em hãy tìm các hình có diện tích bằng nhau ? - Diện tích của đa giác ABEFO và đa giác ADFEO bằng tổng diện tích của các đa giác nào ? Bài 102( NCCĐ ) : DABC = DADC ị SABC=SADC DOEC = DOFC ị SOEC= SOFC Mà SABEO = SABC - SOEC SADFO = SADC - SOFC Suy ra: SABEO = SADFO.(1) Mặt khác: SABEFO = SABEO + SOEF (2) SADFEO= SADFO + SOEF (3) Từ (1), (2), (3) ta có: SABEFO = SADFEO D- BTVN: BT104 (NCCĐ) ; 53, 54, 56(SBT) Tuần21: định lí talét trong tam giác A – Mục tiêu Rèn kỹ năng chứng minh vận dụng định lí Talét, định lí đảo và hệ quả . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT - KL - Áp dụng định lí Talét trong tam giác ABC em có các đoạn thẳng tương ứng tỉ lệ nào ? - HS nêu 3 cặp đoạn thẳng tương ứng tỉ lệ. - GV nhấn mạnh: ta nên chọn cặp đoạn thẳng nào để tiện cho việc tính toán. - Hình 2 học sinh làm tương tự. Bài 3 ( SBT tr65 ) : - Hình 1: Trong tam giác ABC có MN // BC, M ẻ AB, M ẻ AC nên ta có: Hay Suy ra x = = 15,3 - Hình 2: Trong tam giác PQR có EF // QR, ẺPQ, E ẻ PR nên ta có: Hay ị x = 28. Yêu cầu HS đọc đầu bài viết GT – KL - GV hướng dẫn học sinh: kéo dài các tia DA, CB cắt nhau tịa E, áp dụng định lí Talet trong các tam giác ECD và EMN. - Sau đó áp dụng tính chất của tỉ lệ thức để có ĐPCM. - áp dụng tính chất của tỉ lệ thức em suy ra được dãy tỉ số nào ? - Phần c học sinh làm tương tự. Bài 4 ( SBT tr 66 ) : a. áp dụng định lí Talét vào tam giác ECD có AB // CD nên: ị (1) Tương tự với tam giác EMN có AB // MN nên: ị (2) Từ (1) và (2) ta có: Hay b. Theo chứng minh trên có: ị ị c. Từ phần b có: ị Nên: Hay . Yêu cầu HS đọc đầu bài viết t(giây) GT - KL - Muốn chứng minh AE2 = EK.EG ta cần chứng minh gì? í í ; - HS lên bảng trình bày lời giải. - Muốn c/m í í ; Bài 142 ( NCCĐ ) : a)áp dụng hệ quả của đl Talet trong DABE với AB // DG ta có: (1) Tương tự với D BEK với AD // BK nên: (2) Từ (1, (2) có: ị AE2 = EK.EG. b. Từ (1) ta có: Hay (3) Từ (2) có: (4) Cộng hai vế của (3) và (4) có: Hay D- BTVN: BT141 (NCCĐ) ;7, 8, 9 (SBT) Tuần 23: củng cố về tính chất đường phân giac trong tam giác A – Mục tiêu Rèn kỹ năng chứng minh vận dụng tính chất đường phân giác trong tam giác. Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - Hãy tính tỉ số của BD và DC, EC và EA, FA và FB theo các cạnh của tam giác ABC ? Yêu cầu HS đọc đầu bài viết GT – KL - Enm hãy tính độ dài cạnh BC? - Tỉ số của BD và DC là bao nhiêu? - Tính DE như thế nào ? - Muốn tính được diện tích của hai tam giác em cần phải tính được yếu tố nào? (đường cao AH). - GV gợi ý HS tính theo cách 2: dựa vào tie số của hai tam giác có cùng chiều cao. Bài 18( SBT tr69 ) : Ta có: ; ; Nhân các vế của các tỉ lệ thức trên ta được: = = 1 Bài 21 ( SBT tr70 ) : a. áp dụng định lí Pitago trong DABC có: BC= 35 cm. Theo tính chất đường phân giác trong tam giác ABC có: . Mà BD + CD= BD = 35. Nên: BD = 35:7.3= 15 cm; CD = 20cm. - áp dụng định lí Talét trong tam giácABC với DE // AB có: ị DE = 12 cm. b. Ta có đường cao AH là: AH = Do đó: SABD= 126cm2 SACD= =168 cm2 Yêu cầu HS đọc đầu bài viết GT – KL - Muốn c/m DE // BC ta cần chứng minh gì ? í í ; ; BM = MC - GV hướng dẫn học sinh có thể áp dụng tính chất về đường trung bình trong tam giác để c/m bài này. Bài 151 ( SNC tr 43 ) : a. Xét DABM có DM là p/g của góc AMB nên: (t/c) Tương tự có: Mà BM = CM. Do đó ta có: . Theo định lí Talét đảo suy ra DE // BC. b.Theo ĐL ta lét có: ị DI = IE D- BTVN: BT 152(NCCĐ) ; 19, 20, 22(SBT) Tuần 25: các trường hợp đồng dạng của tam giác A – Mục tiêu Rèn kỹ năng chứng minh vận dụng khái niệm và tính chất của tam giác đồng dạng Rèn kỹ năng vẽ hình chính xác và vận dụng vào thực tế . B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - Biết DABC ∽DA’B’C’ ta suy ra các cạnh nào tương ứng tỉ lệ với nhau ? - Cạnh nào của ∽DA’B’C’ là nhỏ nhất, lớn nhất ? - Tính các cạnh ảu ∽DA’B’C’ ? Bài 27 ( SBT tr 71 ) : a. Ta có: A’B’ = 16,2 + 10,8 = 27 cm; Và Nên: . Suy ra: A’C’= 54,5 cm; B’C’ = 40,5 cm b. Tương tự phần a ta có:A’B’ = 10,8 cm; B’C’ = 16,2 cm; C’A’ = 21,8 cm. Yêu cầu HS đọc đầu bài viết GT – KL - Taị sao tam giác ADE và tam giác ABE đồng dạng với nhau? - Lưu ý học sinh viết đúng đỉnh tương ứng của hai tam giác đồng dạng. Bài 28 ( SBT tr 71 ) : - Xét DABE và DABE có: Cạnh AE chung góc BAE = góc DAE (slt) AB = DE (gt) ị DABE = DEDA ị DABE∽ DEDA - C/m tương tự ta có: DABE∽ DCEB - Theo tính chất bắc cầu suy ra DEDA∽ DCEB. Do đó: DABE∽ DEDA ∽ DCEB Yêu cầu HS đọc đầu bài viết GT – KL - Giả sử DABC ∽DA’B’C’ thì tỉ số chu vi của hai tam giác bằng bao nhiêu ? (bằng tỉ số đồng dạng) - Vậy suy ra tỉ số dd là bao nhiêu? - GV nhấn mạnh : Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng? Bài 159( SNC tr 47 ) : Giả sử DABC ∽DA’B’C’. Khi đó ta có: Mặt khác DABC ∽DA’B’C’ suy ra: Mà A’B’ – AB = 1. Do đó: ị Hay ị AB = 5,5 cm Và A’B’ = 6,5 cm. D- BTVN: BT160 (NCCĐ) ; 25, 26(SBT) Tuần 27: bài tập về các th đồng dạng của tam giác A – Mục tiêu Rèn kỹ năng chứng minh vận dụng các trường hợp đồng dạng của 2 tam giác đồng dạng . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - Muốn chứng minh DPQR ∽DABC ta cần c/m gì? í - HS lên bảng c/m. - Yêu cầu học sinh tìm tỉ số đồng dạng cuả hai tam giác. Bài 31( SBT tr 72 ) : Xét DOAB có PQ là đtb của tam giác nên: AB =2PQ ị 2. Tượng tự ta có = 2 ; = 2. Do đó: Khi đó DPQR ∽DABC(c.cc) Yêu cầu HS đọc đầu bài viết GT – KL - Nêu các bước của bài toán dựng hình ? - Phát biểu định lí về hai tam giác đồng dạng ? - Dựa vào đó để nêu cách dựng - HS chứng minh cho cách dựng trên của mình. - GV hướng dẫn học sinh dựng dựa vào bài 31 (SBT) Bài 34 ( SBT tr 72 ) : - Dựng các điểm D và E theo thứ tự trên cạnh AB và AC sao cho: ; - Dựng đoạn thẳng DE. Khi đó DADE ∽DABC theo tỉ số đồng dạng . Yêu cầu HS đọc đầu bài viết GT – KL - Giả sử cho trước DABC có chu vi là 2p. Dựng DAB’C’ có chu vi là 2p’ và đồng dạng với DABC. - Tỉ số đồng dạng của hai tam giác là bao nhiêu ? - HS nêu cách dựng. - Hs nêu cách chứng minh. Bài 160 ( SNC tr47 ) : * Cách dựng: - Trên tia AB lấy điểm B’ sao cho: . - Qua B’ dựng đường thẳng song song với BC cắt tia AC ở C’. - Tam giác AB’C’ là tam giác cần dựng. * CHứng minh: Theo cách dựng ta có: B’C’ // BC nên DABC ∽DAB’C’. Do đó: = Mà Ab + BC + AC = 2p . Suy ra: AB’ + B’C’ + AC’ = 2p’. Vậy DAB’C’ thoả mãn yêu cầu của đề bài. D- BTVN: BT161 (NCCĐ) ; 33, 34(SBT) Ngày 29 / 1/2008 Tiết 50: bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh vận dụng các trường hợp đồng dạng của 2 tam giác đồng dạng . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - Muốn c/m góc BAD bằng góc DBC em sẽ c/m 2 tam giác dd nào? í DABD ∽DBDC í ; góc ABD = góc BDC Bài 36 ( SBT tr 72 ) : a. Xét DABD và DBDC có: = ; góc ABD = góc BDC Suy ra: DABD ∽DBDC (c.g.c) Do đó: góc BAD = góc DBC. b. Mặt khác: DABD ∽DBDC ị Suy ra: BC = 2AD. Yêu cầu HS đọc đầu bài viết GT – KL - GV cho thêm phần a: - Em hãy c/m DDBA ∽DABC. - Tỉ số bằng tỉ số nào? (=) - Tỉ số bằng tỉ số nào? (=) - Tỉ số bằng tỉ số nào? (=) Bài 42 ( SBT tr 74 ) : a. Xét DDBA và DABC có: Góc B chung. ADB = BAC = 900 ị DDBA ∽DABC (g.g) b. Xét DABC có BE là tia p/g của góc ABC nên: = (t/c) (1) Mà DDBA ∽DABC ị = (2) Mặt khác trong DDBA có BF là tia p/g của góc ABD nên: = (t/c) (3) Từ (1), (2), (3) ta có: = Yêu cầu HS đọc đầu bài viết GT – KL - So sánh các tam giác ABC và ADE? - Từ đó có các cặp cạnh nào tương ứng tỉ lệ ? - Em nhận xét gì về hai tam giác FDB và FCE ? Bài 161 ( SNC tr 47 ) : a. Xét DABC và DADE có: ; góc A chung Suy ra DABC ∽ DADE (c.g.c) b. Do DABC ∽ DADE nên: . Hay ị DE = 1,8 cm. c. DFDB ∽ DFCE (g.) nên: ị Từ đó tính được FD = 2,1 cm. D- BTVN: BT 165(NCCĐ) ; 37, 38, 43 (SBT) Ngày 2/ 1/2008 Tiết 52: bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh vận dụng các trường hợp đồng dạng của 2 tam giác vuông. Rèn kỹ năng vẽ hình chính xác và vận dụng vào thực tế. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - Em có nhận xét gì về hai tam giác ABC và MDC ? - Hãy tính độ dài DC ? Bài 44 ( SBT tr 74 ) : Xét DABC và DMDC có: Góc A = góc M = 900; Góc C chung ị DABC ∽ DMDC (g.g) Do đó: . Hay ị DC = 32 cm. Yêu cầu HS đọc đầu bài viết GT – KL - Muốn c/m BD // AC ta cần c/m gì? í Góc DBC = góc ACB í DABC ∽ DCDB - Hs lên bảng c/m. Bài 46 ( SBT tr 75 ) : Xét DABC và DCDB có: Góc A = góc C = 900 ị DABC ∽ DCDB (ch. cgv) Suy ra Góc DBC = góc ACB (ĐN) Mặt khác hai góc trên là hai góc slt của AC và BD tạo bởi BC. Do đó BD // AC. Yêu cầu HS đọc đầu bài viết GT – KL - GV gợi ý: Qua A và C kẻ các đt // với BD, cắt MN lần lượt tại E và F. - Tam giác APE đồng dạng với tam giác nào? - Tam giác CQF đồng dạng với tam giác nào? - So sánh tỉ số và ? Bài 177 ( SNC tr 49 ) : Ta có: DAPE∽DDPM (g.g)ị DCQF∽DBQM (g.g)ị DANE∽DCNF(g.c.g) ị AE = FC. Mặt khác MD = BM (gt). Suy ra: = Do đó: . D- BTVN: BT 178(NCCĐ) ; 45, 47, 48 (SBT) Ngày 5 /2 /2008 Tiết 54: bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh vận dụng các trường hợp đồng dạng của 2 tam giác đồng dạng . Rèn kỹ năng vẽ hình chính xác và vận dụng vào thực tế. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - HS c/m AH2 = BH.CH. - Tính diện tích của tam giác ABC? - Tính diện tích của tam giác ABM? - Tính diện tích của tam giác AHM? Bài 50 ( SBT tr 75 ) : Xét DBAH và DAHC có: Góc AHB = Góc AHC = 900 Góc BAH = góc ACH (cùng phụ với góc HAC) ị DBAH ∽ DACH (g.g) Suy ra ị AH2 = CH. BH= 36 SABC= = 39cm2 SABM= SABC : 2 = 19,5cm2 SABH= = 12cm2 ị SAHM= SABM - SABH = 7,5cm2. Yêu cầu HS đọc đầu bài viết GT – KL - Em hãy c/ m DABO ∽DDCO ? - DBCO ∽ DADO theo trường hợp nào ? - HS lên bảng c/m. Bài 52 ( SBT tr 76 ) : a. Xét DABO và DDCO có: Góc BAO = góc ODC (gt). Góc AOB = góc COD (đối đỉnh) ị DABO ∽DDCO (g.g) b. Xét DBCO và DADO có: (DABO ∽DDCO) Góc BOC = góc AOD (đối đỉnh) ị DBCO ∽ DADO (c.g.c) Yêu cầu HS đọc đầu bài viết GT – KL - GV hướng dẫn HS : kẻ BD ^ AC tại D. - So sánh hai góc CBD và HAC ? - Nhận xét gì về hai tam giác DBC và EAH ? - Nhận xét gì về vị trí của điểm E đối với BC ? - GV nhắc lại: tỉ số của hai đường trung tuyến tương ứng của hai tam giác đồng dạng = tỉ số đồng dạng. Bài 191 ( SNC tr 53 ) : - Ta có: góc CBD = HAC ( phụ với góc C) - Khi đó DDBC ∽DEAH (g.g) suy ra: . - Điểm E là trung điểm của CD ị BE là đường trung tuyến của DDBC - Và AO là đường trung tuyến của DAHE. - Do đó: ị DCBE ∽DHAO (c.c.c) ị Góc CBE = Góc HAO. ị BE ^ AO. D- BTVN: BT 190 (NCCĐ) ; 51, 53, 54 (SBT) Ngày 9 /2 /2008 Tiết 56: bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh vận dụng định lí Talét, định lí đảo và hệ quả và các trường hợp đồng dạng của hai tam giác đồng dạng . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - C/m DAHB ∽DBCD ? - Từ đó suy ra các đoạn thẳng nào tương ứng tỉ lệ ? - tính AH ? - Muốn tính diện tích tam giác AHB em cần biết độ dài cạnh nào ? (BH) - Tỉ số diện tích của hai tam giác đồng dạng được tính như thê nào ? Bài 53( SBT tr 76 ) : a. Xét DAHB và DBCD có: Góc AHB = góc C = 900 Góc ABH = góc CDB (slt) ị DAHB ∽DBCD (g.g) b. Do DAHB ∽DBCD ta có: Hay ị AH = 7,2 cm. c.* Cách 1: SAHB = * Cách 2: SBCD = = = 54 cm2 Mà ị SAHB = = 43,2 Yêu cầu HS đọc đầu bài viết GT – KL - So sánh DAFH và DCDH ? - So sánh DBFH và DCEH ? Bài 55 ( SBT tr ) : Ta có DAFH ∽DCDH (g.g) ị ị AH.DH = CH. FH (1) Tương tự DBFH ∽DCEH (g.g) ị ị BH.EH = CH.FH (2) Từ (1) và (2) ta có: AH.DH = CH. FH = BH.EH. Yêu cầu HS đọc đầu bài viết GT – KL - Nhận xét gì về hai tam giác ACP và MKP ? - So sánh AC và MK ? - Nhận xét gì về vị trí tương dối của hai đường thẳng MK và AC ? Bài 56 ( SBT tr 77 ) : Xét DACP và DMKP có: Góc KPM = góc APC (đối đỉnh) ị DACP ∽DMKP (c.g.c) ị ị AC = 2.MK. (1) Mặt khác: DACP ∽DMKP ị Góc PAC= góc PKM. Và hai ở vị trí slt ị MK // AC (2) Từ (1) và (2) có MK là ĐTB của DABC Vậy AK và CM là hai đường trung tuyến của DABC. D- BTVN: BT 199 (NCCĐ) ; 54, 57(SBT) Ngày 13 /2 /2008 Tiết 58: bổ trợ ôn tập A – Mục tiêu Rèn kỹ năng chứng minh vận dụng định lí Talét, định lí đảo và hệ quả và các trường hợp đồng dạng của hai tam giác đồng dạng . Rèn kỹ năng vẽ hình chính xác. B – Chuẩn bị của GV và HS: GV: - Sbt, toán nâng cao và các chuyên đề hình học 8. - thước thẳng, thước đo góc, ê ke, bảng phụ HS : - sbt, toán nâng cao và các chuyên đề hình học 8. Thước thẳng, thước đo góc, ê ke, bảng phụ. C – Tiến trình dạy – học: Hoạt động của GV Hoạt động của HS Yêu cầu HS đọc đầu bài viết GT – KL - So sánh hai tam giác ADN và AMB ? - Em có nhận xét gì về hai tam giác MAN và ABC ? Bài ( SBT tr ) : Xét DADN và DAMB có: Góc AND = góc AMB = 900 Góc D = góc B ị DADN ∽DAMB (g.g) Suy ra: ị Xét DMAN và DABC có: ị Góc MAN = góc ABC (phụ với góc BAM) ị DMAN ∽DABC (c.g.c) Yêu cầu HS đọc đầu bài viết GT – KL - Em có nhận xét gì về DABG và DACE ? - Nhận xét gì về tam giác CBG và tam giác ACF ? - Cộng các vế của (1) và (2) em có điều gì ? Bài ( SBT tr ) : Ta có DABG ∽ DACE (g.g) ị AB.AE = AC.AG. (1) Tương tự có DCBG ∽ DACF (g.) ị BC.AF = AC.CG (2) Cộng hai vế của (1) và (2) ta có: AB.AG + BC.AF = AC.AG + AC.CG = AC (AG + CG) = AC2 Yêu cầu HS đọc đầu bài viết GT – KL Bài ( SBT tr ) : D- BTVN: BT (NCCĐ) ; (SBT)
Tài liệu đính kèm:
 btro8- hinh ki 2.doc
btro8- hinh ki 2.doc





