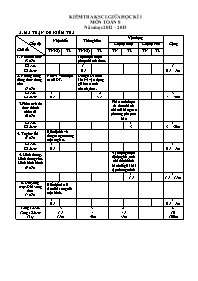
Đề ma trận và kiểm tra khảo sát chất lượng giữa học kì I Toán Lớp 8 - Năm học 2012-2013

KIỂM TRA KSCL GIỮA HỌC KÌ I
MÔN TOÁN 8
Năm học 2012 – 2013 
A. MA TRẬN ĐỀ KIỂM TRA
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TN
TL
TN
TL
1. Nhân đa thức
(3 tiết)
Thực hiện được phép nhân đa thức.
Số câu
1
1
Số điểm
0,5
0,5 = 5%
2. Những hằng đẳng thức đáng nhớ
(5 tiết)
Nhớ và viết được các HĐT.
Dùng HĐT triển khai và vận dụng giải toán tính nhanh, tìm x.
Số câu
1
2
3
Số điểm
0,5
3,5
4 = 40%
3. Phân tích đa thức thành nhân tử
(6 tiết)
Phân tích được đa thức thành nhân tử bằng các phương pháp cơ bản
Số câu 
Số điểm
1
3
1
3 = 30%
4. Tứ giác lồi
(1 tiết)
Biết định lí về tổng các góc trong một tứ giác.
Số câu
1
1
Số điểm
0,5
0,5 = 5%
5. Hình thang. Hình thang cân. Hình bình hành
(9 tiết)
Vận dụng được định nghĩa, tính chất hình bình hành để giải bài tập chứng minh
1
1,5
1
1,5 = 15%
6. Đối xứng trục. Đối xứng tâm
(4 tiết)
Biết thế nào là tâm đối xứng của một hình.
1
0,5
1
0,5 = 5%
Tổng số câu
3
3
2
8
Tổng số điểm
1,5
4
4,5
10
Tỉ lệ
15%
40%
45%
100%
B. Đề bài
Câu1: ( 1điểm )
Làm tính nhân
a) x2 (5x3 – x – 6)
b) ( x2 - 2xy + y2).(x - y)
Câu 2: ( 2 điểm)
Viết các đa thức sau dưới dạng bình phương của một tổng hay một hiêu.
a) y2 + 2y + 1
b) 9x2 + y2 – 6xy
c) 25a2 + 4b2 +20ab
d) x2 – x + 
Câu 3: ( 2 điểm )
 Phân tích các đa thức sau thành nhân tử.
a) 14x2y – 21xy2 + 28x2y2
b) 27x3 - 
c) 3x2 – 3xy - 5x + 5y
d) x2 + 7x + 12
Câu 4: ( 2 điểm )
 Tìm x biết :
a) x(x - 2) + x - 2 = 0
b) 5x(x - 3) – x +3 = 0
Câu 5: ( 3 điểm) 
Cho hình H1 trong đó ABCD là hình bình hành. 
Chứng minh rằng AHCK là hình bình hành.
Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A , O , C thẳng hàng
H1
C. Đáp án – Biểu điểm
Câu
Nội dung
Điểm
1
a)x2 (5x3 – x – 6) = x2 .5x3 – x2.x – x2.6
 = 5x5 – x3 – 6x2
b) ( x2 -2xy + y2 ).( x – y ) = x.( x2 -2xy + y2 ) – y.( x2 -2xy + y2)
 = x3 – 2x2y + xy2 – x2y + 2xy2 – y3 
0,25
0,25
0,25
0,25
2
a) y2 + 2y + 1 = ( y + 1)2 
b) 9x2 +y2 – 6xy = (3x)2 – 2.3xy + y2 
 = (3x – y)2
c) 25a2 +4b2 +20ab = (5a)2 + 2.5 2ab + (2b)2
 = (5a + 2b)2
d) x2 – x + = x2 – 2.x + ()2 
 = (x - )2
0,5
0,25
0,25
0,25
0,25
0,25
0,25
3
a) 14x2y – 21xy2 + 28x2y2 = 7xy( 2x – 3y + 4xy)
b) 27x3 - = (3x)3 – ()3 
 =( 3x - )(9x2 +x + 
c) 3x2 – 3xy - 5x + 5y = (3x2 – 3xy) – (5x +5y)
 = 3x(x –y) - 5(x - y)
 = (x - y)(3x - 5) 
d) x2 + 7x + 12 = x2 + 3x + 4x + 12
 = (x2 + 3x) +(4x +12)
 = x(x +3 ) + 4(x + 3)
 = (x + 3)( x + 4 ) 
0,5
0,25
0,25
0,25
0,25
0,25
0,25
4
a) x(x-2) + x -2 = 0 
 x(x – 2) +(x - 2)
 (x – 2)(x + 1) = 0
Vậy x – 2 = 0 hoặc x + 1 = 0 hay x = 2 hoặc x = -1
b) 5x(x - 3) – x + 3 = 0
 5x(x - 3) – ( x – 3) = 0
 ( x – 3)(5x – 1) = 0
Vậy x – 3 = 0 hoặc 5x – 1 = 0 hay x = 3 hoặc x = 1/5
0,25
0,25
0,5
0,25
0,25
0,5
5
Viết đúng GT, KL 
a) Xét tứ giác AHCK có AH BD và CK BD => AH // CK
xét AHD vàCKB có : 
AD = BC 
Suy ra AHD =CKB ( cạnh huyền - góc nhọn)
=> AH = CK 
Vậy Tứ giác AHCK là hình bình hành
b) Xét hình bình hành AHCK, trung điểm O của đường chéo HK cũng là trung điểm của đường chéo AC ( tính chất đường chéo hình bình hành). Do đó ba điểm A, O , C thẳng hàng
0,5
0,5
0,5
0,5
1
Lưu ý: Học sinh làm cách khác đúng vẫn cho điểm tối đa.