Đề cương ôn tập thi học kì 1 môn Toán 8 theo dạng bài tập - Năm học 2022-2023

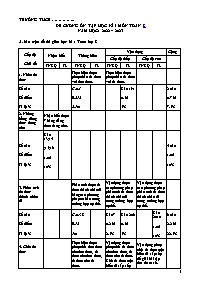
TRƯỜNG THCS ..
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I MÔN TOÁN 8
NĂM HỌC: 2022 – 2023
A. Ma trận đề thi giữa học kì 1 Toán lớp 8
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
1. Nhân đa thức
Thực hiện được phép nhân đa thức với đơn thức.
Thực hiện được phép nhân đa thức với đa thức.
Số câu
Số điểm
Tỉ lệ %
Câu 1
0.25đ
2.5%
Câu 19a
0.5đ
5%
2 câu
0.75đ
7.5%
2. Những hằng đẳng thức đáng nhớ
Nhận biết được 7 hằng đẳng thức đáng nhớ.
Số câu
Số điểm
Tỉ lệ %
Câu 13;14
;15;16
1.0đ
10%
4 câu
1.0đ
10%
3. Phân tích đa thức thành nhân tử
Phân tích được đa thức thành nhân tử bằng các phương pháp cơ bản trong trường hợp cụ thể.
Vận dụng được các phương pháp phân tích đa thức thành nhân tử trong trường hợp cụ thể.
Vận dụng được các phương pháp phân tích đa thức thành nhân tử trong trường hợp cụ thể.
Số câu
Số điểm
Tỉ lệ %
Câu 3;8
0.5đ
5%
Câu 7
0.25đ
2.5%
Câu 20b
0.5đ
5%
Câu 20ac
1.0đ
10%
6 câu
2.25đ
22.5%
4. Chia đa thức 
Thực hiện được phép chia đơn thức cho đơn thức, đa thức cho đơn thức, đa thức cho đa thức.
Vận dụng được phép chia đa thức cho đơn thức, đa thức cho đa thức. Chia đa thức một biến đã sắp xếp
Vận dụng phép chia đa thức một biến đã sắp xếp để giải bài tập tìm tham số.
Số câu
Số điểm
Tỉ lệ %
Câu 2
0.25đ
2.5%
19bc;
1.0đ
10%
Câu 21
0.5đ
5%
4 câu
1.75đ
17.5%
5. Tứ giác
Biết được tổng ba góc của một tứ giác bằng
Số câu
Số điểm
Tỉ lệ %
Câu 6
0.25đ
2.5%
1 câu
0.25đ
2.5%
6. Trục đối xứng. Tâm đối xúng
Hiểu được một hình có trục đối xứng hay không? có tâm đối xứng hay không?.
Vận dụng được các trường hợp bằng nhau của tam giác để xét tính đối xứng của hai hình.
Số câu
Số điểm
Tỉ lệ %
Câu 5
0.25đ
2.5%
Câu 18a
1.25đ
12.5%
2 câu
1.5đ
15%
7. Hình thang. Hình thang cân. Đường trung bình của tam giác, của hình thang
Nhận biết được hình thang cân dựa vào các dấu hiệu nhận biết
Vận dụng công thức tính đường trung bình của tam giác, của hình thang để giải bài tập
Số câu
Số điểm
Tỉ lệ %
Câu 12
0.25đ
2.5%
Câu 4
0.25đ
2.5%
Câu 17
1.0đ
10%
3 câu
1.5đ
15%
8. Hình bình hành
Nhận biết được hình bình hành dựa vào các dấu hiệu nhận biết
Vận dụng được các dấu hiệu nhận biết để chứng minh một tứ giác là hình bình hành
Số câu
Số điểm
Tỉ lệ %
Câu 10
0.25đ
2.5%
Câu 18b
0.25đ
2.5%
2 câu
0.5đ
5%
9. Hình chữ nhật
Nhận biết được hình chữ nhật dựa vào các dấu hiệu nhận biết
Số câu
Số điểm
Tỉ lệ %
Câu 11
0.25đ
2.5%
1 câu
0.25đ
2.5%
10. Hình thoi
Nhận biết được hình thoi dựa vào các dấu hiệu nhận biết
Số câu
Số điểm
Tỉ lệ %
Câu 9
0.25đ
2.5%
1 câu
0.25đ
2.5%
TS câu
TS điểm
Tỉ lệ %
5 câu
1.25đ
12.5%
9 câu
2.25đ
22.5%
2 câu
0.5đ
5%
7 câu
4.5đ
45%
3 câu
1.5đ
15%
26 câu
10đ
100%
B- PHẦN ĐẠI SỐ
I- NHÂN ĐƠN THỨC VỚI ĐA THỨC, ĐA THỨC VỚI ĐA THỨC
Bài 1: Thực hiện phép tính:
 a) 2x(3x2 - 5x + 3)	 	b) -2x2(x2 + 5x - 3) 	c) x2(2x3 - 4x + 3)
 d) (2x - 1)(x2 + 5 - 4)	e) 7x(x - 4) - (7x + 3)(2x2 - x + 4).
Bài 2: Tìm x, biết:
a) 3x(x+1) – 2x(x+2) = -1-x	b) 
c) 	d) x2 +8x + 16 = 0.	
e) 	f) 
II- PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
 Phân tích các đa thức sau thành nhân tử:
a) 14x2y – 21xy2 + 28x2y2	 	b) x(x + y) – 5x – 5y.	
c) 10x(x – y) – 8(y – x).	d) (3x + 1)2 – (x + 1)2	
e) x3 + y3 + z3 – 3xyz	f) 5x2 – 10xy + 5y2 – 20z2.	
g) x3 – x + 3x2y + 3xy2 + y3 – y 	h) x2 + 7x – 8 	
i) x2 + 4x + 3.	j) 16x – 5x2 – 3 	
k) x4 + 4	l) x3 – 2x2 + x – xy2.
III- CHIA ĐA THỨC CHO ĐƠN THỨC, CHIA HAI ĐA THỨC MỘT BIẾN
Bài 1: Làm tính chia:
 a) (6x5y2 - 9x4y3 + 15x3y4) : 3x3y2 	 b) (2x3 - 21x2 + 67x - 60) : (x - 5) 
	c) (6x3 – 7x2 – x + 2) : (2x + 1)	 d) (x2 – y2 + 6x + 9) : (x + y + 3)	
Bài 2: Tìm a, b sao cho: 
a) Đa thức x4 – x3 + 6x2 – x + a chia hết cho đa thức x2 – x + 5
b) Đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
c) Đa thức 3x3 + ax2 + bx + 9 chia hết cho x + 3 và x – 3.
Bài 3: Tìm giá trị nguyên của n 
a) Để giá trị của biểu thức 3n3 + 10n2 – 5 chia hết cho giá trị của biểu thức 3n+1.
 	b) Để giá trị của biểu thức 10n2 + n – 10 chia hết cho giá trị của biểu thức n – 1 .
c) Để đa thức x4 - x3 + 6x2 - x + n chia hết cho đa thức x2 - x + 5
d) Để đa thức 3x3 + 10x2 - 5 chia hết cho đa thức 3x + 1
Bài 4: Chứng minh: 
a) a2( a + 1) + 2a( a + 1) chia hết cho 6 với a Z;	c) x2 + 2x + 2 > 0 với x Z ; 
b) x2 –x + 1 > 0 với x Z ; 	 	d) -x2 + 4x - 5 < 0 với x Z.
Bài 5: Tìm GTLN, GTNN của biểu thức sau:
a) x2 - 6x+11 	b) -x2 + 6x - 11
IV- CÁC PHÉP TOÁN VỀ PHÂN THỨC:
Bài 1 : Thực hiện các phép tính sau : 
	b) + 	 c) + d) 	e) f) + + 
V- CÁC BÀI TOÁN TỔNG HỢP
Bài 1: Cho biểu thức A = 
a) Tìm điều kiện của x để A có nghĩa. b) Rút gọn A. c) Tìm x để A . 
d) Tìm x để biểu thức A nguyên. e) Tính giá trị của biểu thức A khi x2 – 9 = 0
Bài 2: Cho biểu thức B =
a) Tìm ĐKXĐ của B.	b) Rút gọn biểu thức B.
c) Với giá trị nào của a thì B = 0. d) Khi B = 1 thì a nhận giá trị là bao nhiêu ? 
Bài 3: Cho biểu thức 
a) Tìm x để biểu thức C có nghĩa. 	 
b) Rút gọn biểu thức C.	
c) Tìm giá trị của x để giá trị của biểu thức C 
d) Tìm x để giá trị của phân thức C > 0.
Bài 4: Cho phân thức 
a) Tìm ĐKXĐ của D. 	 
b) Hãy rút gọn phân thức D.
c) Tính giá trị của phân thức tại x = 2.	 
d) Tìm giá trị của x để giá trị của phân thức D > 2.
Bài 5: Cho biểu thức 
a) Tìm giá trị của x để giá trị của biểu thức C được xác định. 
b) Tìm giá trị nguyên của x để C nhận giá trị dương.	
c) Tìm x để C = 0.
Bài 6: Cho 
a) Rút gọn biểu thức S. 	 b) Tìm x để giá trị của S = -1
Bài 7: Cho 
a) Tìm điều kiện của x để giá trị của S xác định. 	b) Rút gọn P. 
c) Tính giá trị của S với 	d) Tìm x để giá trị của x để P < 0.
Bài 8: Cho phân thức .
	a) Tìm điều kiện xác định phân thức. 	
b) Tính giá trị của phân thức tại x = - 8.
	c) Rút gọn phân thức. 	
d) Tìm x để giá trị của phân thức nhận giá trị âm.
 Baøi 9: Cho phân thức : P = 
a) Tìm điều kiện của x để P xác định. 	
b) Tìm giá trị của x để phân thức bằng 1
 c) Tìm x để giá trị của phân thức nhận giá trị dương
C- PHẦN HÌNH HỌC
Bài 1: Cho hình chữ nhật ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của các cạnh AB, CD.Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.
 a) Tứ giác ADFE là hình gì? Vì sao ? 	
 b) Chứng minh EMFN là hình vuông.
Bài 2: Cho tam giac ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm AC, K là điểm đối xứng với M qua I.
 	a) Tứ giác AMCK là hình gì? Vì sao? 
b) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông.
Bài 3: Cho tam giác ABC vuông tại A đường cao AH. Gọi D là điểm đối xứng với H qua AC. Chứng minh: 
 	a) D đối xứng với E qua A. 	 	b) Tam giác DHE vuông.
 c) Tứ giác BDEC là hình thang vuông. 	d) BC = BD + CE
Bài 4: Cho hình thoi ABCD, O là giao điểm hai đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, hai đường thẳng đó cắt nhau tại K. 
 a) Tứ giác OBKC là hình gì? Vì sao?	
b) Chứng minh: AB = OK.
 c) Tìm điều kiện của tứ giác ABCD để tứ giác OBKC là hình vuông. 
Bài 5: Cho DABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của M qua I.
	a) Tứ giác AMCK là hình gì? Vì sao?	
	b) Tứ giác AKMB là hình gì? Vì sao?
 c) Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh tứ giác ABEC là hình thoi.
Bài 6: Cho hình bình hành ABCD có AD = 2AB, . Gọi E và F lần lượt là trung điểm của BC và AD.
a) Chứng minh AEBF.
b) Chứng minh tứ giác BFDC là hình thang cân.
c) Lấy điểm M đối xứng của A qua B. Chứng minh tứ giác BMCD là hình chữ nhật.
d) Chứng minh M, E, D thẳng hàng. 
Bài 7: Cho tam giác ABC vuông tại A có , kẻ tia Ax song song với BC. Trên Ax lấy điểm D sao cho AD = DC.
a). Chứng minh tứ giác ABCD là hình thang cân.
b) Gọi E là trung điểm của BC. Chứng minh tứ giác ADEB là hình thoi.
c) Cho AC = 8cm, AB = 5cm. Tính diện tích hình thoi ABED
MỘT SỐ ĐỀ THAM KHẢO
ĐỀ 1
Bài 1: Thực hiện phép tính:
 	b) 
c) 	d) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
5x – 10xy	b) x2 + 2xy + y2 – 9z2	c) 3x2 – 2x – 5 
Bài 3: Tìm x, biết:
 	b) 
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức P được xác định.
Rút gọn P.
Bài 5: Cho ABC vuông tại A, biết AB = 6cm, AC = 8cm. Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
Tính AI.
Chứng minh tứ giác AMIN là hình chữ nhật.
Gọi D là điểm đối xứng của I qua N. chứng minh tứ giác ADCI là hình thoi.
Đường thẳng BN cắt DC tại K. Chứng minh DC = 3DK.
Bài 6: Cho x, y thỏa mãn 
Tính giá trị của biểu thức 
----------------------------------------------------------------
ĐỀ 2 
Bài 1: Thực hiện phép tính:
 	b) 
 	d) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
 	b) 
Bài 3: Tìm x, biết:
 	b) 
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức P được xác định.
Rút gọn P.
Bài 5: Cho ABC vuông tại A có AB < AC.Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
Chúng minh tứ giác BFCE là hình bình hành.
Chứng minh tứ giác BFEA là hình chữ nhật.
Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
Vẽ AH BC tại H. Gọi M là trung điểm của HC. Chứng minh FM AM.
Bài 6:
Cho a, b, c là độ dài ba cạnh của một tam giác. Chứng minh 
----------------------------------------------------------------------
ĐỀ 3 
Bài 1: Thực hiện phép tính:
 	b) 
 	d) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
 	b) 	c) 
Bài 3: Tìm x, biết:
 	b) 
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức P được xác định.
Rút gọn P.
Bài 5: Cho ABC vuông tại A. Vẽ AH BC tại H. Biết AB = 15cm, BC = 25cm.
Tính AC và diện tích tam giác ABC.
Từ H vẽ HM AB tại M, HN AC tại N. Chứng minh tứ giác AMHN là hình chữ nhật.
Trên tia đối của tia AC lấy điểm D sao cho AD = AN. Chứng minh tứ giác ADMH là hình bình hành.
Gọi K là điểm đối xứng của B qua A. Gọi I, E lần lượt là trung điểm của AH và BH. Chứng minh CI HK.
Bài 6: Cho a + b = 1. Tính giá trị của các biểu thức sau:
------------------------------------------------------------------
ĐỀ 4
Bài 1: Thực hiện phép tính:
a) 	b) 
c) 	d) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
a) 	b) 	
Bài 3: Tìm x, biết: 	
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức M được xác định.
Rút gọn M.
Bài 5: Cho ABC vuông tại A có AB < AC. Gọi D là trung điểm của BC. Vẽ DE AB tại E, DF AC tại F. 
Chứng minh tứ giác AEDF là hình chữ nhật.
Gọi M là điểm đối xứng của D qua F. Chứng minh tứ giác ADCM là hình thoi.
Chứng minh tứ giác ABDM là hình bình hành.
Đường thẳng BF cắt MC tại N. Chứng minh 
Bài 6: Cho và a + b + c = abc. Tính giá trị của biểu thức sau: 
---------------------------------------------------
ĐỀ 5 
Bài 1: Thực hiện phép tính:
a) 	b) 
c) 	d) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
a) 	b) 	
Bài 3: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức A được xác định.
Rút gọn A.
Bài 4: Cho ABC vuông tại A có đường cao AH. Từ H kẻ HM AB (M AB), HN AC 
(N AC). Gọi D là điểm đối xứng với H qua M, E là điểm đối xứng với H qua N. Chứng minh:
Tứ giác AMHN là hình chữ nhật.
Tứ giác AMNE là hình bình hành.
A là trung điểm của DE.
BC2 = BD2 + CE2 + 2.BH.HC
Bài 5: Cho xyz = 1. Tính tổng 
-------------------------------------------------------
ĐỀ 6
Bài 1: Thực hiện phép tính:
a) 	b) 
Bài 2: Phân tích các đa thức sau thành nhân tử:	
a) 	b) 	
Bài 3: Thực hiện phép tính:
a) 	b) 
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức A được xác định.
Rút gọn A.
Bài 5: Cho tam giác ABC vuông tại A. Từ trung điểm M của cạnh BC kẻ MD AB, ME AC 
Chứng minh tứ giác ADME là hình chữ nhật.
Gọi F là điểm đối xứng của M qua E. Chứng minh tứ giác AFCM là hình thoi.
Gọi O là trung điểm của AM. Chứng minh ba điểm B, O, F thẳng hàng.
Biết AC = 16cm, BC = 20cm. Tính diện tích hình chữ nhật ADME.
Bài 6: Cho chứng minh rằng x = y = z
ĐỀ 7
Bài 1: Thực hiện phép tính:
a) 	b) 
Bài 2:
a) Phân tích các đa thức sau thành nhân tử: 	
b) Tìm x, biết: 	
Bài 3: Thực hiện phép tính:
a) 	b) 
Bài 4: Cho biểu thức: 
Tìm điều kiện của x để giá trị của biểu thức A được xác định.
Rút gọn A.
Bài 5: Cho hình chữ nhật ABCD. Từ A vẽ AH BD (H BD). Gọi I, K, F theo thứ tự là trung điểm của AH, BH, CD.
Chứng minh KI // AB.
Chứng minh tứ giác DIKF là hình bình hành.
Chứng minh .
Tính diện tích tam giác AKB biết AB = 20cm, AD = 15cm.
Bài 6: Xác định các số a và b để đa thức x3 + ax + b chia hết cho đa thức x2 + x – 2.
---------------------HẾT--------------------------