Thiết kế giáo án Hình học 8 - Tiết 21 đến tiết 25

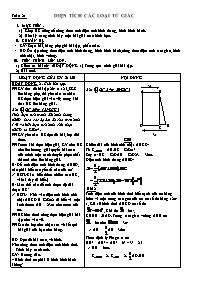
Tuần 21 DIỆN TÍCH CÁC LOẠI TỨ GIÁC
MỤC TIÊU.
Giúp HS củng cố công thức tính diện tích hình thang, hình bình hành.
Rèn kỹ năng trình bày một bài giải toán hình học. 
CHUẨN BỊ.
GV: Soạn bài, bảng phụ ghi bài tập, phấn màu. 
HS: Ôn tập công thức diện tích hình thang, hình bình hành,công thức diện tích tam giác, hình chữ nhật, hình vuông.
TIẾN TRÌNH LÊN LỚP.
Kiểm tra bài cũ: (HOẠT ĐỘNG 1) Trong quá trình giải bài tập.
Bài mới.
HOẠT ĐỘNG CỦA GV & HS
NỘI DUNG
HOẠT ĐỘNG 2 . Giải bài tập.
GV đưa đề bài tập 26/ tr 125_SGK lên bảng phụ, rồi yêu cầu cá nhân HS thực hiện giải vào vở; trong khi đó 1 HS lên bảng giải .
Bài (BT 26/tr 125-SGK)
Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là 828m2.
GV yêu cầu HS đọc đề bài, lớp dõi theo.
Trước khi thực hiện giải, GV cho HS nêu lên hướng giải quyết bài toán của mình một cách thuyết phục nhất thì mới cho lên bảng giải.
H: Để tính diện tích hình thang ABED, cần phải biết các yếu tố nào của nó?
HSTL:Cần biết thêm chiều cao BC, vì hai đáy đã biết.)
H: Làm thế nào để tính được độ dài đoạn BC?
HSTL: Nhờ vào diện tích hình chữ nhật ABCD là 828m2 đã biết và một kích thước AB = 23m cho trước của nó.
HS bên dưới cùng thực hiện giải bài tập trên vào vở.
Sau đó lớp nêu nhận xét về kết quả bài giải của bạn trên bảng.
HS: Đọc đề bài toán, vẽ hình.
Nêu công thức tính diện tích hình thoi.
+ Trình bày cách tính.
GV: Hướng dẫn.
* Hình thoi có phải là hình bình hành không?
 + Có thể dùng công thức tính diện tích hình bình hành để tính diện tích hình thoi không?
+ Cách 2: đều nên BD = 6 cm
Áp dụng định lí Pitago. Ta có : AC = 10cm.
Từ đó suy ra diện tích hình thoi.
GV: Hướng dẫn học sinh vẽ hình, phân tích hình vẽ. Tìm hướng giải bài toán.
Nhận xét gì về hình bình hành và tam giác.
+ Tìm chiều cao chung của hình bình hành và tam giác?
HS: Nêu .
So sánh DE và EC?
HS: Thảo luận nhóm, tính diện tích cử đại diện trình bày bài giải.
Lớp nhận xét bổ sung.
GV: Sửa chữa, củng cố.
A
B
E
D
C
31m
23m
Bài (BT 24/tr 20-SBT) 
 Giải
Chiều dài của hình chữ nhật ABCD:
Từ SABCD = AB.BC = 828m2
Suy ra: BC = 828:AB = 828:23 = 36m.
Diện tích hình thang ABED:
 Bài 2
Tính diện tích của hình thoi biết cạnh của nó bằng 6dm và một trong các góc của nó có số do bằng 120o 
a, Giả sử hình thoi ABCD có số đo 
 , Khi đó = 60o, 
Kẻ BH AD. Trong tam giác vuông ABH có 
 = 60 nên = 30o
 => AH = AB = 3dm
Theo định lý Pitago ta có 
BH2 = AB2 – AH2 = 62 – 32 = 25
=> BH = 5cm.
SABCD = 2. SABD = 2. AD.BH 
 = 2. 6.5= 30(cm2)
Bài 3
Cho hình thang ABCD (AB//CD) có AB = 6cm, đường cao bằng 9cm. Đường thẳng đi qua B song song với AD cắt CD tại E chia hình thang ABCD thành hình bình hành ABED và tam giác BEC có diện tích bằng nhau.
Tính diện tích hình thang?
a, Tứ giác ABED có các cạnh đối song song nên ABED là hình bình hành, do đó:
SABED = DE.BH; SBCE = EC.BH.
Do SABED = SBCE nên 
DE.BH = EC.BH => CE = 2DE. 
Ta lại có DE = AB = 6cm, do đó CE = 2DE = 12cm và 
CD = CE + ED = 18cm.
SABCD = (AB + CD).BH 
= (6 + 18).9 = 98(cm2)
Vận dụng-Củng cố: (HOẠT ĐỘNG 3 )
GV yêu cầu HS nhắc lại công thức tính diện tích các hình tam giác, chữ nhật, hình thang, hình bình hành.
4) BTVN : Cho tam giác ABC trung tuyến AD. Gọi I là trung điểm của AD. Tia CI cắt AB tại M.Gọi N là trung điẻm của MB. Biết diện tích tam giác ABC bằng 36m2. Tính diện tích tam giác BNC?
Tuần 22 Phương trình đưa được về dạng ax+b = 0 .
 I. Mục tiêu bài dạy:
Rèn kĩ năng giải phương trình, biến đổi tương đương các phương trình.
Học sinh thực hành tốt giải các phương trình đưa được về dạng ax + b = 0 II CHUẨN BỊ.
GV: Soạn bài, bảng phụ ghi bài tập, phấn màu. 
HS: Ôn tập các dạng phương trình đưa được về phương trình bậc nhất.
 III TIẾN TRÌNH LÊN LỚP.
1) Kiểm tra bài cũ: Trong quá trình giải bài tập.
2) Bài mới.
Hoạt động của thầy và trò
Nội dung
GV treo bảng phụ ghi đề bài tập 1
Hs quan sát đọc đề suy nghĩ tìm cách làm
+ Gọi 1 hs nêu cách làm
+ Gọi hs khác nhận xét bổ sung
+ Để ít phút để học sinh làm bài.
GV: Gọi 2 hs lên bảng trình bày lời giải. Lớp nhận xét bổ sung
GV: Sửa chữa, nhận xét bổ sung.
Bài tập 1: 
Giải các phương trình sau:
a)4x(2x + 3) - x(8x - 1) = 5(x + 2)
b)(3x - 5)(3x + 5) - x(9x - 1) = 4
Giải:
a)4x(2x + 3) - x(8x - 1) = 5(x + 2)
Û 8x2 + 12x - 8x2 + x = 5x + 10
Û 8x2 - 8x2 + 12x + x - 5x = 10
Û 8x = 10
Û x = 1,25
b)(3x - 5)(3x + 5) - x(9x - 1) = 4
Û 9x2 - 25 - 9x2 + x = 4
Û 9x2 - 9x2 + x = 4 + 25
Û x = 29
GV ghi đề bài tập 2
Hs quan sát đọc đề suy nghĩ tìm cách làm
GV: Nêu các bước giải các phương trình trên.
 HS: Nêu các bước giải . Lớp nhận xét bổ sung.
GV: Phân tích các dạng và cách giải của mỗi dạng.
+ Gọi 3 học sinh giải bài tập.
Cả lớp cùng giải. 
GV: Hướng dẫn.
Lớp nhận xét bổ sung.
GV: Sửa chữa, củng cố bài học.
Bài tập 2: 
Giải các phương trình sau:
a)3 - 4x(25 - 2x) = 8x2 + x - 300
Giải:
a)3 - 4x(25 - 2x) = 8x2 + x - 300
Û3 - 100x + 8x2=8x2 + x - 300
Û8x2 - 8x2 - 100x - x = -300 - 3
Û -101x = -303
Û x = 3
Û 8(1 - 3x) - 2(2 + 3x)=140 - 15(2x + 1)
Û 8 - 24x - 4 - 6x = 140 - 30x - 15
Û - 24x - 6x + 30x = 140 - 15 - 8 + 4
Û 0x = 121
Vậy phương trình vô nghiệm.
Û 5(5x + 2) - 10(8x - 1) = 6(4x + 2) - 150
Û 25x + 10 - 80x + 10 = 24x + 12 - 150
Û 25x - 80x - 24x = 12 - 150 - 10 - 10
Û - 79x = - 158
Û x = 2
HĐ3: Củng cố.
V.Hướng dẫn về nhà:
Nắm chắc các phép biến đổi tương đương các phương trình và cách làm các dạng bài tập trên.
Bài tập về nhà: Gi¶i ph­¬ng tr×nh:
a, 5(2x - 3) - 4(5x - 7) = 19 - 2(x + 11)
b, 17 - 14(x + 1) = 13 - 4(x + 1) -5(x - 3)
c, 
d, 
Tuần 23 Tên bài dạy: GIẢI PHƯƠNG TRÌNH CHỨA ẨN Ở MẪU. 
 I/Mục tiêu bài học: Qua bài này học sinh cần nắm:
Giúp HS củng cố về cách giải phương trình chứa ẩn ở mẫu, qua đó HS nắm vững hơn trình tự giải và ý nghĩa cụ thể của từng bước giải.
Rèn kỹ năng vận dụng vào giải các bài tập liên quan
 II/Chuẩn bị của giáo viên và học sinh:
 1/Đối với giáo viên: Bài soạn,thước thẳng,phấn màu, MTBT
 2/Đối với học sinh: Tìm hiểu nội dung bài học, thước, MTBT.
 3/Đối với nhóm học sinh:Phiếu học tập.
 IIICác hoạt động dạy và học:	
Hoạt động của thầy và trò
Nội dung ghi bảng
Hoạt động1: Ôn tập lý thuyết
GV: Nêu các bước giải phương trình chứa ẩn ở mẫu?
HS: Nêu các bước giải phương trình chứa ẩn ở mẫu.
GV: Củng cố các bước giải.. Chú ý học sinh bước xác định ĐK cho ẩn và bước chọn nghiệm.
Cách giải phương trình chứa ẩn ở mẫu 
 Bước 1:Tìm điều kiện xác định của PT.
 Bước 2:Qui đồng mẫu hai vế và khử mẫu.
 Bước 3 : Giải PT vừa nhận được .
 Bước 4 : Chọn nghiệm.
Hoạt động2: LUYỆN TẬP
GV đưa đề bài tập BT 38/tr9-SBT lên bảng phụ, rồi yêu cầu cá nhân HS thực hiện giải vào vở; trong khi đó chọn 1 HS lên bảng giải: 
Bài BT 38/tr9-SBT 
Giải các phương trình sau:
GV yêu cầu HS nêu điều kiện xác định của phương trình a); mẫu thức chung của cả hai vế của phương trình.
HSTL: . . . MTC là x + 1 
Tương tự, GV yêu cầu HS phải xác định ĐKXĐ và mẩu thức chung ở hai vế của mỗi phương trình b, c và d trước khi thực hiện giải.
GV thường xuyên lưu ý nhắc nhở HS có thói quen chỉ sử dụng dấu Þ ngay sau khi khử mẫu.
GV: Sửa chữa, củng cố các bước giải phương trình chứa ẩn ở mẫu.
Bài (BT 39/tr10-SBT)
GV đưa đề bài trên bảng phụ.
 a). Tìm x sao cho giá trị của biểu thức 
 bằng 2.
H: Để giải bài toán này, ta cần phải làm gì?
HSTL: Cần lập phương trình với vế phải bằng 2: ; rồi giải phương trình vừa lập được.
GV chọn 1 HS lên bảng giải, lớp làm vào vở.
GV đặt câu hỏi tương tự đối với các câu b và c.
HSTL: Tương tự cách thực hiện như ở câu a), ta phải lập phương trình biểu thị sự bằng nhau của hai biểu thức; rồi giải phương trình lập được, cuối cùng là nhận xét kết quả và trả lời cho bài toán.
GV chọn hai HS lên bảng giải câu b) và c): Mỗi em một câu.
Bài BT 38/tr9-SBT 
Þ 2x + 4 = 2x + 3
Û 0x = – 1 
Không có giá trị nào của x thỏa mãn hệ thức.
Vậy S = Æ
Vậy S = Æ
 ( Thỏa mãn ĐKXĐ)
(ĐKXĐ: )
Bài (BT 39/tr10-SBT)Tìm x thỏa mãn:
 (ĐKXĐ: x ≠ )
Vậy không tồn tại giá trị nào của x thỏa mãn điều kiện của bài toán.
Vậy với x = thì hai biểu thức đã cho bằng nhau.
Hoạt động 3: Hướng dẫn về nhà
Nắm vững các bước giải phương trình chứa ẩn ở mẫu + BT 40; 41/tr 10_SBT
Tuần 24 Tên bài dạy: ĐỊNH LÍ TA - LÉT VÀ HỆ QUẢ. 
 I/Mục tiêu bài học: Qua bài này học sinh cần nắm:
 Củng cố định lí và hệ quả của định lí Talet. 
 Vận dụng định lí tính độ dài đoạn thẳng, chứng minh đường thẳng song song, bước đầu sử dụng tính chất của dãy tỉ số bằng nhau trong giải toán hình học.
	Rèn luyện tính cẩn thận, chính xác, tư duy linh hoạt.
 II/Chuẩn bị của giáo viên và học sinh:
1/Đối với giáo viên: Bài soạn,thước thẳng,phấn màu, MTBT
 2/Đối với học sinh: Tìm hiểu nội dung bài học, thước, MTBT.
 3/Đối với nhóm học sinh:Phiếu học tập.
 III/Các hoạt động dạy và học:	
Hoạt động của thầy
Hoạt động của trò
Hoạt động1: Ôn tập lý thuyết
GV: Phát biểu nội dung định lí Ta lét thuận và đảo?
+ Nêu các tính chất của tỉ lệ thức?
HS: Phát biểu.
GV: Ghi bảng, củng cố.
1) ABC :
(hoặc; )
2) Một vài tính chất của tỉ lệ thức:
Hoạt động 2: LUYỆN TẬP
GV: Ghi đề bài.
+ HS đọc đề, lên bảng vẽ hình, ghi GT, KL.
GV: Để chứng minh MN // BC. Ta cần chứng minh điều gì?
+ Phát biểu nội dung định lí Talet thuận và đảo?
HS: Phát biểu định lí, nêu cách chứng minh
GV: Gọi học sinh chứng minh. Lớp nhận xét bổ sung.
GV: Sửa chữa, củng cố cách chứng minh đường thẳng song song bằng đ/lí Talet đảo.
+ Tính độ dài đoạn thẳng MN?
+ Nêu các dãy tỉ số để tính MN?
à Tính MN.
HS: Trình bày bài giải.
GV: Sửa chữa, củng cố bài học.
GV: Ghi đề bài tập.
HS: Đọc đề, vẽ hình và ghi GT - KL
+ GV gợi ý: Kéo dài DA và CB cắt nhau tại E. Áp dụng định lí Talet vào EMN và EDC.
+ Xét EMN: AB // MN; EDC: 
AB //DC. Viết các tỉ số bằng nhau của các đoạn thẳng tỉ lệ?
HS: Viết, so sánh tìm ra tỉ lệ thức cần chứng minh.
* Phát biểu các tính chất của dãy tỉ số bằng nhau đã học ở lớp 7?
HS: Phát biểu.
GV: Ghi bảng hướng dẫn học sinh giải bài tập. Phân tích để học sinh thấy rõ các tính chất đã áp dụng.
 Bài 1: Cho rABC có AB= 15cm, AC =12cm, và BC = 20cm. Trên hai cạnh AB, AC lấy hai điểm M và N sao cho AM = 5cm, CN = 8cm.
a) Chứng minh : MN // BC
b) Tính độ dài đoạn thẳng MN.
Chứng minh
a) AN = AC – CN = 12 – 8 = 4 (cm)
Ta có: 
Do đó: => MN // BC (Đlí đảo)
b) MN // BC => hay 
Bài 2: Cho hình thang ABCD có AB // CD và 
AB < CD. Đường thẳng song songvới đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng: 
Chứng minh
a) MN // AB // CD (gt)
Kéo dài DA và CB cắt nhau tại E.
Áp dụng định lí Talet vào rEMN và rEDC ta được: 
Từ (1) và (2) => (3)
b) Từ (3), áp dụng tính chất dãy tỉ số bằng nhau ta được: 
 => 
 => (4)
c) Từ (4) => 
 hay 
Hoạt động 3: Hướng dẫn về nhà
4 Nắm vững nội dung định lí Ta let thuận và đảo, hệ quả của định lí Talet.
Bài tập : Cho tam giác ABC, Trên cạch AB và AC lần lượt lấy 2 điểm M và N. Biết 
AM = 3cm, MB = 2cm, AN = 7,5cm, NC = 5cm
a, Chứng minh MN//BC
b, Gọi I là trung điểm của BC, K là giao điểm của AI với MN. Chứng minh K là trung điểm của MN 
Tuần 25 Tên bài dạy: TÍNH CHẤT ĐƯỜNG PHÂN GIÁC TRONG TAM GIÁC 
I/Mục tiêu bài học: Qua bài này học sinh cần nắm:
+ Củng cố tính chất phân giác của tam giác.
•	Rèn luyện tính cẩn thận, chính xác, tư duy linh hoạt.
 B/Chuẩn bị của giáo viên và học sinh:
 1/Đối với giáo viên: Bài soạn,thước thẳng, compa,phấn màu, MTBT
 2/Đối với học sinh: Tìm hiểu nội dung bài học, thước, MTBT.
 II/Các hoạt động dạy và học:	
Hoạt động của thầy
Hoạt động của trò
Hoạt động1: Ôn tập lý thuyết
1Ôn tập tính chất đường phân giác trong tam giác: 
rABC có AD là đường phân giác 
thì 
HS: phát biểu tính chất đường phân giác trong tam giác.
+ Vẽ hình, ghi biểu thức minh họa .
Hoạt động2: LUYỆN TẬP
BÀI 1: Cho rABC (Â = 900), AB = 21cm, AC = 28cm, đường phân giác của góc A cắt BC tại D, đường thẳng qua D song song với AB cắt AC tại E. Â)Tính độ dài các đoạn thẳng BD, DC, DE.
b)Tính diện tích rABD và diện tích rACD?
Giải: 
a) Â = 900 
=> BC2 = AB2 + AC2 (định lí pytago) 
hay BC2 = 212 + 282 = 1225 => BC = 35 (cm)
* Ta có: 
=> 
 DC = BC – BD = 35 – 15 = 20 (cm)
* = 12 cm
b) SADC = = 168 (dm2)
 SABD = SABC -SADC = 126 dm2
BÀI 2: Cho rABC có chu vi bằng 74 dm.
Đường phân giác BD chia cạnh AC thành hai đoạn thẳng tỉ lệ với 2 và 3. Đường phân giác của góc C chia cạnh AB thành hai đoạn thẳng tỉ lệ với 4 và 5. Tính độ dài 3 cạnh của rABC?
Giải : Áp dụng tính chất đường phân giác trong tam giác. Ta có :
* ; 
Suy ra : 
AB= 20dm; BC = 30dm; AC = 24dm.
GV: Ghi đề bài toán, vẽ hình. Hướng dẫn học sinh các bước thực hiện tính độ dài các đoạn thẳng?
 + Viết biểu thức đường phân giác của góc A.
+ Từ , suy ra cách tính độ dài BD; DC?
+ Áp dụng định lí Talet cho DE // AB, ta có điều gì?
HS: Trình bày các bước tính.
Lớp nhận xét bổ sung.
GV: Sửa chữa, củng cố bài học.
GV: Ghi đề bài toán. 
HS: Vẽ hình, phân tích bài toán. Tìm cách tính.
GV: Hướng dẫn:
+ Viết biểu thức đường phân giác của góc B và góc C?
+ Từ chu vi của rABC bằng 74 dm.
Ta suy ra điều gì?
+ Viết biểu thức liên hệ giữa hai tỉ lệ thức trên?
HS: Trình bày các bước giải.
GV: Sửa chữa, củng cố tính chất.
Hoạt động3: Hướng dẫn về nhà
Xem lại các bài tập đã giải, nắm vững tính chất đường phân giác trong tam giác.
Tuần 26 Tên bài dạy: GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH 
 I/Mục tiêu bài học: Qua bài này học sinh cần nắm:
 Các bước giải bài toán bằng cách lập phương trình, kỹ năng chọn ẩn và biễu diễn các số liệu chưa biết qua ẩn. Lập và giải phương trình, chọn nghiệm và trả lời.
Rèn luyện tính cẩn thận, chính xác, tư duy linh hoạt.
 B/Chuẩn bị của giáo viên và học sinh:
 1/ Giáo viên: Bài soạn,thước thẳng, phấn màu, MTBT
 2/ Học sinh: Tìm hiểu nội dung bài học, thước, MTBT.
 3/ Nhóm học sinh:Phiếu học tập.
II/Các hoạt động dạy và học:	
Hoạt động của thầy
Hoạt động của trò
Hoạt động1: Ôn tập lý thuyết
* Bước 1. Lập phương trình:
 - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
 - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
 - Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
*Bước 2. Giải phương trình.
*Bước 3. Trả lời: kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện của ẩn, nghiệm nào không rồi kết luận.
Gv: Nêu các bước giải bài toán bằng cách lập phương trình?
HS: Nêu các bước giải.
Gv: củng cố các bước giải bài toán bằng cách lập phương trình.
Hoạt động2: LUYỆN TẬP
Bài 1: Hai vòi nước cùng chảy vào một bể cạn, mất h mới đầy bể. Nếu chảy riêng thì mỗi vòi phải mất bao nhiêu thời gian mới chảy đầy bể ? Cho biết năng suất vòi I bằng năng suất của vòi II
Giải Gọi x là năng suất của vòi I . 
 ĐK: x > 0; phần bể.
Năng suất cả hai vòi: phần bể.
Năng suất vòi 2: - x phần bể.
Vì năng suất vòi I bằng năng suất vòi 2.
Ta có phương trình : x = .( - x )
Giải phương trình . 
Ta có nghiệm: x = ( thỏa mãn)
Vậy thời gian chảy một mình đầy bể nước + Vòi I : = 8h ; Vòi II : 12h.
Bài 2: Một người đi xe đạp từ A đến B với vận tốc 12km/giờ, rồi quay về A với vận tốc 10km/giờ . Cả đi và về mất 4 giờ 24 phút. Tìm chiều dài quãng đường AB
Gọi x là chiều dài quãng đường AB. 
 ( x>0, Km) 
 Lập bảng 
Quãng đường
(Km)
Vận tốc
(Km/giờ)
Thời gian
(Giờ)
Từ
AB
x
12
 Tư 
BA
x
10
 Theo bài toán, ta có phương trình : 
 + = 
 Giải phương trình, chọn nghiệm và trả lời 
 x = 24 ( Thõa mãn)
 Vậy quãng đường AB dài 24 Km. 
Gv: Giới thiệu bài tập.
HS: Đọc đề bài tập. Phân tích bài toán.Nêu cách chọn ẩn và các bước giải bài toán.
Gv: Gọi 2 học sinh giải bài toán bằng 2 cách :
Đặt ẩn trực tiếp và gián tiếp. Lớp nhận xét bổ sung.
Gv: Sửa chữa, chú ý học sinh công thức giải bài toán năng suất : N.t = 1
Gv : Giới thiệu bài toán.
HS: Thảo luận nhóm, giải bài tập.
Gv: Hướng dẫn 
+ Thu phiếu học tập các nhóm, phân tích sửa chữa.
Chú ý:
+ Trong một bài toán có nhiều cách đặt ẩn khác nhau .
+ Với cùng một cách đặt ẩn, có nhiều cách biểu diễn các số liệu khác nhau.
HS: Phân tích các cách giải các nhóm để hiểu rõ các bước giải bài toán bằng cách lập phương trình.
Hoạt động3: Hướng dẫn về nhà
Tính tuổi của An và mẹ An biết rằng cách đây 3 năm tuổi của mẹ An gấp 4 lần tuổi An và sau đây hai năm tuổi của mẹ An gấp 3 lần tuổi An
Tuần 25 Tên bài dạy: Ôn tập các trường hợp đồng dạng của tam giác. 
 I/Mục tiêu bài học: Qua bài này học sinh cần nắm:
Củng cố trường hợp đồng dạng thứ I và thứ II của hai tam giác. Kỹ năng nhận biết và chứng minh hai tam giác đồng dạng.
Rèn luyện tính cẩn thận, chính xác, tư duy linh hoạt.
 B/Chuẩn bị của giáo viên và học sinh:
1/Đối với giáo viên: Bài soạn,thước thẳng, phấn màu, MTBT
 2/Đối với học sinh: Tìm hiểu nội dung bài học, thước, MTBT.
 3/Đối với nhóm học sinh:Phiếu học tập.
 II/Các hoạt động dạy và học:	
Hoạt động của thầy
Hoạt động của trò
Hoạt động1: Ôn tập lý thuyết
1) Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
2)Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó băng nhau thì hai tam giác đồng dạng.
+ Phát biểu trường hợp đồng dạng thứ nhất của hai tam giác?
+ Phát biểu trường hợp đồng dạng thứ II của hai tam giác?
Hoạt động2: LUYỆN TẬP
BÀI 1: rABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R theo thứ tự là trung điểm của các đoạn thẳng OA, OB, OC. Chứng minh rằng rPQR rABC
Giải: Theo giả thiết ta có:
 PQ là đường trung bình của rOAB 
=> PQ = => 
 QR là đường trung bình của rOBC 
=> QR = => 
 PR là đường trung bình của rOAC 
=> PR = => (3)
 Từ (1), (2) và (3) => 
Suy ra : rPQR rABC (c.c.c) với tỉ số đồng dạng k = 
Bài 2: Cho rABC có AB = 10 cm, AC = 20 cm. Trên tia AC đặt đoạn thẳng AD = 5 cm. Chứng minh rằng .
Giải: 
Xét r ADB và r ABC có :
Suy ra : (1)
Mặt khác, Â góc chung (2)
Từ (1) và (2) suy ra : r ADB r ABC 
=> 
HS: Đọc đề bài toán, vẽ hình.
Gv: Hướng dẫn chứng minh:
+So sánh các tỉ số , , ?
+ Xét quan hệ giữa PQ và AB?...
HS: Trình bày chứng minh.
Gv: Sửa chữa, củng cố các bước chứng minh tam giác đồng dạng.
HS: Đọc đề bài toán, vẽ hình ghi giả thiết, kết luận.
Gv: Chứng minh: ?
+ Nhận xét gì về r ADB và r ABC
+ Xét và ?
HS:Thảo luận nhóm, tìm cách chứng minh.
Gv: Gọi đại diện nhóm trình bày bài giải.
+ Các nhóm khác nhận xét bổ sung.
Gv: Sửa chữa, củng cố bài học.
Hoạt động3: Hướng dẫn về nhà
Bài tập về nhà: Cho , hai đường cao AA1 và BB1 . 
Chứng minh : ?
Hướng dẫn vẽ hình: