Thiết kế bài giảng Hình học Lớp 8 - Tiết 35+36+37
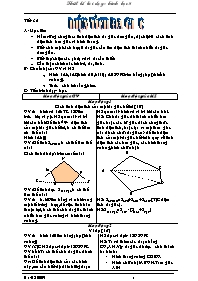
Cách tính diện tích của một đa giác bất kì (10)
GV đưa hình vẽ 148 TR 129 lên trước lớp và y/c HS quan sát và trả lời câu hỏi: Để tính được diện tích của một đa giác bất kì, ta có thể làm như thế nào?
Hình 148(a)
GV: Để tính SABCDE ta có thể làm thế nào?
Cách tính đó dựa trên cơ sở nào?
GV: Để tính được SMNPQR ta có thể làm thế nào?
GV đưa h.149 lên bảng và nói: trong một số trường hợp, để việc tính toán thuận lợi, ta có thể chia đa giác thành nhiều tam giác vuông và hình thang vuông. HS quan sát hình vẽ và trả lời câu hỏi.
HS: Chia đa giác đó thành nhiều tam giác hoặc các tứ giác đã có công thức tính diện tích, hoặc tạo ra một tam giac nào đó có chứa đa giác=> để tính diện tích của một đa giác bất kì ta quy về tính diện tích các tam giác, các hình thang vuông, hình chữ nhật.
HS: SABCDE=SABC+SACD+SADE.(T/C diện tích đa giác).
HS:SMNPQR=SNST-(SMRS+SPQT)
Tiết 35 A- Mục tiêu Nắm vững công thcs tính diện tích đa giác đơn giản, đặc biệt là cách tính diện tích tam giác và hình thang. Biết chia một cách hợp lí đa giác cần tìm diện tích thành nhiều đa giác đơn giản. Biết thực hiện các phép vẽ và đo cần thiết. Cẩn thận chính xác khi vẽ, đo, tính. B- Chuẩn bị của GV và HS Hình 148, 149, hình 50, bài tập 40 SGK trên bảng phụ(có kẻ ô vuông). Thước chia khoảng, ê ke. C- Tiến trình dạy- học Hoạt động của GV Hoạt động của HS Hoạt động 1 Cách tính diện tích của một đa giác bất kì (10’) GV đưa hình vẽ 148 TR 129 lên trước lớp và y/c HS quan sát và trả lời câu hỏi: Để tính được diện tích của một đa giác bất kì, ta có thể làm như thế nào? Hình 148(a) GV: Để tính SABCDE ta có thể làm thế nào? Cách tính đó dựa trên cơ sở nào? M Q R P T S N GV: Để tính được SMNPQR ta có thể làm thế nào? GV đưa h.149 lên bảng và nói: trong một số trường hợp, để việc tính toán thuận lợi, ta có thể chia đa giác thành nhiều tam giác vuông và hình thang vuông. HS quan sát hình vẽ và trả lời câu hỏi. HS: Chia đa giác đó thành nhiều tam giác hoặc các tứ giác đã có công thức tính diện tích, hoặc tạo ra một tam giac nào đó có chứa đa giác=> để tính diện tích của một đa giác bất kì ta quy về tính diện tích các tam giác, các hình thang vuông, hình chữ nhật. E B D C A HS: SABCDE=SABC+SACD+SADE.(T/C diện tích đa giác). HS:SMNPQR=SNST-(SMRS+SPQT) Hoạt động 2 Ví dụ (15’) GV đưa hình 150 lên bảng phụ(kẻ ô vuông) GV: Y/C HS đọc ví dụ tr129 SGK. GV hỏi: Ta có thể chia đa giác đó như thế nào? Gv: Để tính diện tích của các hình này, em cần biết độ dài những đoạn nào? Dùng thước đo độ dài trên hình để biết kết quả? HS đọc ví dụ tr 129 SGK HS: Ta vẽ thêm các đoạn hẳng CG,AH.Vậy đa giác đó được chia thành ba hình: Hình thang vuông CDEG. Hình chữ nhật ABGH. Tam giác AIH HS: Để tính diện tích hình chữ nhật ta cần biết độ dài của AB; AH. Để tính diện tích tam giác cần biết độ dài đường cao IK. HS thực hiện phép đo: CD=2cm; CG=5cm; AH=7cm; DE=3cm; AB=3cm; IK=3cm HS làm vào vở, một HS lên bảng tính. SDEGC==8(cm2) SABGH=3.7=21(cm2); SAIH==10,5(cm2) SABCDEGIH=8+21+10,5=39,5(cm2) HS . để tính diệ tích hình thang vuông càn biết độ dài CD.DE,CG. B A I K E C H G D GV yêu cầu HS tính s các hình, từ đó suy ra diện tích đa giác đã cho? Hoạt động 3 Luyện tập (18’) Bài 38 tr 130 SGK. GV yêu cầu HS hoạt động theo nhóm. Đại diện nhóm trình bày. Bài 40 tr131 SGK. Đề bài và hình ẽ đưa lên bảng phụ. S6 S7 S1 S5 S3 S2 S10 S8 S9 S4 GV: Nêu cách tính diện tích phần gạch sọc trên hình? GV yêu cầu hai HS lên bảng trình bày hai cách khác nhau của S phần gạch sọc. HS hoạt động theo nhóm. Diện tích con đường hình bình hành là: SEBGF=FG.BC=50.120=6 000(m2) Diện tích đám đất hình chữ nhật ABCD là: SABCD=AB.BC=150.120=18 000(m2) Diện tích phần còn lại là: 18 000-6 000=12 000(m2) HS quan sát hình vẽ. HS đọc đề bài,quan sát hình vẽ và tìm cách phân chia hình. Cách 1: Sgạch sọc=S1+S2+S3+S4+S5. Cách 2:Sgạch sọc=SABCD-(S6+S7+S8+S9+S10) Giải: cách 1: S1=(cm2) ; S2=3.5=15(cm2) S3=(cm2); S4=(cm2) S5==>Sgạch sọc= S1+S2+S3+S4+S5. =33,5(cm2) cách 2: Hs Hoạt động 4 Hướng dẫn về nhà (2') Ôn tập chương 2, hình học. Làm 3 câu hỏi ôn tập chương. Bài tập số 37 tr 130, số 39 tr 131, số 42,43 tr132,133 SGK. Tiết 36 A- Mục tiêu HS hiểu và biết vận dụng các công thức vào tính diện tích đa giác. HS tính diện tích hình chữ nhật, hình vuông, hình bình hành, tam giác, hình thoi B- Chuẩn bị của GV và HS Thước kẻ, ê ke, com pa, bút dạ, bảng phụ. C- Tiến trình dạy- học Hoạt động của GV Hoạt động của HS Hoạt động 1 Kiểm tra (8’) GV: Hãy viết các công thức tính diện tích các tứ giác mà em đã học? Viết công thức tính diện tích tam giác đều có cạnh là a? Một HS lên bảng viết. Cả lớp làm vào vở. Hoạt động 2 Luyện tập (35’) Bài 42 tr 132 SGK. (Đề bài và hình vẽ ghi bảng phụ) GV: Nêu cách xác định điểm F? GV: SABCD=S3+S SADF=S3+S SABF=S1+S=1/2BF.? (AH vàCK gọi là gì? Quan hệ như thế nào?) SCBF=S+S=1/2.BF. Từ đó ta suy ra điều gì? SABF=SCBF=>S1=S2=>SABCD=SADF Mở rộng: Cho ngũ giác lồi ABCDE. Hãy vẽ một tam giác có diện tích bằng diện tích ngũ giác đó. Giải thích? A B C D E F G Bài 34 –tr 128 SGK. Cho một hình chữ nhật. Vẽ tứ giác có đỉnh là trung điểm các cạnh của hình chữ nhật. Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật? Từ đó suy ra cách tính diện tích hình thoi? GV: Gọi một HS đọc lại bài ra? Hãy vẽ hình? GV: hãy c/m tứ giác đod là hình thoi? HS vẽ hình vào vở. HS trả lời câu hỏi của GV. Nối AC, từ B vẽ BF//AC(F nằm trên đường thẳng DC). Nối AF. A B H D C F K SABCD=SADC+SABC, Mà SABC=SAFC(vì có đáy AC chung). đường cao BH=FK.=>SABCD=SADC+SAFC hay SABCD=SADF. HS: Nối AC, từ B vẽ đường thẳng //ACkéo dài cắt DC tại F. nối AF. Nối AD, từ E kẻ đường thẳng //AD cắt CD kéo dài tại G. nối AG. Có: SABC=SAFC SAED=SAGDMà SABCDE=SACD+SABC+SAED; SABCDE=SADC+SAFC+SAGD=> SABCDE=SAFG. = = = = A B C D M N P Q HS: Ta có. QM=BD( QM là đường TB của Δ ADB)(1) NP=BD( NP là đường TB của Δ BDC)(2) Từ (1) và (2)=> QM=PN (*) Tưong tự MN=QP; QP= BD(**). Mà BD=AC( t/c đường chéo của HCN) Từ (*) và (**)=>QM=MN=NP=PQ=> MNPQ là hình thoi(đ/n). Shình thoi=MP.QN=AD.AB(3) Shình chữ nhật=AD.AB(4). Từ (3) và (4)=> Shình thoi=Shình chữ nhật. => Cách tính diện tích hình thoi. Từ một đường chéo của hình thoi, ta dựng hình chữ nhật, có một cạnh là đường chéo của hình thoi, cạnh kia bằng đường chéo của hình thoi. Hoạt động 3 Hướng dẫn về nhà (2') Làm bài tập ôn tập chương II- Diện tích đa giác. Viết các công thức tính diện tích của các đa giác đã học. tam giác đồng dạng Tiết 37 A-Mục tiêu Học sinh nắm vững định nghĩa về tỉ số hai đoạn thẳng: +Tỉ số của hai đoạn thẳng là tỉ số đo độ dài của chúng theo cùng một đơn vị đo. + Tỉ số của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo( miễn là khi đo chọn cùng một đơn vị đo) Học sinh nắm vững định nghĩa về đoạn thẳng tỉ lệ. Học sinh cần nắm vững nội dung định lí Ta-Lét( thuận), vận dụng định lí vào việc tìm ra các tỉ số bằng nhau trên hình vẽ trong SGK. B- Đồ dùng dạy- học * Bảng phụ, thước thẳng, thước chia khoảng C-Tiến trình dạy-học Hoạt động của GV Hoạt động của HS Hoạt động 1 ĐặT VấN Đề ( 2’) GV: Tiếp theo chuyên đề về Tam giác, chương này chúng ta sẽ học về tam giác đ.d mà cơ sở của nó là định lí Ta-Lét. Nội dung -Định lí Ta-Lét (thuận,đảo,các hệ quả)-Tính chất đường phân giác của tam giác .-Tam giác đồng dạng và các ứng dụng của nó.Bài đầu tiên của chương là định lí Ta-Lét trong tam giác. HS nghe giáo viên trình bày và xem mục lục trang 134 SGK. Hoạt động 2 1. tỉ số của hai đoạn thẳng (8’) GV: ở lớp 6 ta đã nói đến tỉ số của hai số. Đối với hai đoạn thẳng, ta cũng có khái niệm về tỉ số. Tỉ số của hai đoạn thẳng là gì? GV cho HS làm ?1 tr 56 SGK. Cho AB=3cm; CD=5cm;=? Cho EF =4dm; MN=7dm; =? GV: là tỉ số của hai đ/t AB và CD. Tỉ của hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo( miễn là hai đoạn thẳng phải cùng đơn vị đo). GV: Vậy tỉ số của hai đoạn thẳng là gì? GV giới thiệu kí hiệu tỉ số hai đoạn thẳng. *Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là . GV cho HS đọc ví dụ trang 56 SGK. Bổ sung: AB=60cm; CD=1,5dm. HS cả lớp làm vào vở, một HS lên bảng trình bày: = = HS: Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. AB=300cm CD=400cm AB=3m CD=4m AB=60cm CD=1,5dm=15c Hoạt động 3 2. đoạn thẳng tỉ lệ (7’) GV;Đưa ? 2 lên bảng phụ. Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ So sánh hai tỉ sốVà A B D C B’ A’ D’ C’ Gv Từ tỉ lệ thức= => tỉ lệ thức? GV nêu đ/n(SGK). = hay GV yêu cầu HS đọc lại đ/n tr. 57 SGK = HS làm bài vào vở. Một HS lên bảng làm. = == HS trả lời miệng: = HS đọc lại định nghĩa SGK. Hoạt động 4 3. định lí ta- lét trong tam giác (20’) GV yêu cầu HS làm ? 2 tr 57 SGK , GV đưa hình lên bảng phụ. A B’ C’ a Gv gợi ý:Gọi mỗi đoạn chắn trên cạnh AB là m, mỗi đoạn chắn trên cạnh AC là n. C B GV: Tổng quát. nếu một đ/t // 2 cạnh của Δ thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ. Đó chính là nội dung đ/l Ta Lét. Ta thừa nhận đ/l Ta Lét. GV: Em hãy nhắc lại nội dung của định lí Ta Lét? Viết GT-KL của định lí? GV cho HS đọc ví dụ SGK tr 58. GV cho HS hoạt động theo nhóm ?4 tr 58 SGK. Nửa lớp làm câu a. Nửa lớp làm câu b. HS đọc ? 3 và phần hướng dẫn tr 57 SGK. HS đọc to phần hướng dẫn SGK. HS điền vào bảng phụ HS đọc ví dụ. a//BC A E x C B 5 D 10 a a) x=2 b) y=6,8 Hoạt động 5 Củng cố (5’) GV: Nêu câu hỏi. Nêu đ/n tỉ số 2 đoạn thẳng tỉ lệ và đ/n đoạn thẳng tỉ lệ? Phát biểu định lí Ta Lét trong Δ ? HS trả lời. Hoạt động 6 Hướng dẫn về nhà (3') Học thuộc định lí Ta Lét . bài tập số 1->6 tr 58-59 SGK. A B’ GV hướng dẫn bài số 4. C’ chứng minh rằng. B C a) ; b) Theo GT: =>a) b)
Tài liệu đính kèm:
 hinh hoc 8Tiet 3537.doc
hinh hoc 8Tiet 3537.doc





