Một số bài ôn tập môn Hình học Lớp 8 - Chương: Tứ giác - Phần 1
ĐỀ NGHỊ : Với mỗi bài tập dưới đây, nên vẽ hình lại và kết hợp với HD giải để trình bày hoàn thiện bài làm của mình một cách chặt chẽ và logic. Với mỗi câu chứng minh, nên tìm cách giải khác và trao đổi với bạn về cách giải mới để nắm vững khiến thức tốt hơn !
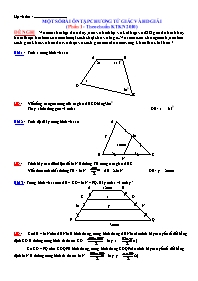
Bài 1 : Tính x trong hình vẽ sau
HD : + Viết tổng các góc trong của tứ giác ABCD bằng 3600
+ Thay số đo từng góc và tính x ĐS : x = 650
Bài 2 : Tính độ dài y trong hình vẽ sau A
HD : + Trình bày các điều kiện để MN là đường TB trong tam giác ABC
+ Viết theo tính chất đường TB : MN = AB = 2.MN ĐS : y = 20cm
Bài 3 : Trong hình vẽ sau có AB // CD // MN // PQ. Hãy tính x và tính y ?
HD : + Có AB // MN nên ABNM là hình thang, trong hình thang ABNM cần trình bày các yếu tố để khẳng định CD là đường trung bình từ đó có CD = hay x = (1)
+ Có CD // PQ nên CDQP là hình thang, trong hình thang CDQP cần trình bày các yếu tố để khẳng định MN là đường trung bình từ đó có MN = hay y = (2)
Họ và tên : ................................. MỘT SỐ BÀI ÔN TẬP CHƯƠNG TỨ GIÁC VÀ HD GIẢI ( Phần 1 - Theo chuẩn KTKN 2010 ) ĐỀ NGHỊ : Với mỗi bài tập dưới đây, nên vẽ hình lại và kết hợp với HD giải để trình bày hoàn thiện bài làm của mình một cách chặt chẽ và logic. Với mỗi câu chứng minh, nên tìm cách giải khác và trao đổi với bạn về cách giải mới để nắm vững khiến thức tốt hơn ! Bài 1 : Tính x trong hình vẽ sau A B 2x 1150 x D 500 C HD : + Viết tổng các góc trong của tứ giác ABCD bằng 3600 + Thay số đo từng góc và tính x ĐS : x = 650 Bài 2 : Tính độ dài y trong hình vẽ sau A y M 10cm B C N HD : + Trình bày các điều kiện để MN là đường TB trong tam giác ABC + Viết theo tính chất đường TB : MN = Þ AB = 2.MN ĐS : y = 20cm Bài 3 : Trong hình vẽ sau có AB // CD // MN // PQ. Hãy tính x và tính y ? A 12cm B C x D M y N P Q 30cm HD : + Có AB // MN nên ABNM là hình thang, trong hình thang ABNM cần trình bày các yếu tố để khẳng định CD là đường trung bình từ đó có CD = hay x = (1) + Có CD // PQ nên CDQP là hình thang, trong hình thang CDQP cần trình bày các yếu tố để khẳng định MN là đường trung bình từ đó có MN = hay y = (2) + Thay x = vào (2) để tìm được y = 24cm + Thay y = 24cm vào (1) để tìm được x = 18cm Bài 4 : Hình thang ABCD ( AB // CD ). Hãy tính x và y ? A B 3x 4y x y D C HD : + Có AB // CD nên hai góc trong cùng phía bù nhau ( có tổng bằng 3600 ) A + D = x + 3x = 1800 + Trình bày tương tự với tính y ĐS : x = 450 và y = 360 Bài 5 : Cho hình thang ABCD (AD//BC).Biết .Tính các góc của hình thang. HD : + Bài này không yêu cầu vẽ hình song nhất thiết phải vẽ nháp để thấy được hướng giải và khi trình bày bài làm không bị sai. + Có AD // BC nên góc A và góc B có tổng bằng 1800 ( trong cùng phía ), kết hợp với Sẽ tính được số đo của mỗi góc ( Bài toán tìm 2 số biết tổng và hiệu ) + Tính được số đo góc A thì dựa vào hệ thức đề cho, ta tính được số đo góc C + Dựa vào quan hệ 2 góc trong cùng phía ( Góc C và D ) ta tính được số đo góc D Bài 6 : Cho tam giác ABC cân tại A. Gọi E,F và D lần lượt là trung điểm của AB, BC, AC. Gọi K là điểm đối xứng với F qua D. Chứng minh: Tứ giác BCDE là hình thang cân. b ) Tứ giác BEDF là hình bình hành c) Tứ giác ADFE là hình thoi d) Tứ giác AFCK là hình chữ nhật HD : + Hình vẽ : A K E D a) B F C + Trong DABC, trình bày các yếu tố để khẳng định ED là đường trung bình, từ đó có ED // BC và Luận BEDC là hình thang. + Hình thang BEDC có hai góc kề cạnh đáy BC bằng nhau ( tam giác ABC cân tại B ) nên là hình Thang cân. b) + Tứ giác BEDF có các cạnh đối song song nên là hình bình hành ( Trình bày các yếu tố để khẳng định ED // BF và BE // DF ) c) + Nêu các yếu tố để khẳng định được DF // AE và EF // AD từ đó có AEFD là hình bình hành + Có AE = và AD = . Vì AB = AC ( tam giác ABC cân tại A ) nên AE = AD. + Hình bình hành AEFD có hai cạnh kề AE và AD bằng nhau nên là hình thoi. d) + Vì K đối xứng với F qua D nên D là trung điểm của KF : FD = DK + Tứ giác AFCK có hai đường chéo cắt nhau tại trung điểm của mỗi đường ( AD = DC, FD = DK ) nên là hình bình hành. + Hình bình hành AFCK có góc AFC bằng 900 ( AF là đường trung tuyến ứng với cạnh đáy của tam giác cân cũng đồng thời là đường cao ) vì thế AFCK là hình chữ nhật. Bài 7 : Cho ABC vuông tại A (AB < AC) , trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA . 1. Tứ giác ABDC là hình gì ? Vì sao ? 2. Gọi I là điểm đối xứng của A qua BC. Chứng minh : BC // ID. 3. Chứng minh : Tứ giác BIDC là hình thang cân. 4. Vẽ HE AB tại E , HF AC tại F. Chứng minh : AM EF. HD : + Hình vẽ : I B D H E M K A C F Tứ giác ABDC có hai đường chéo AD và BC cắt nhau tại trung điểm M của mỗi đường nên là hình bình hành. Hình bình hành ABDC có góc A bằng 900 nên là hình chữ nhật. Tam giác AID có HM là đường trung bình nên HM // ID hay ID // BC A và I đối xứng qua BC nên BC là đường trung trực của AI vậy CI = CA, mà CA = BD nên IC = DB. Tứ giác BIDC có ID // BC và IC = BD nên là hình thang cân. Gọi K là giao điểm của EF và AM. Tam giác MBA cân tại M nên góc MBA bằng góc MAB. Có AEHF là hình chữ nhật nên góc FEA bằng góc HAB. Có tổng hai góc HAB và góc MBA bằng 900 nên tổng hai góc FEA và góc MAB bằng 900 . Tam giác AEK có tổng hai góc FEA và góc MAB bằng 900 nên vuông tại K. Vậy EF ^ AM tại K Bài 8 : Cho tam giác ABC vuông ở C. GọI M, N lần lượt là trung điểm của các cạnh BC và AB. GọI P là điểm đốI xứng của M qua điểm N Chứng minh tứ giác MBPA là hình bình hành. Chứng minh tứ giác PACM là hình chữ nhật. Đường thẳng CN cắt PB ở Q. Chứng minh : BQ = 2PQ Tam giác ABC cần có thêm điều kiện gì thì hình chữ nhật PACM là hình vuông ? Hãy chứng minh ? Gợi ý câu c : Từ M hãy kẻ đường thẳng song song với CQ và cắt QB tại E, c/m BE = EQ = QP để rút ra điều cần c/m ! Gợi ý câu d : Hình chữ nhật PACM là hình vuông khi có thêm AC = CM mà CM = nên AB = . Vậy tam giác vuông ABC đồng thời là nửa tam giác đều thì PACM là hình vuông.
Tài liệu đính kèm:
 mot_so_bai_on_tap_mon_hinh_hoc_lo_8_chuong_tu_giac.doc
mot_so_bai_on_tap_mon_hinh_hoc_lo_8_chuong_tu_giac.doc





