Giáo án tự chọn môn Toán Lớp 9 - Năm học 2009-2010

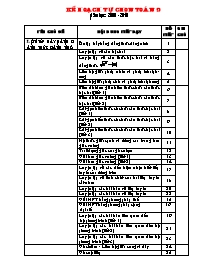
Kế hoạch tự chọn toán 9
Năm học: 2009 - 2010
Tên chủ đề
Nội dung tiết dạy
Số tiết
Ghi chú
I. ôn tập bảy hằng đẳng thức đáng nhớ
Ôn tập bảy hằng đẳng thức đáng nhớ
1
Luyện tập về căn bậc hai
2
Luyện tập về căn thức bậc hai và hằng đẳng thức 
3
Liên hệ giữa phép nhân và phép khai phơng
4
Liên hệ giữa phép chia và phép khai phơng
5
Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiết 1)
6
Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiết 2)
7
Rút gọn biểu thức có chứa căn thức bậc hai (tiết 1)
8
Rút gọn biểu thức có chứa căn thức bậc hai (tiết 2)
9
Rút gọn biểu thức có chứa căn thức bậc hai (tiết 3)
10
Hệ thức giữa cạnh và đờng cao trong tam giác vuông
11
Tỉ số lợng giác của góc nhọn
12
Giải tam giác vuông (tiết 1)
13
Giải tam giác vuông (tiết 2)
14
Luyện tập về các dấu hiệu nhận biết tiếp tuyến của đờng tròn
17
Luyện tập về tính chất của hai tiếp tuyến cắt nhau
18
Luyện tập các bài toán về tiếp tuyến 
20
Luyện tập các bài toán về tiếp tuyến
22
Giải HPT bằng phơng pháp thế
15
Giải HPT bằng phơng pháp cộng
 đại số
 16
Luyện tập các bài toán liên quan đến
 hệ phơng trình (tiết 1)
19
Luyện tập các bài toán liên quan đến hệ phơng trình (tiết 2)
21
Luyện tập các bài toán liên quan đến hệ phơng trình (tiết 3)
23
Góc ở tâm - Liên hệ giữa cung và dây
24
Góc nội tiếp
25
Góc tạo bởi tia tiếp tuyến và dây cung
26
Luyện tập về giải phơng trình bậc hai.
27
Luyện tập các bài toán liên quan đến phơng trình bậc hai.
30
Luyện tập các bài toán liên quan đến phơng trình bậc hai (tiếp)
31
Luyện tập các bài toán liên quan đến phơng trình bậc hai (tiếp)
33
Luyện tập các bài toán về tứ giác nội tiếp
28
Luyện tập các bài toán về tứ giác nội tiếp (tiếp)
29
Luyện tập các bài toán liên quan đến tứ giác nội tiếp (tiếp)
32
Luyện tập về hệ thức Vi-ét
34
Luyện tập về hệ thức Vi-ét (tiếp)
35
Hồng Hng, ngày 04 tháng 09 năm 2009
Ngày soạn : 04/09/09
Ngày dạy : 12/09/09
Chủ đề 1
Tiết 1
ôn tập bảy hằng đẳng thức đáng nhớ
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
Củng cố lại cho HS 7 hằng đẳng thức đáng nhớ, từ đó áp dụng vào biến đổi; khai triển bài toán về hằng đẳng thức cũng nh bài toán ngợc của nó .
Kĩ năng 
Qua các bài tập rèn luyện kỹ năng biến đổi biểu thức, áp dụng 7 hằng đẳng thức.
Thái độ 
Có ý thức tự giác học tập. 	
B/Chuẩn bị của thầy và trò
- GV: 
- HS:
Ôn tập lại bảy hằng đẳng thức đáng nhớ
C/Tiến trình bài dạy
I. Kiểm tra bài cũ (7 phút)	
- HS1: 
Nêu lại 7 hằng đẳng thức đã học.
Tính : ( x - 2y )2 
- HS2:
Tính ( 1 - 2x)3 
II. Bài mới (32 phút)
Hoạt động của GV và HS
Nội dung
1.	Ôn tập lí thuyết (5 phút)
- GV gọi HS phát biểu bằng lời 7 hằng đẳng thức đã học 
- GV yêu cầu HS ghi nhớ lại . 
- Bảy hằng đẳng thức đáng nhớ đợc giữ nguyên trên bảng
2.	Luyện tập ( 27 phút)
- GV ra bài tập 11 , 12 ( SBT ) gọi HS đọc đề bài và yêu cầu nêu hằng đẳng thức cần áp dụng . 
- Để tính các biểu thức trên ta áp dụng hằng đẳng thức nào ? nêu cách làm ? 
- HS lên bảng làm bài , GV kiểm tra và sửa chữa . 
- GV ra bài tập gọi HS đọc đề bài , nêu cách làm .
- Bài toán trên cho ở dạng nào ? ta phải biến đổi về dạng nào ? 
- Gợi ý : Viết tách theo đúng công thức rồi đa về hằng đẳng thức 
 - GV ra bài tập gọi HS đọc đề bài sau đó HD học sinh làm bài tập . 
- Hãy dùng hằng đẳng thức biến đổi sau đó thay giá trị của biến vào biểu thức cuối để tính giá trị của biểu thức . 
- GV cho HS làm sau đó gọi HS lên bảng trình bày lời giải , GV chữa bài và chốt lại cách giải bài toán tính giá trị biểu thức . 
- GV ra bài tập gọi HS đọc đề bài sau đó HD học sinh làm bài tập . 
- Muốn chứng minh hằng đẳng thức ta phải làm thế nào ? 
- Gợi ý : Hãy dùng HĐT biến đổi VT thành VP từ đó suy ra điều cần chứng minh . 
- GV gọi HS lên bảng làm mẫu sau đó chữa bài và nêu lại cách chứng minh cho HS . 
*) Bài 11 ( SBT - 4 ) 
a)	( x + 2y )2 = (x)2 + 2.x.2y + (2y)2 
= x2 + 4 xy + 4y2 .
b)	( x- 3y )(x + 3y) = x2 - (3y)2 = x2 - 9y2 .
c)	(5 - x)2 = 52 - 2.5.x + x2 
= 25 - 10 x + x2 .
*) Bài 12d,13 ( SBT - 4 ) 
d)	( = 
a)	x2 + 6x + 9 = x2 +2.3.x + 32 = (x + 3)2 
b)	
c)	2xy2 + x2y4 +1 = (xy2)2 + 2.xy2.1+1
 = (xy2 + 1)2
*) Bài 16 ( SBT - 5 ) 
a)	Ta có : x2 - y2 = ( x + y )( x - y ) (*) 
Với x = 87 ; y = 13 thay vào (*) ta có :
 x2 - y2 = ( 87 + 13)( 87 - 13) = 100 . 74 
 = 7400 
b)	Ta có : x3 - 3x2 + 3x - 1 = ( x- 1 )3 (**) 
Thay x = 101 vào (**) ta có : 
(x - 1)3 = ( 101 - 1)3 = 1003 = 1000 000 .
c)	Ta có : x3 + 9x2 + 27x + 27 
= x3 + 3.x2.3 + 3.x.32 + 33 
= ( x + 3)3 (***)
Thay x = 97 vào (***) ta có :
(x+3 )3 = ( 97 + 3 )3 = 1003 
 = 1000 000 000 .
*) Bài 17 ( SBT - 5 ) 
a)	Ta có : 
VT = ( a + b )( a2 - ab + b2 )+ ( a- b)( a2 + ab + b2)
= a3 + b3 + a3 - b3 = 2a3 
- Vậy VT = VP ( Đpcm ) 
b)	Ta có : 
VT= ( a2 + b2)( c2 + d2) 
 = a2c2 + a2d2 + b2c2 + b2d2 
= ( ac)2 + 2 abcd + (bd)2 + (ad)2 - 2abcd +(bc)2 
 = ( ac + bd)2 + ( ad - bc)2 
- Vậy VT = VP ( Đpcm )
III. Củng cố (5 phút)
- Nhắc lại 7 HĐT đã học ?
- Nêu cách chứng minh đẳng thức 
*) Giải bài tập 18 ( SBT - 5 )
 Gợi ý : Viết x2 - 6x + 10
 = x2 - 2.x.3 + 9 + 1 
 = ( x - 3)2 + 1 
IV. Hớng dẫn về nhà (1 phút)
Học thuộc các HĐT, giải bài tập 18( b) , BT 19 ( 5 ) ; BT 20 ( 5 ) 
Ngày soạn : 11/09/09
Ngày dạy : 19/09/09
Chủ đề 2
Tiết 2
Luyện tập về căn bậc hai
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
- Củng cố cho học sinh về định nghĩa CBHSH, định lí a <b ú .	
Kĩ năng 
- Rèn kĩ năng tìm CBH, CBHSH của một số, kĩ năng so sánh hai căn bậc hai, bài toán tìm x
Thái độ 
- ý thức ham học hỏi, rèn tính cẩn thận.
B/Chuẩn bị của thầy và trò
- GV: 
- HS:
C/Tiến trình bài dạy
I. Kiểm tra bài cũ (7 phút)	
- HS1: 
Nêu định nghĩa CBHSH của một số không âm ?
Tìm CBHSH của: 16; 37; 36; 49; 81 ?
- HS2:
Tìm CBH của: 16; 37; 36; 49; 81 ? 
II. Bài mới (35 phút)
Hoạt động của GV và HS
Nội dung
1.	Lí thuyết (5 phút)
- GV cho học sinh nhắc lại về lí thuyết 
+ Định nghĩa CBHSH ?
+ Định lí về so sánh hai CBH ?
*) 
*) Với hai số a; b không âm ta có:
2.	Tìm căn bậc hai số học, căn bậc hai
của một số không âm ( 10 phút)
- GV tổ chức cho học sinh thi giải toán nhanh ?
- GV cho các đội nhận xét chéo 
a) Tìm CBHSH của:
0,01; 0,04; 0,81; 0,25.
b) Tìm căn bậc hai của:
16; 121; 37; 5
3.	So sánh ( 10 phút)
- Tổ chức cho học sinh thảo luận nhóm ?
- Đại diện từng nhóm lên giải thích bài làm của nhóm mình ?
- Các nhóm nhận xét và cho điểm?
a) 2 và .
Ta thấy: 2 =1+1
mà 1 < Vậy 2 < 
b) 1 và 
Ta thấy 1=2-1
mà 2= nên 1 >
c) và 10
Ta thấy 10=2.5=2.
4. Tìm x (10 phút)
- Nêu phơng pháp làm dạng toán này ?
- HD: đa vế phải về dạng căn bậc hai.
+ Vận dụng định lí để tìm.
- GV cho học sinh thảo luận theo nhóm khoảng phút
- Đại diện các nhóm lên trình bày?
- GV nhấn mạnh phơng pháp làm.
a) 
Vì 3 =
nên ú x=9
b) 
ú ú x=81
III. Củng cố (2 phút)
- Nêu lại các phơng pháp làm các dạng toán đã nêu ở trên ?
- GV lu ý kĩ dạng toán tìm x.
IV. Hớng dẫn về nhà (1 phút)
	- Học lại các định nghĩa, định lí.
	- Xem lại các dạng bài tập đã chữa.
	- Làm trớc các bài tập phần căn thức bậc hai
*******************************
Ngày soạn : 18/09/09
Ngày dạy : 26/09/09
Chủ đề 2
Tiết 3
Luyện tập về căn thức bậc hai 
và hằng đẳng thức 
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
	- Củng cố lại cho học sinh các khái niệm về căn thác bậc hai , định nghĩa , kí hiệu và cách khai phơng căn bậc hai một số .
ỉ	Kĩ năng 
	- Kĩ năng áp dụng hằng đẳng thức vào bài toán khai phơng và rút gọn biểu thức có chứa căn bậc hai đơn giản . Cách tìm điều kiện để căn thức có nghĩa . 
Thái độ 
- Học sinh tự giác, tích cực, say mê học tập	
B/Chuẩn bị của thầy và trò
- GV: 
- HS:
C/Tiến trình bài dạy
I. Kiểm tra bài cũ (3 phút)	
- HS1: 
Nêu điều kiện xác định của , 
Hằng đẳng thức , lấy ví dụ minh hoạ . 
- HS2:
Tìm điều kiện xác định của 
II. Bài mới (34 phút)
Hoạt động của GV và HS
Nội dung
1.	Lí thuyết ( 4 phút)
- Nêu điều kiện để căn thức có nghĩa ? 
- Nêu hằng đẳng thức căn bậc hai đã học . 
*) Để có nghĩa thì A ³ 0 . 
*) Với A là biểu thức ta luôn có : 
2. Luyện tập ( 30 phút)
- GV ra bài tập 9 yêu cầu HS chứng minh định lý . 
- nếu a 0 ta suy ra và a - b ? 
- Gợi ý : Xét a - b và đa về dạng hiệu hai bình phơng . 
- Kết hợp (1) và (2) ta có điều gì ? 
- Hãy chứng minh theo chiều ngợc lại . HS chứng minh tơng tự . ( GV cho HS về nhà ) .
- GV ra tiếp bài tập cho HS làm sau đó gọi HS lên bảng chữa bài . - GV sửa bài và chốt lại cách làm .
- Nêu điều kiện để căn thức có nghĩa .
- GV ra tiếp bài tập 14 ( SBT /5 )
- Gọi HS nêu cách làm và làm bài
- Gợi ý : đa ra ngoài dấu căn có chú ý đến dấu giá trị tuyệt đối . 
- GV nhấn mạnh.
- GV ra bài tập 15 ( SBT / 5 ) hớng dẫn học sinh làm bài . 
- Hãy biến đổi VT thành VP để chứng minh đẳng thức trên . 
- Gợi ý : Chú ý áp dụng 7 hằng đẳng thức đáng nhớ vào căn thức . 
- GV gợi ý HS biến đổi về dạng bình phơng để áp dụng hằng đẳng thức để khai phơng 
- Gọi HS lên bảng trình bày lời giải . 
*) Bài tập 9a ( SBT / 4 ) . 
- Ta có a < b , và a , b ³ 0 ta suy ra : 
- Lại có a < b đ a - b < 0 
đ 
- Từ (1) và (2) ta suy ra
- Vậy chứng tỏ : a < b đ 
 ( đpcm)
*) Bài tập 12 ( SBT / 5 ) 
a) Để căn thức trên có nghĩa ta phải có 
- 2x + 3 ³ 0 đ - 2x ³ -3 đ x Ê .
Vậy với x Ê thì căn thức trên có nghĩa 
c) để căn thức có nghĩa ta phải có 
x + 3 > 0 đ x > - 3 .
Vậy với x > - 3 thì căn thức trên có nghĩa . 
*) Bài tập 14 ( SBT / 5 ) Rút gọn biểu thức .
a) 
b)
c) ( vì )
d) 
( vì ) 
*) Bài tập 15 ( SBT / 5 ) 
a) 
- Ta có : 
VT=
 = . 
- Vậy đẳng thức đã đợc chứng minh . 
d) 
Ta có : 
VT =
 = 
- Vậy VT = VP ( đpcm)
III. Củng cố (7 phút)
-Nêu lại định nghĩa căn bậc hai số học và điều kiện để căn thức có nghĩa . 
- áp dụng lời giải các bài tập trên, hãy giải bài tập 13a,d ( SBT/5 ) 
- Giải bài tập 21 ( a )/SBT (6) . 
*) Bài tập 13a,d ( SBT / 5 ) 
a) 20	d) 298
*) Bài tập 21a ( SBT / 6 ) 
- Biến đổi 
- Rút gọn đợc kết quả là - 1
IV. Hớng dẫn về nhà (1 phút)
	-Xem lại các bài tập đã giải , học thuộc định nghĩa , hằng đẳng thức và cách áp dụng .
Giải tiếp các phần còn lại của các bài tập đã làm . 
	- áp dụng tơng tự giải bài tập 19 , 20 , 21 ( SBT / 6 ) 
*******************************
Ngày soạn : 25/09/09
Ngày dạy : 03/10/09
Chủ đề 2
Tiết 4
Liên hệ giữa phép nhân và phép khai phơng
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
- Củng cố lại cho học sinh quy tắc khai phơng một tích và nhân các căn thức bậc hai . 
- Nắm chắc đợc các quy tắc và vận dụng thành thạo vào các bài tập để khai phơng mộ ...  xét chữa bài và chốt cách chứng minh . 
*) Giải bài tập 39 ( SBT - 79 ) 
Xét tứ giác EHCD có : 
( góc có đỉnh bên trong đờng tròn ) ( 1) 
 ( góc nội tiếp chắn cung SC ) ( 2)
Theo ( gt ) ta có : ( 3) 
Từ (1) ; (2) ; (3) suy ra :
Vậy tứ giác EHCD có tổng hai góc đối diện nhau bằng 1800 đ tứ giác EHCD nội tiếp .
*) Bài tập 40 ( SBT - 40 ) 
GT : Cho D ABC ; BS , CS là phân giác trong ; BE , CE là phân giác ngoài 
KL : Tứ giác BSCE là tứ giác nội tiếp .
Chứng minh :
Theo ( gt) ta có BS là phân giác trong của góc B 
đ ( 1) 
BE là phân giác ngoài của 
đ ( 2) 
Mà (3)
Từ (1) ; (2) và (3) suy ra :
đ (*) 
- Chứng minh tơng tự với CS và CE là phân giác trong và phân giác ngoài của 
góc C ta cũng có : 
đ (**) 
Từ (*) và (**) suy ra tứ giác BSCE là tứ giác nội tiếp . 
IV. Củng cố (7 phút)
 - Nêu lại tính chất của tứ giác nội tiếp . 	
- Vẽ hình ghi GT , Kl bài tập 42 ( SBT - 79 ) 
GT : Cho (O1) ầ (O2) ầ (O3) º P (O1) ầ (O2) º B ; (O1) ầ (O3) º A ; (O2) ầ (O3) º C DB ầ (O1) º M ; DC ầ (O3) º N 
KL : Chứng minh M , A , N thẳng hàng 
V. Hớng dẫn về nhà (2 phút)
Học thuộc định nghĩa , định lý . 
Xem lại các bài tập đã chữa . 
Giải bài tập 42 ( SBT - 79 ) 
HD : Tính = 1800 
+ Xét các tứ giác nội tiếp : MAPB ; NAPC và DBPC dùng tổng các góc đối trong tứ giác nội tiếp bằng 1800 từ đó suy ra góc MAN bằng 1800 . 
*******************************
*) Hãy giữ phím ctrl và nhấn vào đờng link này - 
Ngày soạn : 02/04/10
Ngày dạy : 10/04/10
Chủ đề IX
tứ giác nội tiếp
Tiết 29
Luyện tập các bài toán về tứ giác nội tiếp (tiếp)
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
- Tiếp tục củng cố cho HS khái niệm về tứ giác nội tiếp một đờng tròn, nắm đợc định lý về tứ giác nội tiếp .
- Biết vận dụng định nghĩa, định lý để chứng minh một tứ giác nội tiếp .
Kĩ năng 
- Rèn kỹ năng chứng minh tứ giác nội tiếp và vận dụng tứ giác nội tiếp để chứng minh bài toán hình liên quan. 
Thái độ 
- Có thái độ học tập đúng đắn, tinh thần hoạt động tập thể.
B/Chuẩn bị của thầy và trò
- GV: 
Thớc, compa, thớc đo độ
- HS:
Thớc, compa, thớc đo độ
C/Tiến trình bài dạy
I. Tổ chức (1 phút) 
II. Kiểm tra bài cũ (thông qua bài giảng)
III. Bài mới (35 phút)
Hoạt động của GV và HS
Nội dung
1. Bài tập 41 (SBT/79) (phút)
- GV ra bài tập 41 ( SBT - 79), gọi HS đọc đầu bài sau đó vẽ hình vào vở . 
- Bài toán cho gì ? yêu cầu chứng minh gì ? 
- Để chứng minh tứ giác ABCD nội tiếp đ ta cần chứng minh gì ? 
- GV cho HS thảo luận nhóm đa ra cách chứng minh . 
- GV gọi 1 nhóm đại diện chứng minh trên bảng, các nhóm khác theo dõi nhận xét và bổ sung lời chứng minh . 
- Gợi ý : Dựa theo gt tính các góc : sau đó suy ra từ định lý . 
- Tứ giác ABCD nội tiếp đ góc AED là góc gì có số đo tính theo cung bị chắn nh thế nào ? 
- Hãy tính số đo góc AED theo số đo cung AD và cung BC rồi so sánh với hai góc DBA và góc BAC ? 
- GV cho HS làm sau đó gọi 1 HS lên bảng tính . 
GT : D ABC ( AB = AC ) 
 ; DA = DB ; 
KL :
a) Tứ giác ACBD nội tiếp 
b) Tính góc AED.
 Chứng minh : 
a) Theo (gt) ta có D ABC cân tại A 
lại có đ 
Theo ( gt) có DA = DB đ D DAB cân tại D đ 
Xét tứ giác ACBD có : 
 = 400 + 200 + 400 +800 = 1800 
Vậy theo định lý về tứ giác nội tiếp đ tứ giác ACBD nội tiếp 
b) Vì tứ giác ACBD nội tiếp đ ta có : 
( góc có đỉnh bên trong đờng tròn ) 
đ ( góc nội tiếp chắn cung AD và BC ) 
đ 
Vậy góc AED bằng 600 . 
2. Bài tập 43 (SBT/79) ( phút)
- GV ra tiếp bài tập 43 - SBT, vẽ hình minh hoạ trên bảng yêu cầu HS thảo luận tìm cách chứng minh bài toán ? 
? Nếu hai điểm cùng nhìn một cạch cố định dới những góc bằng nhau thì 4 điểm đó thoả mãn điều kiện gì ? áp dụng tính chất nào ? 
- Vậy theo em bài toán trên nên chứng minh nh thế nào ? 
- Gợi ý : 
+ Chứng minh D AEB đồng dạng với D DEC sau đó suy ra cặp góc tơng ứng bằng nhau ? 
+ Dùng quỹ tích cung chứa góc chứng minh 4 điểm A , B , C , D cùng thuộc một đờng tròn . 
- GV cho HS chứng minh sau đó lên bảng trình bày lời chứng minh . GV nhận xét và chữa bài chốt cách làm . 
GT : AC BD = 
 AE.EC = BE.ED 
KL : Tứ giác ABCD 
 nội tiếp . 
Chứng minh : 
Theo ( gt ) ta có : AE . EC = BE . ED suy ra ta có : 
 (1) 
Lại có : ( đối đỉnh ) (2)
Từ (1) và (2) suy ra : 
D AEB đồng dạng với D DEC 
đ ( hai góc tơng ứng ) 
Đoạn thẳng BC cố định , ( cmt ) ; A và D ở trong cùng một nửa mặt phẳng bờ là BC nên 4 điểm A , B , C , D cùng nằm trên một đờng tròn 
( theo quỹ tích cung chứa góc ) 
IV. Củng cố (7 phút)
- Nêu lại tính chất của tứ giác nội tiếp . 	
	- Nhắc lại một số cách chứng minh tứ giác nội tiếp.
*) Bài tập củng cố: Quan sát hình vẽ và điền vào dấu “...” hoàn thành các khẳng định sau cho đúng . 
1. Góc ở tâm là góc . . . . . . có số đo bằng số đo của cung AD . 
2. Góc nội tiếp là các góc . . . . . . . . . . . . . . . . . . . .
3. Góc AED là góc . . . . . . . . . . . . . . . . . . . . . . . có số đo 
bằng . . . . số đo của cung . . . . . . . và cung . . . . . . . 
4. Góc ACD có số đo bằng nửa số đo của góc . . . . . . . . . . . 
V. Hớng dẫn về nhà (2 phút)
- Làm tiếp các bài tập và ôn luyện lại lí thuyết.
* Bài tập về nhà: Cho D ABC ( AB = AC ) nội tiếp trong đờng tròn (O) . Các đờng cao AG, BE, CF cắt nhau tại H .
a) Chứng minh tứ giác AEHF nội tiếp. Xác định tâm I của đờng tròn ngoại tiếp tứ giác đó . 
b) Chứng minh : AF . AC = AH . AG 
c) Chứng minh GE là tiếp tuyến của (I) . 
Ngày soạn : 03/05/10
Ngày dạy : /05/10
Chủ đề IX
tứ giác nội tiếp
Tiết 32
Luyện tập các bài toán về tứ giác nội tiếp (tiếp)
A/Mục tiêu
Học xong tiết này HS cần phải đạt đợc :
Kiến thức 
- Củng cố, ôn tập lại cho học sinh các kiến thức về góc với đờng tròn, tứ giác nội tiếp .	
Kĩ năng 
- Rèn kỹ năng vận dụng các kiến thức đã học trong chuyên đề để làm một số bài toán tổng hợp về đờng tròn .
Thái độ 
- Có thái độ học tập đúng đắn.	
B/Chuẩn bị của thầy và trò
- GV: 
Bảng phụ, thớc, compa, êke
- HS:
Thớc, compa, êke
C/Tiến trình bài dạy
I. Tổ chức (1 phút)	
II. Kiểm tra bài cũ (7 phút)	
- HS1: 
Nêu các góc có liên quan với đờng tròn đã học ?
Phát biểu các định lý, tính chất giữa góc và đờng tròn ?
- HS2:
Nêu các dấu hiệu nhận biết tứ giác nội tiếp ?
III. Bài mới (27 phút)
Hoạt động của GV và HS
Nội dung
1. Bài tập 73 (SBT/84) (12 phút)
- GV ra bài tập 73 ( SBT - 84 ) yêu cầu học sinh đọc đề bài , vẽ hình và ghi GT , KL của bài toán .
- Bài toán cho gì ? yêu cầu gì ? 
- Thảo luận và đa ra cách chứng minh các hệ thức trên . 
- Để chứng minh các hệ thức trên ta thờng đi chứng minh gì ? ( tam giác đồng dạng ) 
- Theo em nên chứng minh những tam giác nào đồng dạng ? 
- GV cho HS suy nghĩ và nêu cách làm . 
- GV gợi ý : Chứng minh D AA’B đồng dạng với D BAB’ ( g.g ) 
- HS làm sau đó lên bảng trình bày - GV nhận xét và chữa bài . 
- Tơng tự đối với hệ thức ở phần (b) ta nên chứng minh các cặp tam giác nào đồng dạng . 
- HS nêu GV nhận xét và gợi ý lại : Chứng minh D A’MA đồng dạng với D A’AB .
- Cách khác : áp dụng hệ thức lợng trong tam giác vuông ABA’
GT : Cho (O ; ) 
 Ax , By là hai tiếp tuyến của (O) 
 M ẻ (O) ; 
KL : a) AA’ . BB’ = AB2 
 b) A’A2 = A’M . A’B 
Chứng minh 
a) Ta có (góc nội tiếp chắn nửa đờng tròn)
Xét D AA’B và D BAB’ có 
( vì Ax và By là tiếp tuyến ) 
 ( cùng phụ với góc BAB’ ) 
đ D AA’B đồng dạng với D BAB’ ( g.g ) 
đ ( Đcpcm ) 
b) Xét D A’MA và D A’AB có . 
 ( chung ) 
đ D A’MA đồng dạng với D A’AB 
đ (Đcpcm ) 
2. Chữa bài về nhà ( 15 phút)
Đề bài: Cho D ABC ( AB = AC ) nội tiếp trong đờng tròn (O). Các đờng cao AG , BE , CF cắt nhau tại H 
a) Chứng minh tứ giác AEHF nội tiếp . Xác định tâm I của đờng tròn ngoại tiếp tứ giác đó . 
b) Chứng minh : AF . AC = AH . AG 
c) Chứng minh GE là tiếp tuyến của (I)
- GV treo bảng phụ ghi đầu bài bài tập về nhà, yêu cầu HS đọc đề bài , vẽ hình và ghi GT , KL của bài toán . 
- Bài toán cho gì ? yêu cầu gì ? 
- Theo em để chứng minh tứ giác AEHF là tứ giác nội tiếp 
đ ta cần chứng minh gì ? 
- Hãy chứng minh tứ giác có 2 góc vuông đối diện nhau ? 
- HS chứng minh miệng , GV chốt lại vấn đề . 
- Có nhận xét gì về điểm E và F của tứ giác AEHF ? Vậy E , F nằm trên đờng tròn nào ? Tâm ở đâu ? 
- Để chứng minh hệ thức trên ta chứng minh gì ? 
- Hãy chứng minh D AFH đồng dạng với D AGB ?
- HS chứng minh .
- Để chứng minh GE là tiếp tuyến của (I) ta cần chứng minh gì ? 
- Gợi ý : Chứng minh GE ^ IE tại E . 
- HS suy nghĩ chứng minh bài . 
- Gợi ý : Xét D cân IAE , D cân GBE và tam giác vuông HEA . 
- HS lên bảng trình bày , GV chữa bài và chốt cách làm
Chứng minh 
 a) Theo ( gt ) ta có : 
AG , BE , CF là 3 đờng cao của tam giác cắt nhau tại H 
đ 
đ Tứ giác AEHF có tổng hai góc đối diện bằng 1800 
=> Tứ giác AEHF là tứ giác nội tiếp . 
Vì E , F nhìn AH dới một góc bằng 900 đ Theo quỹ tích cung chứa góc E , F nằm trên đờng tròn đờng kính AH 
đ tâm I của đờng tròn ngoại tiếp tứ giác EHFF là trung điểm của AH . 
b) Xét D AFH và D AGB có : 
đ D AFH đồng dạng với D AGB 
đ (*) 
Lại có AB = AC ( gt) đ Thay vào (*) ta có AF . AC = AH . AG ( Đcpcm ) 
c) Xét D IAE có IA = IE (vì I là tâm đờng tròn ngoại tiếp tứ giác AEHF ) 
đ D IAE cân đ 
Xét D CBE có EG là trung tuyến ( Do AG là đờng cao của D ABC cân đ BG = GC ) 
đ GE = GB = GC đ D GBE cân tại G 
đ 
Lại có 
đ ( 3) 
Mà 
Từ (1) , (2) , (3) và (4) => GE ^ IE 
=> GE là tiếp tuyến của (I) tại E . 
IV. Củng cố (7 phút)
- Nêu các góc liên quan tới đờng tròn mà em đã học . 
- Nêu tính chất của các góc liên quan tới đờng tròn . 
- Khi nào một tứ giác nội tiếp trong một đờng tròn . 
*) Bài tập: Đánh dấu “X” vào cột đúng ( Đ ) hoặc sai ( S) em cho là đúng 
Câu
Nội dung
Đ
S
1
Hai góc nội tiếp bằng nhau thì phải cùng chắn một cung
x
2
Góc ở tâm có số đo bằng nửa số đo của góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung
x
3
Góc có đỉnh ở ngoài đờng tròn có số đo bằng tổng số đo của hai cung bị chắn
x
4
Tứ giác có tổng hai góc đối bằng 1800 thì tứ giác đó nội tiếp đợc trong một đờng tròn
x
V. Hớng dẫn về nhà (3 phút)
Ôn lại các kiến thức đã học, nắm chắc các định nghĩa và tính chất . 
Học thuộc các định lý và vận dụng vào chứng minh bài toán liên quan 
Xem lại các bài đã chữa và làm các bài tập còn lại trong SBT , SGK phần góc với đờng tròn , tứ giác nội tiếp .
Tiết sau học : “Luyện tập các bài toán liên quan đến phơng trình bậc hai (tiếp)” 
	*) Bài tập về nhà: 
Cho tam giác vuông ABC ( ), đờng cao AH .
Vẽ đờng tròn đờng kính HB và HC cắt các cạnh AB và AC lần lợt tại
E và F 
a) Chứng minh tứ giác AEHF là hình chữ nhật . 
b) Chứng minh tứ giác BEFC là tứ giác nội tiếp . 
*******************************
*) Hãy giữ phím ctrl và nhấn vào đờng link này -