Giáo án môn Hình học Lớp 8 - Tiết 24: Kiểm tra chương I - Năm học 2011-2012 - Nguyễn Huy Du
1/Mục đích của đề kiểm tra:
Thu thập thông tin để đánh giá xem học sinh có đạt được chuẩn kiến thức kĩ năng trong chương trình hay không, từ đó điều chỉnh PPDH và đề ra các giải pháp thực hiện cho các kiến thức tiếp theo.
2/ Hình thức đề kiểm tra :
Tự luận với nhiều bài tập nhỏ.
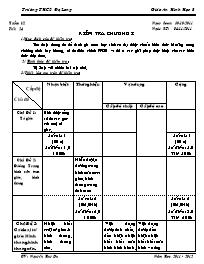
3/ Thiết lập ma trận đề kiểm tra:
Bạn đang xem tài liệu "Giáo án môn Hình học Lớp 8 - Tiết 24: Kiểm tra chương I - Năm học 2011-2012 - Nguyễn Huy Du", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày Soạn: 30/10/2011 Ngày KT: 04/11/2011 Tuần: 12 Tiết: 24 KIỂM TRA CHƯƠNG I 1/Mục đích của đề kiểm tra: Thu thập thông tin để đánh giá xem học sinh có đạt được chuẩn kiến thức kĩ năng trong chương trình hay không, từ đó điều chỉnh PPDH và đề ra các giải pháp thực hiện cho các kiến thức tiếp theo. 2/ Hình thức đề kiểm tra : Tự luận với nhiều bài tập nhỏ. 3/ Thiết lập ma trận đề kiểm tra: Cấp độ Chủ đề Nhận biết Thông hiểu Vận dụng Cộng Cấp độ thấp Cấp độ cao Chủ Đề 1: Tứ giác Biết được tổng số đo các góc của một tứ giác. Số câu: 1 (B1a) Số điểm: 1,0 100% Số câu: 1 (B1a) Số điểm: 1,0 Tỉ lệ 10% Chủ Đề 2: Đường Trung bình của tam giác, hình thang Hiểu đựợc đường trung bình của tam giác, hình thang trong tính toán Số câu: 2 (B2,B4b) Số điểm: 2,0 100% Số câu: 2 (B2, B4b) Số điểm: 2,0 Tỉ lệ 20% Chủ Đề 3: Các loại tứ giác: Hình thang, hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuông Nhận biết một tứ giác là hình thang, hình thang cân. Vận dụng dược tính chất, dấu hiệu nhận biết biết của hình bình hành, hình chữ nhật, hình thoi, định lí pytago để tính cạnh của hình thoi, chứng minh tứ giác là hình bình hành Vận dụng dược dấu hiệu nhận biết biết của hình vuông để tìm điều kiện của tứ giác để hình bình hành trở thành hình vuông. Số câu: 2 (B1b,B4a) Số điểm: 2,0 30% Số câu: 2 (B3,B5a) Số điểm: 4,0 55% Số câu: 1 (B5b) Số điểm: 1,0 15% Số câu: 5 (B1b,B4a, B3,B5a,b) Số điểm: 7,0 Tỉ lệ 70% 5 bài số câu: 9 Tổng số điểm 10,0 Tỉ lệ : 100% Số câu: 3 Số điểm: 3,0 30 % Số câu:2 Số điểm: 2,0 20 % Số câu: 2 Số điểm: 4,0 40 % Số câu: 1 Số điểm: 1,0 10 % 5 bài Số câu:8 10,0đ = 100% 4) biên soạn câu hỏi theo ma trận Bài 1: ( 2 đ ) Cho tứ giác ABCD có = 1000, = 500, = 1300. Tính số đo ? Tứ giác ABCD là hình gì? Vì sao? Bài 2: ( 1 đ) Tìm x trên hình vẽ sau: 8cm 16cm x ( AB // DC) Bài 3: (2 đ ) Cho hình Thoi ABCD có AC = 8cm, BD = 6cm. Tính độ dài cạnh hình thoi ABCD Bài 4: 2(đ) Cho rABC cân tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB, AC. a) Chứng minh tứ giác BCNM là hình thang cân. b) Cho BC = 10cm. Tính cạnh MN. Bài 5: (3đ) Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. a) Chứng minh tứ giác EFGH là hình bình hành. b) Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH trở thành hình Vuông? 5) Xây dựng hướng dẫn chấm ( đáp án ) và thang điểm ĐÁP ÁN BIỂU ĐIỂM Bài 1 (2đ): a) Trong tứ giác ABCD có: =>1000 + 500 + 1300+ = 3600 => = 800 b) Tứ giác ABCD có : ( hoặc => AB // CD => Tứ giác ABCD là hình thang (0.5đ) (0.25đ) (0.25đ) (0.5đ) (0.5đ) Bài 2 ( 1đ): Áp dụng tính chất đường trung bình của hình thang ta có (0.5đ) (0.5đ) Bài 3 (2đ): Gọi O là giao điểm của hai đường chéo AC và BD Theo tính chất của hình thoi cĩ: OB = ; OA = Áp dụng định lí Py-ta – go trong tam giác vuông ABO AB = (cm) (1,0đ) (0.5đ) (0.5đ) Bài 4 (2đ): a) MN là đường trung bình của rABC nên MN//BC. Kết hợp với (rABC cân tại A) Ta suy ra BCNM là hình thang cân MN là đường trung bình của rABC nên MN = BC:2 = 5cm (0.5đ) (0.25đ) (0.25đ) (1,0đ) Bài 5 (3đ): HS vẽ hình ghi giả thiết kết luận a) EF, GH lần lượt là đường trung bình của rABC và rADC nên EF//=AC:2; GH//=AC:2 EF//=GHEFGH là hình bình hành b) Tứ giác ABCD cĩ ACBD và AC = BD thì EFGH trở thành hình vuơng (0.25đ) (1,0 đ) (0,75 đ) (1,0đ) 6 Kết quả bài kiểm tra : Lớp Sĩ ố Giỏi Khá TB Trên TB Yếu Kém Dưới TB 8A1 8A2 7 .Nhận xét: 8 .Biện pháp:
Tài liệu đính kèm:
 giao_an_mon_hinh_hoc_lop_8_tiet_24_kiem_tra_chuong_i_nam_hoc.doc
giao_an_mon_hinh_hoc_lop_8_tiet_24_kiem_tra_chuong_i_nam_hoc.doc





