Giáo án Hình học Lớp 9 - Tiết 57: Kiểm tra chương 3 - Năm học 2011-2012 - Nguyễn Huy Du

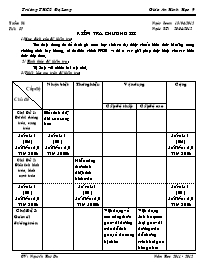
Ngaøy Soaïn: 15/ 04/2012
Ngaøy KT: 20/04/2012
Tuaàn: 31
Tieát: 57
KIEÅM TRA CHÖÔNG III
1/Muïc ñích cuûa ñeà kieåm tra:	
Thu thaäp thoâng tin ñeå ñaùnh giaù xem hoïc sinh coù ñaït ñöôïc chuaån kieán thöùc kó naêng trong chöông trình hay khoâng, töø ñoù ñieàu chænh PPDH vaø ñeà ra caùc giaûi phaùp thöïc hieän cho caùc kieán thöùc tieáp theo.
 2/ Hình thöùc ñeà kieåm tra : 
 Töï luaän vôùi nhieàu baøi taäp nhoû.
3/ Thieát laäp ma traän ñeà kieåm tra: 
 Cấp độ
Chủ đề 
Nhaän bieát
Thoâng hieåu
Vaän duïng
Coäng
Caáp ñoä thaáp
Caáp ñoä cao
Chuû Ñeà 1:
Ñoä daøi ñöôøng troøn, cung troøn 
Bieát tính doä daøi của cung tròn 
Soá caâu: 1
(B2)
Soá ñieåm: 2,0
Tæ leä 20%
Soá caâu: 1
(B1)
Soá ñieåm: 2,0
Tæ leä 100%
Soá caâu: 1
(B2)
Soá ñieåm: 2,0
Tæ leä 20%
Chuû Ñeà 2:
Ñieän tích hình troøn, hình quaït troøn
Hieåu coâng thöùc tính dieän tích hình troøn 
Soá caâu: 1
(B1)
Soá ñieåm: 2,0
Tæ leä 20%
Soá caâu: 1
(B1)
Soá ñieåm: 2,0
Tæ leä 100%
Soá caâu: 1
(B1)
Soá ñieåm: 2,0
Tæ leä 20%
Chuû Ñeà 3:
Goùc vôùi ñöôøng troøn 
Vaän duïng veà caùc coâng thöùc goùc vôùi ñöôøng troøn ñeå tính goùc, soá ño cung bò chaén 
Vaän duïng linh hoaït caùc loaïi goùc vôùi ñöôøng troøn ñeå chöùng minh hai goùc baèng nhau 
Soá caâu: 1
(B3 a,b;B4b)
Soá ñieåm: 4
 Tæ leä 40%
Soá caâu: 1
(B3 a,b)
Soá ñieåm: 3
 Tæ leä 75%
Soá caâu: 1
(B4 b)
Soá ñieåm: 1
 Tæ leä 25%
Soá caâu: 1
(B3 a,b;B4b)
Soá ñieåm: 4
 Tæ leä 40%
Chuû Ñeà 4:
Töù giaùc noäi tieáp 
Chöùng minh ñöôïc töù giaùc noäi tieáp ñöôøng troøn
Soá caâu: 1
(B4 a)
Soá ñieåm: 2
 Tæ leä 20%
Soá caâu: 1
(B4 a)
Soá ñieåm: 2
 Tæ leä 100%
Soá caâu: 1
(B4 a)
Soá ñieåm: 2
 Tæ leä 20%
4 baøi
 soá caâu: 6
Toång soá 
ñieåm 10,0
Tæ leä : 100%
Soá caâu: 1
Soá ñieåm: 2,0 
20 %
Soá caâu:1
Soá ñieåm: 2,0 
 20 %
Soá caâu: 3
Soá ñieåm: 5,0 
 50 %
Soá caâu: 1
Soá ñieåm: 1,0 
 10 %
4 baøi 
Soá caâu: 6
10,0ñ = 100%
4) Biên soạn câu hỏi theo ma trận
Baøi1(2đ): Tính dieän tích cuûa moät hình troøn coù ñöôøng kính 10 cm.
Baøi 2 (2ñ): Tính ñoä daøi cung 300 cuûa moät ñöôøng troøn coù baùn kính 4dm 
Baøi 3 (3ñ): Cho đường tròn (O) đường kính AB = 4cm, vẽ tiếp tuyến Ax, trên Ax lấy điểm C sao cho AC = AB. Gọi M là giao điểm của BC với đường tròn (O).
a) Tính số đo góc CAM và số đo cung nhỏ MB.
b) Tam giác AMB là tam giác gì?
Baøi 4 (3ñ): Cho nửa (O) đường kính AB. Hai điểm C, D nằm trên nửa đường tròn ấy, sao cho C nằm giữa A và D. AC và BD cắt nhau tại E, AD và BC cắt nhau tại F. Chứng minh:
Tứ giác ECFD nội tiếp.
b) 
5) Xây dựng hướng dẫn chấm ( đáp án ) và thang điểm
 ĐÁP ÁN
BIỂU ĐIỂM
Baøi1 (2,0ñ): : r = d/2 = 10/2 = 5 (cm)	
 S = .r2 = 25 (cm2)	
(1.0 ñ)
(1.0 ñ)
Baøi2 (1,5ñ): Áp dụng công thức: 
 l = = 
 = (dm) 
(1.0 ñ)
(1.0 ñ)
Baøi3 (3ñ ):Veõ hình ghi GT, KL ñöôïc 
 a) AC = AB và AC ^ AB (gt) Þ DCAB vuông cân tại A	
 Suy ra = 450 	
 Ta có = 450 (góc nội tiếp và góc giữa tiếp tuyến và một dây cùng chắn một cung). Từ đó suy ra sđ= 900 
 b) = 900 (góc nội tiếp chắn nửa đường tròn) = 450 	
 Suy ra DAMB vuông cân tại M	
(0.5ñ)
(0,5ñ)
(1.0ñ)
(0.5ñ)
(0.5ñ)
Baøi4 (3ñ): Veõ hình ghi GT, KL 
	 a) Xét nửa ( O; ) có:( Góc nội tiếp chắn nửađtròn đkính AB )
Suy ra: Tứ giác ECFD nội tiếp đtròn đkính EF 
( Dấu hiệu nhận biết tứ giác nội tiếp ) 
Hay bốn diểm E, C, F, D cùng thuộc một đtròn
b) Xét đtròn đkính EF có: ( Hệ quả góc nội tiếp ). Xét nửa ( O; ) có: ( Hệ quả góc nội tiếp )
Suy ra: (đpcm)
(0.5ñ)
(0.5ñ)
(0,5ñ)
 (0,5ñ)	 
 (0,5ñ)
 (0,5ñ)
6 Keát quả bài kiểm tra :
Lôùp
Sĩ soá
Gioûi
Khaù
TB
Treân TB
Yeáu
Keùm
Döôùi TB
9A1
26
9A2
26
 7 .Nhaän xeùt:
8 .Bieän phaùp: