Giáo án Hình học Lớp 8 - Tiết 7 đến 10 - Ngô Thanh Hữu

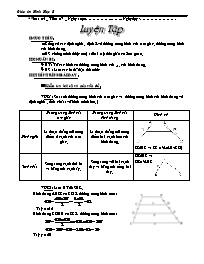
Tuần : 04 _ Tiết : 07 _ Ngày soạn:....Ngày dạy:
Luyện Tập 
I.MỤC TIÊU : 
@ Củng cố các định nghĩa, định lí về đường trung bình của tam giác, đường trung bình của hình thang.
@ HS chứng minh được một số bài tập đơn giản có liên quan.
II.CHUẨN BỊ : 	
 Ä GV: Vẽ các hình có đừơng trung bình của ∆ , của hình thang.
 Ä HS : Làm các bt đã dặn tiết trước 
III.TIẾN TRÌNH BÀI DẠY :
 Kiểm tra bài cũ và nêu vấn đề : 
* HS1 : So sánh đường trung bình của tam giác và đường trung bình của hình thang về định nghĩa , tính chất ( vẽ hình minh hoạ )
Đường trung bình của tam giác
Đường trung bình của hình thang
Hình vẽ
Định nghĩa
Là đoạn thẳng nối trung điểm 2 cạnh của tam giác.
Là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
EF//BC và EF = ½(AB+CD)
Tính chất
Song song cạnh thứ ba và bằng nửa cạnh ấy.
Song song với hai cạnh đáy và bằng nửa tổng hai đáy.
DE//BC và 
DE= ½BC
* HS2 : Làm BT 26 SGK.
 Hình thang ABFE có CD là đường trung bình nên :
	 Vậy x =12
 Hình thang CDHG có EF là đường trung bình nên : 
	 Vậy y = 20
‚ Luyện tập : 
Trợ giúp của giáo viên
Hoạt động của học sinh
* GV cho HS làm bài tập 25 SGK.
+ YeÂu cầu HS tự vẽ hình.
+ Vận dụng định lý về đường trung bình vủa hình thang và tiên đề Ơclit.
* GV vẽ sẵn hình, yêu cầu HS lên ghi GT, KL.
a) Với gt đã cho thì EK có phải là đường trung bình của ∆ ADC ? Từ đó suy ra điều gì ?
* KF có phải là đường trung bình của ∆ ABC ? Từ đó suy ra điều gì ?
b) Xét ∆ EKF ta có điều gì ?
à áp dụng định lí 4 c/m tiếp.
* GV gọi HS lên vẽ hình , ghi GT, KL.
a) EF có phải là đường trunh bình của hình thang ABCD hay không?
+ Xét tiếp các ∆ ADC, BDC => điều chứng minh
b) GV gợi ý HS áp dụng định lí 2, định lí 4 về đường trunh vbình của ∆ , của hình thang để chứng minh.
* Bài tập 25 / SGK 
+ HS về nhà trình bày lại cách giải và tìm cách giải khác của bài tập 25
* Bài tập 27 / SGK 
* EK là đường trung bình của ∆ ADC vì E, K là các trung điểm => 
* KF có phải là đường trung bình của ∆ ABC. 
=> 
* EF EK + KF 
* Bài tập 28 / SGK 
* 1 HS lên vẽ hình , ghi GT, KL.
+ EF là đường trung bình của hình thang ABCD vì E , F là các trung điểm của cạnh bên.
+ HS áp dụng định lí 1 về đường trunh bình của ∆ để chứng minh.
* 1 HS lên bảng làm.
25) Theo giảthiết ta có :
EK là đường trung bình 
của ∆ ABD => EK // AB (1)
EF là đường trung bình 
của hình thang ACBD
 => EF // AB // CD (2)
Từ (1) và (2) => EF và EK cùng đi qua một trung điểm E và song song với AB, theo tiên đề ơclic suy ra EK và EF trùng nhau.
Vậy, E , K, F thẳng hàng.
27)
GT tứ giác ABCD
 AE = AD, BF = FC
 AK = KC.
KL a) so sánh EK và CD
 So sánh KF và AB
 b) 
Chứng minh:
a) EK là đường trung bình của ∆ ADC 
=> 
 KF là đường trung bình của ∆ ABC 
=> 
b) Ta có : EF EK + KF (1)
mà (2)
Từ (1) và (2) suy ra : (đpcm)
28)
GT hình thang ABCD 
 (AB // CD)
 AE = ED, BF = FC
 AB = 6cm, CD = 10cm
KL a) AK = KC, BI = ID
 b) Tính EI, KF, IK.
Chứng minh:
a) Ta có EF là đường trung bình của hình thang ABCD => EF // AB // CD .
* Xét ∆ ADC có: AE = ED và EK // CD 
=> AK = KC
* Xét ∆ BDC có: BF = FC và FI // CD 
=> BI = ID
b) EI là đường trung bình của ∆ ABD
=> 
 FK là đường trung bình của ∆ ABC
=> 
 EF là đường trung bình của hình thang ABCD
=> 
 => IK = EF – (EI + FK) = 8cm – 6cm = 2cm
ƒ Dặn dò : 
ð Tìm cách chứng minh khác của bài tập 25 / SGK.
ð Xem lại các định lí , định nghĩa về đường trung bình của tam giác, của hình thang đã học.
ð Tiết sau mang theo đầy đủ com pa và thước thẳng. Xem trước bài 5.
Tuần : 04 _ Tiết : 08 _ Ngày soạn:....Ngày dạy:
Bài 5: Dựng Hình Bằng Thước và Compa.
DỰNG HÌNH THANG
I.MỤC TIÊU : 
@ HS biết dùng thước và compa để dựng hình thang theo các yếu tố đã cho. Biết trình bày hai phần : cách dựng và chứng minh.
@ Rèn luyện tính cẩn thận ,chính xác khi sử dụng dụng cụ ,rèn luyện khả năng suy luận , có ý thức vận dụng dựng hình vào thực tế.
II.CHUẨN BỊ : 	
 Ä GV +HS : Thước thẳng + compa.
III.TIẾN TRÌNH BÀI DẠY :
 Giới thiệu bài: 
 Ở lớp 6 và lớp 7 học sinh đã được làm quen với những bài toán dựng hình đơn giản như : vẽ đoạn thẳng bằng đoạn thẳng cho trước, vẽ một góc bằng một góc cho trước, vẽ đường trung trực của một đoạn thẳng cho trước, vẽ tia phân giác của một góc cho trước, vẽ tam giác biết ba cạnh, biết hai cạnh và góc xen giữa, biết một cạnh và hai góc kề ...
	Trong bài này ta chỉ xét các bài toán vẽ hình mà chỉ sử dụng hai dụng cụ là thước và compa, chúng được gọi là các bài toán dựng hình.
‚ Bài mới : 
Trợ giúp của giáo viên
Hoạt động của học sinh
Trình bày bảng
Hoạt động 1 : Tìm hiểu bài toán dựng hình cơ bản
*Thước thẳng có tác dụng gì ?
*Còn compa có tác dụng gì ?
* HS xem SGK và trả lời.
1) Bài toán dựng hình :
_ Tác dụng của thước thẳng :
+ Vẽ một đường thẳng khi biết hai điểm.
+ Vẽ một đoạn thẳng khi biết hai đầu mút.
+ Vẽ một tia khi biết gốc và một điểm của tia.
_ Tác dụng của compa : Vẽ đường tròn hoặc cung tròn khi biết tâm và bán kính của nó.
Hoạt động 2 : Các bài toán dựng hình đã biết
* GV nêu lại bài toán dựng hình đã học ở lớp 7 bằng thước thẳng và compa.
* GV biểu diễn dựng lại các hình cơ bản: đoạn thẳng, dựng góc bằng góc cho trước, dựng đường trung trực đoạn thẳng, dựng trung điểm, dựng tia phân giác; qua 1 điêm nằm ngoài đường thẳng cho trước dựng đường thẳng // (hoặc vuông góc ) với đường thẳng đã cho ; dựng tam giác.
Hoạt động 3 : Tìm hiểu dựng hình thang
a) + Trước tiên ta giả sử là hình đã dựng được rồi thoả mãn yêu cầu bài toán. Đồng thời vẽ nháp hình thang đó ra giấy.
+ Bộ phận nào có thể dựng được ngay ?
+ Vậy, hình thang ABCD đã có AD = 2cm, DÂ = 700 và CD = 4cm. Còn lại phải dựng đáy AB = 3cm à Điểm B phải thoả mãn điều kiện gì?
b) + Dựa vào các bước phân tích trên, hãy tiến hành dựng hình theo tuần tự.
c) Bằng lập luận hãy chững tỏ rằng hình vừa dựng được có đủ các yếu tố của đề bài đưa ra.
+ Theo cách dựng, tứ giác ABCD là hình gì? Có đủ các yếu tố của bài toán yêu cầu không ?
d) Biện luận : Xét xem khi nào thì bài toán dựng được, và dựng được mấy hình thoả mãn yêu cầu bài toán.
* HS xem SGK để nhớ lại các bài toán dựng hình cơ bản đã học ở lớp 7.
* HS chú ý theo dõi.
* 1 vài HS đọc đề bài toán.
+ HS thực hiện vẽ nháp hình thang ABCD có các yếu tố bài toán yêu cầu.
+ ∆ ADC dựng được ngay vì biết độ dài 2 cạnh và góc xen giữa.
+ B thuộc đường thẳng đi qua A và // với CD.
+ B cách A một khoảng 3cm.
* HS thực hiện theo hướng dẫn của GV.
+ Theo cách dựng, tứ giác ABCD là hình thang có đủ các yếu tố bài toán yêu cầu.
d) HS nhận xét : Ta dựng được bao nhiêu hình thang như thế.
+ HS thực hiện dựng hình.
2) Các bài toán dựng hình đã biết:
Dựng đoạn thẳng bằng đoạn thẳng cho trước.
Dựng một góc bằng một góc cho trước.
Dựng đường trung trực của một đoạn thẳng cho trước, dựng trung điểm của một đoạn thẳng cho trước.
Dựng tia phân giác của một góc cho trước.
Qua một điểm cho trước dựng đường thẳng vuông góc với một đường thẳng cho trước.
Qua một điểm nằm ngoài một đường thẳng cho trước, dựng đường thẳng song song với một đường thẳng cho trước.
Dựng tam giác biết ba cạnh, biết hai cạnh và góc xen giữa, biết một cạnh và
hai góc kề.
3) Dựng hình thang :
Ví dụ : Dựng hình thnag ABCD biết đáy AB = 3cm, đáy CD = 4cm , cạnh bên AD= 3cm , DÂ = 700 .
Giải:
a) Phân tích:
 Giả sử đã dựng được hình thang thoả mãn yêu cầu đề bài.
- ∆ ADC dựng ddwowjc vì biết 2 cạnh và góc xen giữa.
- Do ABCD là hình thang nên điểm B phải thoả mãn hai điều kiện :
 + B thuộc đường thẳng đi qua A và // với CD.
 + B cách A một khoảng 3cm.
b) Cách dựng :
- Dựng ∆ ADC có AD = 2cm, DÂ = 700 và DC = 4cm.
- Dựng tia Ax // CD (tia Ax và điểm C cùng nằm trong một nửa mặt phẳng bờ AD).
- Dựng B Ax sao cho AB = 3cm. 
- Kẻ BC.
c) Chứng minh :
Theo cách dựng, tứ giác ABCD là hình thang vì AB // CD.
Hình thang có AB = 2cm, CD = 4cm, 
AD = 2cm, DÂ = 700 nên thoả mãn yêu cầu đề bài.
d) Biện luận :
Ta dựng được một hình thang thoả mãn yêu cầu bài toán.
ƒ Củng cố : 
 Ä BT 29 / SGK.
Cách dựng :
Dựng đoạn thẳng BC = 4cm
Dựng CBx = 650
Dựng CA 
(bằng cách dựng đường thẳng đi qua C và vuông góc với Bx) 
Chứng minh :
	 có Â = 900, BC = 4cm, thỏa mãn đề bài.
„ Dặn dò : 
ð Xem thật kỹ bài toán dựng hình trong SGK.
 ð BTVN : 30, 31, 32, 33, 34 / SGK.
Tuần : 05 _ Tiết : 09 _ Ngày soạn:....Ngày dạy:
I.MỤC TIÊU : 
@ Củng cố cách dựng hình bằng thước và compa.
@ HS dựng được hình thang bằng thước và compa.
@ Yêu cầu chủ yếu HS dựng được tia phân giác của góc, dựng đường trung trực của đoạn thẳng.
II.CHUẨN BỊ : 	
 Ä GV + HS : Thước thẳng, compa, thước đo góc.
III.TIẾN TRÌNH BÀI DẠY :
 Kiểm tra bài cũ: 
Nêu các bước làm một bài toán dựng hình?
 - Bài tập 30 / SGK.
Cách dựng :
Dựng đoạn thẳng BC = 2cm 
Dựng CBx = 900
Dựng cung tròn tâm C bán kính 4cm, cắt tia Bx ở A.
Dựng đoạn thẳng BC
Chứng minh :
	 có , AC = 4cm, BC = 2cm
thỏa mãn đề bài.
‚ Luyện tập : 
Trợ giúp của giáo viên
Hoạt động của học sinh
* GV gọi một vài HS đọc đề bài.
* Như thế nào gọi là hình thang cân ?
* Bước 1 của bài toán dựng hình như thế nào?
à GV hướng dẫn HS từng bước dựng hình thang.
* GV hướng dẫn HS như bài trên.
 +Tam giác nào dựng được ngay ? vì sao ?
 + Đỉnh B được dựng như thế nào ?
* Lưu ý HS phần biện luận : Cung tròn tâm C bán kính 3cm cắt tia Ax tại 2 điểm B và B’ . Vậy ta có 2 nghiệm hình thang thoả mãn yêu cầu bài toán là : ABCD và AB’CD.
* Dựng góc 300 chỉ dùng thước và compa.
* Hãy dựng góc 600 trước. Làm thế nào để dựng góc 600 bằng thước và compa?
* Để có goá 300 ta phải làm như thế nào ?
* Bài tập 33 / SGK 
* một vài HS đọc đề bài.
* Hình thang cân là hình thang có 2 góc kề một đáy bằng nhau. (Hình thang có 2 đường chéo bằng nhau cũng là hình thang cân)
* Ta giả sử hình thang đã dựng được rồi. Vẽ hình ngoài nháp và từng bước phân tích.
* HS thực hành dựng hình theo sự hướng dẫn.
* Bài tập 34 / SGK
+ Tam giác ADC vì biết hai cạnh và một góc.
+ Dựng cung tròn tam C bán kính 3cm
*BT 32 SGK
*Dựng tam giác đều.
*Dựng tia phân giác của một góc trong tam giác đều.
 33) *Cách dựng 
Giả sử đã dựng được hình 
Thang ABCD thoả mãn
yêu cầu bài toán.
- Dựng đoạn thẳng 
CD = 3cm
- Dựng CDÂx = 800 ,
- Dựng cung tròn tâm C bán kính 4cm, cắt Dx ở A.
- đựng tia Ay // DC sao cho tia Ay và C nằm trên cùng một nửa mặt phẳng bờ AD.
- Dựng điểm B Ay. Có 2 cách:
 + Dựng đường tròn tâm D bán kính 4cm.
 + Hoặc: Dựng góc DCÂz = 800 .
*Chứng minh
_ Tứ giác ABCD là hình thang vì AB // CD
_ Hình thang ABCD có CD = 3cm, , AC = 2cm
_ Hình thang ABCD còn có nên là hình thang cân
34) *Cách dựng :
Giả sử đã dựng
được hình thang
ABCD thoả mãn 
yêu cầu bài toán.
- Dựng ∆ ADC
vuông ở D và có
DA = 2cm, DC = 3cm.
- Dựng tia Ax // DC ( tia Ax và C cùng nằm trên một nửa mặt phẳng bờ AD). 
- Dựng B Ax bằng cách dựng đường tròn tâm C bán kính 3cm.
* Chứng minh
ABCD là hình thang vì AB//CD có AD = 2cm , góc D = 900 , DC = 3cm , BC = 3cm thoả mãn yêu cầu của đề bài.
32) *Cách dựng :
-Dựng một tam giác đều có cạnh tuỳ ý và có góc 600.
-Dựng tia phân giác của góc 600 ta được góc 300. C
) 300
 A B
*Chứng minh ( HS tự làm) 
ƒ Dặn dò: 	ð Xem lại các bước dựng hình. 
ð Tập làm lại các bài toán dựng hình đã sửa. 
ð Xem trước bài học kế tiếp “Đối xứng trục”. 
ð Xem lại các định nghĩa đ.t.trực của đoạn thẳng, ∆ cân, ∆ đều, hình thang cân.
Tuần : 05 _ Tiết : 10 _ Ngày soạn:....Ngày dạy:
Bài 6 . ĐỐI XỨNG TRỤC 
I.MỤC TIÊU : 
@ HS hiểu định nghĩa 2 điểm đối xứng nhau qua đường thẳng. Nhận biết được hai đoạn thẳng đối xứng với nhau qua một đường thẳng.
@ HS biết vẽ một điểm đối xứng với một điểm cho trước; đoạn thẳng đối xứng với một đoạn thẳng cho trước.
@ HS biết nhận ra một số hình trong thực tế có trục đối xứng như: ∆ cân, hình thang cân đường tròn 
II.CHUẨN BỊ : 	
 Ä GV: Bảng phụ hình 53, 54, tấm bìa cứng chữ A , tam giác đều , hình tròn, hình thang cân.
 Ä HS : Thước thẳng, compa, tấm bìa cứng hình thang cân.
III.TIẾN TRÌNH BÀI DẠY :
 Nêu vấn đề : 
Cho học sinh quan sát hình 49 trang 84. Hỏi : Muốn cắt chữ H như trong hình 49 ta có thể gấp tờ giấy làm tư. Tại sao vậy ?
 Câu trả lời sẽ được giải đáp trong bài học sau đây.
‚ Bài mới : 
Trợ giúp của giáo viên
Hoạt động của học sinh
Trình bày bảng
Hoạt động 1 : Thế nào là hai điểm đối xứng nhau qua một đường thẳng ?
* GV giới thiệu: Theo hình vẽ, dường thẳng d là gì của đoạn thẳng AA’ ?
à Khi đó ta nói hai điểm A và A’ đối xứng với nhau qua đường thẳng d.
* Quy ước: Nếu điểm B nằm trên đường thẳng d thì điểm đối xứng với điểm B qua d cũng chính là điểm B.
Hoạt động 2 : Hai hình đối xứng nhau qua một đường thẳng là như thế nào ?
* Hãy xem hình 32: Có phải mọi điểm thuộc đoạn thẳng AB đều có điểm đối xứng thuộc đoạn thẳng A’B’ và ngược lại ?
*GV treo bảng phụ hình 53 và hình 54 SGK để giới thiệu về hai đoạn thẳng, hai góc, hai tam giác, 2 hình H và H 
đối xứng nhau qua đường thẳng d.
* Sau đó yêu cầu HS rút ra nhận xét.
*Muốn dựng một đoạn thẳng đối xứng hay một tam giác đối xứng nhau qua một đường thẳng ta phải làm sao ?
Hoạt động 3 : Thế nào là hình có trục đối xứng ?
*Cho HS làm ?3 SGK
* GV giới thiệu như SGK.
* GV giới thiệu định lí trục đối xứng của hình thang cân.
* Cho HS làm ?4 SGK
* Bài tập ?1 / SGK 
* d là đường trung trực của đoạn thẳng AA’.
* HS ghi định nghĩa và vẽ hình (có thể chừa trống về nhà ghi)
* Bài tập ?2 / SGK 
* Mọi điểm thuộc đoạn thẳng AB đều có điểm đối xứng thuộc đoạn thẳng A’B’ và ngược lại.
* HS nêu ĐL trong SGK.
* Dựng đối xứng từng điểm và nối lại.
* Bài tập ?3 / SGK 
_ Hình đối xứng với cạnh AB qua đường cao AH là AC.
_ Hình đối xứng với cạnh AC qua đường cao AH là AB.
_ Hình đối xứng với đoạn BH qua đường cao AH là CH và ngược lại.
* Bài tập ?4 / SGK
a) Chữ cái in hoa A có một trục đối xứng.
b) Tam giác đều ABC có 3 trục đối xứng.
c) Đường tròn tâm O có vô số trục đối xứng.
1) Hai điểm đối xứng qua 
một đường thẳng:
* Định nghĩa:
 Hai điểm gọi là đối xứng
với nhau qua đường thẳng d
nếu d là đường trung trực của đoạn thẳng đó.
2) Hai hình đối xứng qua một đường thẳng :
* Định nghĩa :
 Hai hình được gọi làđối xứng với nhau 
qua đường thẳng d nếu mỗi điểm thuộc
hình này đối xứng với một điểm thuộc hình kia và ngược lại.
* Đường thẳng d gọi là trục đối xứng.
* Định lí:
 Nếu hai đoạn thẳng ( góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
3) Hình có trục đối xứng :
 Nếu mọi điểm thuộc hình 
H đều có điểm đối xứng qua 
đường thẳng d cũng thuộc 
hình H thì đường thẳng d
 gọi là trục đối xứng của
hình H.
* Định lí :
 Đường thẳng d qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ƒ Củng cố : 
Ä Bài tập 37 / SGK
	® Hình 59h không có trục đối xứng, còn tất cả các hình khác đều có trục đối xứng
„ Lời dặn : 
ð Xem kĩ bài vừa học.
ð BTVN : 36, 38, 39, 40, 41 / SGK.