Đề kiểm tra Hình học Lớp 8 - Chương I - Trường THCS Tân Xuân

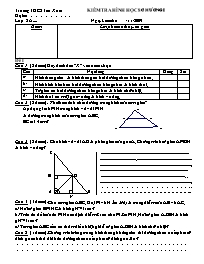
Trường THCS Tân Xuân	KIỂM TRA HÌNH HỌC 8 CHƯƠNG I
Họ tên:
Lớp : 8A....	 Ngày kiểm tra: /11/2009
Điểm
Lời phê của thầy, cơ giáo
Đề I: 
Câu 1: (2 điểm) Hãy đánh dấu “X” vào ơ em chọn:
Câu
Nội dung
Đúng
Sai
a/
Hình thang cân là hình thang có hai đường chéo bằng nhau.
b/
Hình bình hành có hai đường chéo bằng nhau là hình thoi.
c/
Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
d/ 
Hình thoi có một góc vuông là hình vuông.
Câu 2: (2 điểm) . Phát biểu tính chất đường trung bình của tam giác? 
Áp dụng: Tính MN trong hình vẽ với MN là đường trung bình của tam giác ABC, 
BC = 14 cm?
Câu 3: (2 điểm) . Cho hình vẽ với AD là phân giác của góc A. Chứng minh tứ giác AMDN là hình vuông? 
 C  
 .
 .
 M D .. 
 .
 ..
 A B ..
 N 
Câu 4: (3 điểm). Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC.
a/ Hỏi tứ giác BMNC là hình gì? Vì sao?
b/ Trên tia đối của tia MN xác định điểm E sao cho ME = MN. Hỏi tứ giác AEBN là hình gì? Vì sao?
c/ Tam giác ABC cần có thêm điều kiện gì để tứ giác AEBN la hình chữ nhật? 
Câu 5: (1 điểm). Chứng minh rằng trong hình thang không cân thì đường chéo xuất phát từ đỉnh góc nhỏ sẽ dài hơn đường chéo xuất phát từ đỉnh góc lớn?
Trường THCS Tân Xuân	KIỂM TRA HÌNH HỌC 8 CHƯƠNG I
Họ tên:
Lớp : 8A....	 Ngày kiểm tra: /11/2009
Điểm
Lời phê của thầy, cơ giáo
Đề II: 
Câu 1: (2 điểm). Phát biểu tính chất đường trung bình của hình thang? 
Áp dụng: Tính EF trong hình vẽ , biết EF là đường trung bình của hình thang ABCD (AB // CD) và AB = 8cm, CD = 12cm
 Câu 2: (2 điểm) Khoanh tròn vào kết quả ,em cho là đúng nhất:
 Cho hình vẽ bên ,biết AB= 4 cm; AC=3 cm
 a/ Độ dài đọan thẳng BC là :
 A.5cm B.6cm 	 C.4cm
 b/ Độ dài đọan thẳng AM là:
 A. 2cm	. B.3cm	C.2,5cm
Câu 3: (2 điểm) . 
Cho hình vẽ bên biết DN // AB,DM // AC,AD là phân giác của góc A.Chứng minh tứ giác AMDN là hình thoi? 
Câu 4: (3 điểm) . Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng với M qua I.
a/ Tứ giác AIMB là hình gì? Vì sao?
b/ Tứ giác AKMB là hình gì? Vì sao?
c/ Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông?
Câu 5: (1 điểm) .Cho tam giác ABC đều, M là một điểm tùy ý nằm trong tam giác .Chứng minh tổng khoảng cách từ M tới các cạnh của tam giác luôn không đổi?
Bài làm
ĐÁP ÁN BIỂU ĐIỂM
Đề I: 
Câu 1: Mỗi ý đúng 0,5 điểm:	a – Đ;	b – S;	c – S;	d - Đ
Câu 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Aùp dụng: Do MN là đường trung bình của tam giác ABC nên ta có:
 MN = , mà BC = 14 cm ;
Câu 3: Xét tứ giác AMCN có: 
 Do đó tứ giác AMCN là hình chữ nhật.
 Hình chữ nhật AMCN có AD là tia phân giác của góc A, nên hình chữ nhật AMCN là hình vuông.
Câu 4:
a/ Xét tứ giác BMNC có: 
 MA = MB (gt), NA = NC (gt)
 Nên MN là đường trung bình của ABC.
MN // BC (tính chất đường trung bình của tam giác)
Vậy tứ giác BMNC là hình thang.
b/ Xét tứ giác ANBE có: AB cắt EN tại M
MN = ME (gt), MA = MB (gt)
Do đó tứ giác ANBE là hình bình hành.
c/ Tứ giác ANBE là hình chữ nhật khi hình bình hành ANBE có => BN là trung tuyến đồng thời là đường cao.Vậy ABC phải cân tại B.
Câu 5: 
Xét hình thang ABCD có góc D nhỏ hơn góc C.
Dựng hình thang cân A’BCD.
Do góc D nhỏ hơn góc C nên A’ nằm trên tia đối của tia AB.
Khi đó góc A’AC lớn hơn góc B, góc B lớn hơn góc AA’C.Do đó AC < A’C = BD.
Đề II: 
Câu 1: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng độ dài hai đáy.
Aùp dụng: Do EF là đường trung bình của hình thang ABCD nên ta có:
 EF = , mà AB = 8 cm , CD = 12 cm ; 
Câu 2: Mỗi ý đúng 1 điểm:	a – A;	b – C;	
Câu 3: Xét tứ giác AMDN có: 
 , 
 Do đó tứ giác AMDN là hình bình hành.
 Hình bình hành AMDN có AD là phân giác của góc A nên AMDN là hình thoi.	
Câu 4: 
a/ Xét tứ giác AIMB có: IA = IC (gt), MB = MC(gt)
 Nên IM là đường trung bình của ABC.
IM // AB (tính chất đường trung bình của tam giác)
Vậy tứ giác AIMB là hình thang.
b/ Xét tứ giác AKCM có: AC cắt KM tại I
IA = IC (gt), MI = IK(gt)
Do đó tứ giác AKCM là hình bình hành.
Hình bình hành AKCM có góc AMC = 900 nên là hình chữ nhật.
c/ Tứ giác AKCM là hình vuông khi hình chữ nhật AKCM có MA = MC.Vậy ABC phải vuông tại A.
Câu 5:
Từ M kẻ đường thẳng song song với BC cắt AB tại B’,AC tại C’, khi đó tam giác AB’C’ là tam giác đều,
Ta lại có IN = MN’( tứ giác MINN’ là hình chữ nhật)
=> MK + MH = AN’(AN’ là đường cao của tam giác đều AB’C’)
Do đó MI + MK + MH = MI + AN’ = NN’ + AN’ = AN không đổi.