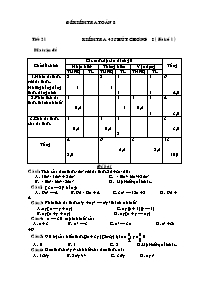
Đề kiểm tra 45 phút môn Toán Lớp 8 - Tiết 21

 Đề kiểm tra toán 8
 Tiết 21 kiểm tra 45 phút- chương i ( Bài số 1)
 Ma trận đề
Chủ đề chính
 Các mức độ cần đánh giá
Tổng
Nhận biết
Thông hiểu
Vận dụng
TMKQ
 TL
TMKQ
TL
TNKQ
TL
 1. Nhân đa thức với đa thức. Những hằng đẳng thức đáng nhớ
2
 1 
2
 1 
1
 1
1
 1
6
 4,0
 2. Phân tích đa thức thành nhân tử
1
 0,5
1
 1
1
 0,5
1
 1
4
 3,0
 3. Chia đa thức cho đa thức
1
 0,5
1
 0,5
1
 2
3
 3,0
 Tổng 
4
 2,0
6
 5,5
3
 2,5
13
 10,0
Đề bài
Câu1: Tích của đơn thức -5x3 với đa thức 2x2+3x -5 là: 
 A. 10x5- 15x4 + 25x3 C. -10x5-15x4+25x3
 B. -10x5-15x4 -25x3 D. Một kết quả khác.
 Câu2: ( 3x – 2)2 bằng:
 A. 9x2 – 4 B. 9x2 -12x + 4 C. 3x2 – 12x + 2 D. 9x2 + 4
 Câu 3: Phân tích đa thức x2y + xy2 – x2y2 thành nhân tử
 A. xy( x – y + xy) C. xy(x + 1)(y – 1)
 B. xy( x + y + xy) D. xy( x + y – xy)
 Câu 4: x – 3 là một nhân tử của 
 A. x + 3 B. x2 – 3 C. x2 – 3x D. x2 +6x +9
 Câu 5: Giá trị của biểu thức(2x + 3y)(2x-3y) tại x=; y= là
 A. 0 B. 1 C. 2 D. Một kết quả khác.
 Câu 6: Đơn thức 8x5yz4 chia hết cho đơn thức nào
 A. 16x4y B. 2x2y2z4 C. 3x6y D. xyz5
 Câu 7: Kết quả của phép chia (-x3y3z): (-3x2yz) bằng 
 A. 3y2 B.- C. D. 3 
 Khoanh tròn vào chữ cái trước câu trả lời đúng 
 Câu 8: Điền vào chỗ trống.
 a) 9x2 + 6xy + ... = (... + y)2
 b) 8y3 + ... = ( 2y + x)( ... – 2xy + x2)
 Câu 9: Rút gọn rồi tính giá trị của biểu thức sau tại x= 2008 ; y= -3
 A = (x + y)2 + (x – y)2 – 2(x + y)(x – y)
 Câu 10: Phân tích đa thức sau thành nhân tử
 xy + y2 – x – y
 Câu 11: làm tính chia 
 ( x4 – 2x3 + 2x – 1) : (x2-1)
 Câu 12: Chứng minh : x2 – x + 1 > 0 với mọi số thực x.
Đáp án
 Mỗi câu đúng được 0,5đ
Câu
1
2
 3
 4
5
6
7
Đáp án
C
B
 D
 C
A
Â
C
 Câu 8:
 a) y2 ; 3x (0,5đ)
 b) x3 ;4x2 (0,5đ)
 Câu 9: Kq: A = 4y2 (1đ)
 Thay y= -3 vào A = 4y2 = 4. (-3)2 = 36 (1đ)
 Câu 10: Kq: ( x – 1)( x + y) (1đ) 
 Câu 11: Kq : x2 – 2x + 1 (2đ)
 Câu12: x2 – x + 1= (1đ)
 Tiết 39- 40 Kiểm tra học kì I
 Ma trân đề
Chủ đề chính
 Các mức độ cần đánh giá
Tổng
Nhận biết
Thông hiểu
Vận dụng
TMKQ
 TL
TMKQ
TL
TNKQ
TL
 1. Phép nhân và phép chia đa thức
4
 1 
2
 1
6
 2,0
 2. Phân thức đại số
1
 1,5
2
 1,5 
3
 3,0
 3. Tứ giác và diện tích đa giác
2
 1
3
 4
5
 5,0
 Tổng 
6
 2,0
6
 6,5
2
 1,5
14
 10,0
Đề bài
 Câu 1. Điền dấu "X" vào ô thích hợp
Câu
Nội dung
Đúng
Sai
1
(x-2)2 = x2 - 2x + 4
2
(a-b)2 = a2 - b2
3
-(x + 3)2 = (-x-3)2
4
(x3-8) : (x-2) = x2 + 2x + 4
Câu 2. a) Diện tích hình vuông có cạnh bằng 4cm. 
Diện tích của hình vuông là: ..............................
 b) Tam giác vuông có hai cạnh độ dài hai cạnh góc vuông bằng 4cm và 6cm.
Diện tích của tam giác vuông đó là: .............................
Câu 3. Phân tích các đa thức sau thành nhân tử:
a) x3 + x2 – 4x – 4
b) x2 – 2x – 15
Câu 4. Cho biểu thức:
 A = 
a) Rút gọn A.
b) Tính giá trị của A khi x = 
c) Tìm các giá trị nguyên của x để biểu thức A có giá trị nguyên.
Câu 5. Cho hình bình hành ABCD có BC = 2. AB. Gọi M, N thứ tự là trung điểm của BC và AD. Gọi P là giao điểm của AM với BN, Q là giao điểm của MD với CN, K là giao điểm của tia BN với tia CD.
a) Chứng minh tứ giác MDKB là hình thang.
b) Tứ giác PMQN là hình gì ? Chứng minh ?
c) Hình bình hành ABCD phải có thêm điều kiện gì để PMQN là hình vuông.
Đáp án
 Câu1: (1đ) Mỗi câu 0,25đ
 Câu 2: (1đ) Mỗi câu 0,5đ
 a) 16cm2
 b) 12cm2
 Câu 3: (1đ)
 a) x3 + x2 - 4x – 4 = x2 (x + 1) – 4 (x + 1)
 = ( x +1) (x2 – 4)
 = (x + 1) ( x – 2) ( x + 2) 0,5đ
 b) x2 – 2x – 15 = x2 + 3x – 5x – 15
 = x (x + 3) – 5 (x + 3)
 = (x +3) (x – 5) 0,5đ
 Câu 4: (3đ) a) Rút gọn đúng A = 1,5đ
 b) Tính A khi x = ĐK: ; 0,25đ
 x = thỏa mãn ĐK của x. Thay x = vào A = 0,25đ
 c) Tìm x Z để A Z
A = với ĐK: x; x
A = Có 1 
 0,5đ
 KL: thì A Z 0,5 đ 
 Câu 5: (4 điểm)
 a) Chứng minh được BMND là hình bình hành => MD // BN 1,0đ
 Xét tứ giác MDKB có MD // BK => MDKB là hình thang. 0,5đ 
 b) Chứng minh được tứ giác PMQN là hình chữ nhật. 1,5đ
 c) Tìm được hình bình hành ABCD cần thêm điều kiện có một góc vuông thì PMQN là 
 hình vuông. 1đ
 Tiết 69-70 Kiểm tra cuối năm(90 phút)
 Đề bài
 Câu 1: Hai bất phương trình sau có tương đương không?
 a) x – 3 > 1 và x + 3 > 7 b) -x -7
 Cõu 2: Mỗi bài tập dưới đõy cú nờu kốm cỏc cõu trả lời A, B, C, D. Em hóy chọn và khoanh trũn chữ cỏi đứng trước cõu trả lời đỳng nhất.
1. Tỉ số của hai đoạn thẳng cú độ dài 3dm và 6cm là:
	A. 2 	B. 	C. 5	 	D. Cõu A, B, C đỳng. 
2. Cho cú AB// EF ( A DE, B DF) ta cú kết quả sau đõy:
	A. 	B. 	C. 	 D.Cõu A, B đỳng. 
3. Trong cỏc phỏt biểu sau, phỏt biểu nào đỳng:
	A. Hai tam giỏc bằng nhau thỡ đồng dạng với nhau.
	B. Hai tam giỏc đồng dạng với nhau thỡ không bằng nhau.
	C. Tỉ số diện tớch của hai tam giỏc đồng dạng bằng tỉ số đồng dạng.
 D.Tất cả cỏc cõu trờn đều đỳng. 
4. MN là đường phõn giỏc trong của . Ta cú:
	A. 	B. 	
C. 	D. Tất cả cỏc cõu trờn đều đỳng. 
 Câu 3: Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số
 a) 3x -7 0	 
 b) 
Câu 4 Giải các phương trình sau
 a) (x+2)(3-4x) + (x2+4x+4) = 0
 b) 
 Câu 5: Giải bài toán bằng cách lập phương trình
 Một người đi xe máy từ A đến B với vân tốc 30 km/h .Đến B người đó làm việc trong 1 h rồi quay về A với vận tốc 24 km/h . Biết thời gian tổng cộng hết 5h 30 ph . Tính quãng đường AB
Cõu 6: Cho ABC cú AB = 9cm, AC = 18 cm. Trờn cạnh AB, AC lần lượt lấy cỏc điểm M, N sao cho AM = 2 cm, AN = 4cm.
a. Chứng minh rằng AMN ABC.
b. Biết BC = 18cm. Tớnh độ dài đoạn thẳng MN.
c. Trờn cỏc cạnh AB, AC lần lượt lấy cỏc điểm D, E sao cho BD = CE. Gọi F, G lần lượt là trung điểm của BC, DE; Đường thẳng DF cắt cỏc đường thẳng AB và AC lần lượt tại P và Q. Chứng minh APQ cõn.
. 
 Đáp án
 Câu1: (1đ) 
 a) Là hai phương trình tương đương 0,5d 
 b) Không phải là hai phương trình tương đương 0,5đ
 Câu2:(1đ)
1
2
3
4
C
C
D
B
 Câu3:(1,5đ)
 a) (0,5đ) Kq x 0,25đ
 Biểu diễn tập nghiệm 0,25đ 
 b) (1đ) Nếu x
 Do đó ) 2x – 1 < x + 1
	 x < 2
 => (1)
 Nếu x
 Do đó ) -2x + 1 < x + 1 
	 	x > 0
=> 0< x < (2)
	 Kết hợp (1 )và (2) Ta được 0 < x < 2
 Câu4: (1,5đ)
 a) S= (0,75đ) b) S =(0,75đ)
 Câu 5 :(2đ)
 Gọi quãng đường AB là x km (x>0) 0,25đ
 Lập được phương trình 1đ
 Giải phương trình x=60 0,5đ 
 Kl: quãng đường AB dài 60 km 0,25đ
 Câu6: (3đ)
a/ Xột AMN và ABC cú:
 chung.
Do đú: AMN ABC ( c.g.c) 1đ
b/ Theo cõu a ta cú AMN ABC 
hay 
 MN = 4cm. 1đ
c/ Gọi H là trung điểm của BE.
HG là đường trung bỡnh của BED nờn HG // BD và HG = .
TT: HF // EC và HF = .
Vỡ BD = EC do đú HG = HF HFG cõn tại H 
Suy ra 
Nờn APQ cõn tại A. 1đ