Bài tập ôn tập Hình học Lớp 8 - Chuyển góc trên đường tròn
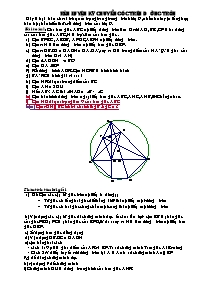
Bài toán 1: Cho tam giác ABC nội tiếp đờng tròn tâm O với AD , BE ,CF là ba đờng cao của tam giác ABC ,H là trực tâm của tam giác .
a) C/m BFEC , AEDB , AFDC, AEFH nội tiếp đờng tròn .
b) C/mr: H là tâm đờng tròn nội tiếp tam giác DEF .
c) C/mr: DB.CD = DA.DH = DA.DA’, suy ra D là trung điểm của HA’(A’ là giao của đờng tròn O và AH )
d) C/m 4AD.DH BC2
e) C/m OA EF
f) Kẻ đờng kính AOK .C/m HCKB là hình bình hành
g) BA’KC là hình gì ? vì sao ?
h) C/m HK đi qua trung điểm của BC
i) C/m AH = 2OM
j) Nếu AB < ac="" thì="" hao="B" -="" c="">
k) C/m bán kính đờng tròn ngoại tiếp tam giác ABC ,AHC,AHB,BHC bằng nhau.
l) C/m HO đi qua trọng tâm G của tam giác ABC
m) C/mr OH // BC khi và chỉ khi tagB .tagC = 3
Bạn đang xem 20 trang mẫu của tài liệu "Bài tập ôn tập Hình học Lớp 8 - Chuyển góc trên đường tròn", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Rèn luyện kỹ chuyển góc trên đường tròn Đây là loại toán có vai trò quan trọng trong trương trình lớp 9 ,nhằm ôn luyện tổng hợp toàn bộ phần kiến thức về đường tròn của lớp 9 . Bài toán 1: Cho tam giác ABC nội tiếp đường tròn tâm O với AD , BE ,CF là ba đường cao của tam giác ABC ,H là trực tâm của tam giác . C/m BFEC , AEDB , AFDC, AEFH nội tiếp đường tròn . C/mr: H là tâm đường tròn nội tiếp tam giác DEF . C/mr: DB.CD = DA.DH = DA.DA’, suy ra D là trung điểm của HA’(A’ là giao của đường tròn O và AH ) C/m 4AD.DH BC2 C/m OA EF Kẻ đường kính AOK .C/m HCKB là hình bình hành BA’KC là hình gì ? vì sao ? C/m HK đi qua trung điểm của BC C/m AH = 2OM Nếu AB < AC thì HAO = B - C C/m bán kính đường tròn ngoại tiếp tam giác ABC ,AHC,AHB,BHC bằng nhau. C/m HO đi qua trọng tâm G của tam giác ABC C/mr OH // BC khi và chỉ khi tagB .tagC = 3 Phân tích tìm lời giải Để C/m các cặp tứ giác trên nội tiếp ta dùng pp Tứ giác có tổng hai góc đối bằng 1800 thì nội tiếp một đường tròn Tứ giác có hai góc cùng chắn một cung thì nội tiếp một đường tròn b)Vận dụng các cặp tứ giác đã chứng minh được ở câu a lần lượt c/m EB là phân giác của góc FED ; FC là phân giác của EFD ,từ đo ssuy ra H là tâm đường tròn nội tiếp tam giác DEF . c) Sử dụng tam giác đồng dạng d) Vận dụng DB.DC = DA.DH e)c/m bằng hai cách - cách 1: Gọi I là giao điểm của AK và EF .Ta sẽ chứng minh Tam giác AIE vuông - Cách 2: Vẽ tiếp tuyến với đường tròn tại A là Ax ta sẽ chứng minh Ax // EF f ,g dễ dàng chứng minh được h) vận dụng f để chứng minh i)Chứng minh OM là đường trung bình của tam giác AHK j)Cần để ý cung BA’ bằng cung CK từ đó suy ra BAH = OAC và OAC=900- AKC mà AKC = B Vì BKCH là hình bình hành nên tam giác BHC và CKB bằng nhau ,do đó bán kính đường tròn của hai tam giác này bằng nhau .C/m tương tự các trường hợp còn lại Bài toán 2: Cho hai đường tròn (O;R) và (O’:R’) cắt nhau tại C,D .M là một điểm cố định trên tia đối của tia DC ,vẽ tiếp tuyến MA đến đường tròn O ; MB đến đường tròn O’ . Từ M vẽ cát tuyến MEF đến (O) ( E nằm giữa M,F) . C/m MD .MC = MA2 = OM2 – R2 C/m MA = MB MB2= ME.MF Vẽ HK là tiếp tuyến chung của hai đường tròn (O) và (O’) ( H thuộc (O) ; K thuộc (O’) ). C/m DC đi qua trung điểm của HK Vẽ tia Dx nằm trên nửa mặt phẳng bờ là DC có chứa điểm B sao cho CDx= CAD . C/m Dx là tiếp tuyến của (O) . f)C/m ID + IC DC ( I là trung điểm của HK) Phân tích tìm lời giải: Dễ dàng C/m được Cần để ý rằng MCD là cát tuyến chung của hai đường tròn C/m ME .MF = MD .MC từ đó suy ra điều phải c/m Gọi I là giao điểm của HK và CD ta sẽ chứng minh I là trung điểm của HK Vận dụng góc tạo bởi tt và dây cung áp dụng BĐT Cô Si Bài toán 3: Cho hình vuông ABCD có cạnh bằng a . Các điểm M,N lần lượt di động trên cạnh ADB,CD sao cho MBN = 450 ,AC cắt BM,BN lần lượt tại E,F . C/m A,B,F,M cùng một đường tròn C/m B,C,N,E cùng thuộc một đường tròn C/m M,E,F,N cùng thuộc một đường tròn Gọi H là giao của NE ,MF .C/m BH MN C/m MN tiếp xúc với một đường tròn cố định . Xác định tâm và bán kính của đường tròn đó C/m DM + DN + MN = 2a . Tìm vị trí của điểm M,N trên AD ;CD để diện tích tam giác DMN lớn nhất . Phân tích tìm lời giải : Để C/m a,b,c ta vận dụng cách chứng minh tứ giác nội tiếp d) Vận dụng tính chất đồng quy của ba đường cao trong tam giác C/m AB = BI = BC Vận dụng tính chất hai tt cắt nhau Bài toán 43: Cho đường tròn (O;R) đk AB , C là một điểm trên đường kính AB . Trên đường tròn lấy điểm D và M là trung điểm của cung BD , MC cắt đường tròn tại E , DE cắt AM tại K . Vẽ đường thẳng qua C song song với AD và cắt DE tại F . C/m : Tứ giác AKCE nội tiếp CK // BD C,B,E,F cùng thuộc một đường tròn CF = CB . Phân tích tìm lời giải : Chứng minh cung DM bằng cung MB C/m CK // BD ta sẽ chưng minh KCA = AEK = AED = B Chứng minh EFC = ABE suy ra CBFE nội tiếp Muốn chứng minh CF = CB ta sẽ chứng minh tam giác CFB cân tại C Bài toán 54: Cho đường tròn tâm (O;R) Và hai đường kính AB ,CD vuông góc với nhau . E là một điểm trên cung AD ,EC cắt AB tại M . a)C/m E,M,O,D thuộc một đường tròn b)Tính EA2 + EB2 + EC2 + ED2 ; CM . EC theo R c) C/m EM là phân giác của góc AEB d) C/m MA . MB = CM .EM e) f) Chứng minh ED = 2EK , EC = 3ED khi CM đi qua trung điểm của AD Phân tích tìm lời giải Muốn chứng minh EMOD thuộc một đường tròn ta sẽ chứng minh E + O = 1800 áp dụng định lí PyTago trong các tam giác AEB ; DEC ; vận dụng tính chất tiếp tuyến tính CM. EC Để chứng minh EM là phân giác của AEB ta chỉ cần chứng minh góc AEC = CEB Muốn chứng minh MA.MB = CM . ME dựa vào tam giác đồng dạng Sử dụng phương pháp diện tích SMAE + SMEB = SAEB Để c/m ED = 2EK ; EC = 3DE ta tính ED EK theo R và tính EC theo R Bài toán 65: Tính Cho ba điểm A,B,C thẳng hàng theo thứ tự đó ,đường thẳng d vuông góc với AB tại C . Điểm M di động trên đường thẳng d ,vẽ BD AM tại D ,BD cắt d tại N . AN và BM cắt nhau tại E . C/m CM. CN không đổi C/m đường tròn đường kính MN đi qua hai điểm cố định Chứng minh đường tròn ngoại tiếp tam giác AMN đi qua hai điểm cố định C/m tâm đường tròn ngoại tiếp tam giác AMN thuộc một đường cố định C/m đường trung trực của DE đi qua một điểm cố định Gọi P;Q là giao điểm của DE và đường tròn ngoại tiếp tam giác AMN .Vẽ đường kính AF của đường tròn ngoại tiếp tam giác AMN . DE cắt AF tại I 1)Tứ giác BMFN là hình gì ? vì sao ? 2)C/m AF DE 3)C/m AP2 = AQ2 = AF .AI 4) C/m P di động trên một đường cố định Phương pháp dậy bài toán này : Trong mỗi câu hỏi trong bài là tính chất hay cho nên cấn khai thác từ bài toán này thành các bài toán nhỏ và cần chốt phương pháp . Bài toán 76: (Dành cho học sinh khá - giỏi ) Cho hai đường tròn tâm (O) và (O’) ngoài nhau .Kẻ các tiếp tuyến chung ngoài AB và A’B’, các tiếp tuyến chung trong CD và EF ( A,A’,C,E (O) ; B,B’ , D,E (O’) ) .Gọi M là giao điểm của AB và EF ,N là giao điểm của A’B’ và CD . H là giao điểm của MN và OO’ . Chứng minh rằng : C/m MN OO’ Năm điểm O’, B, M,H,F cùng thuộc một đường tròn Năm điểm O,A,M,E,H thuộc một đường tròn Ba điểm H,B,D thẳng hàng e) CD = EF f) A,H ,C thẳng hàng Hướng dẫn : Do tính chất đối xứng qua OO’ nên MN OO’ Năm điểm cùng thuộc đường tròn có đường kính O’M Năm điểm cùng thuộc đường tròn có đường kính OM Do tính đối xứng nên O’HD = O’HF .Do câu b ta có O’HB = O’HF . Vậy O’HD = O’HB ,suy ra H,B,D thẳng hàng Do tính đối xứng nên CHN = EHM Do câu c ta có EHM = AHM .Suy ra CHN = AHM .Dễ dàng chứng minh A,H,C thẳng hàng f) Sử dụng tính chất tiếp tuyến Bài toán 8: Cho tam tam giác ABC vuông cân tại A có AB = AC a , trung tuyến AD . M là một điểm di động trên đoạn AD . Gọi N,P lần lượt là hình chiếu vuông góc của M trên cạnh AB, AC . PD cắt tia Bx vuông góc với AB ở điểm E . Gọi H là hình chiếu của điểm N trên trên PD . Tứ giác APMN là hình gì ? tại sao ? C/m: 5 điểm A,P,H,M,N cùng thuộc một đường tròn C/m Tứ giác BNHE nội tiếp C/m B,M,H thẳng hàng Xác định vị trí điểm M để tam giác AHB có diện tích lớn nhất .Tính giá trị lớn nhất đó theo a . Chứng tỏ khi M c/đ trên AD thì HN luôn đi qua một điểm cố định . Tìm vị trí của điểm M để HN lớn nhất . Phân tích tìm lời giải APMN là hình vuông 5 điểm A,P,M,NH cùng thuộc đường tròn đường kính PN,AM . Ta có suy ra BNHE nội tiếp ,do đó BH vuông góc với AH(1) (chú ý do đó suy ra ) Do MH vuông góc AH (2) Từ (1) và (2) suy ra B,M,H thẳng hàng Ta có SAHB = AH.BH = AH2 HB2 = Dờu bằng xảy ra khi HB = HA khi và chỉ khi H trùng D .Lúc đó M trung D Ta thấy H nằm trên đường tròn đường kính AB và HN là tia phân giác của góc AHB từ đó suy ra HN đi qua trung điểm của nửa đường tròn đường kính AB . Để HN lớn nhất khi M trùng D . Các bài tập vận dụng Bài 1: Cho hình vuông ABCD . M là điểm thay đổi trên cạnh BC ( M không trung với B) và N là điểm thay đổi trên cạnh CD ( N không trung D )sao cho MAN = MAB +NAD BD cắt AN, AM tương ướng tại P,Q . Chứng minh 5 điểm P, Q,M,C,N cùng nằm trên một đường tròn . C/m MN luôn tiếp xúc với một đường cố định khi m,n thay đổi Ký hiệu dt(APQ) = S1 , dt(PQMN) = S2 . Chứng minh không đổi khi m,n thay đổi Bài 2: Cho đoạn thẳng AB cố định ; đường thẳng vuông góc với AB tại H (HA > HB) và H ở ngoài đoạn AB . M di động trên d , C là hình chiếu của B trên AM , BC cắt d tại N ,AN cắt BM tại D . C/m đường tròn đường kính MN luôn đi qua hai điểm cố định ,gọi là I ;J C/m tâm đường tròn ngoại tiếp tam giác AMN thuộc một đường cố định C/m CD đi qua một điểm cố định Bài 3: Cho (C) đường kính BC = 2R và điểm A thay đổi trên (C) ( A không trùng với B,C) . Đường phân giác góc A của tam tam giác ABC cắt đường tròn (C) tại điểm K ( K khác A) .Hạ AH BC . Đặt AH = x . Tính diện tích S của tam giác AHK theo R và x .Tìm x sao cho S đạt GTLN C/mr khi A thay đổi ,tổng AH2 + AK2 luôn không đổi Tính góc B của tam giác ABC biết rằng Bài 4: Cho tam giác ABC có các góc nhọn , các đường cao AD ; BE ;CF cắt nhau tại H . Gọi I,K thứ tự là hình chiếu của BC trên EF . Điểm H có vị trí như thế nào đối với tam giác DEF Chứng minh DE + DF = EF Bài 5: Cho nửa đường tròn tâm O đường kính AB = 2R . Gọi C là điểm chính giữa của cung AB .Trên bán kính OC lấy điểm E .Đường thẳng AE cắt nửa đường tròn O tại F . C/m AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CEF Đường thẳng BF cắt đường thẳng CO tại K . Gọi P là giao điểm thứ hai của đường thẳng AE với đường tròn ngoại tiếp tam giác BEK .Khi E di động trên OC thì P di động trên đường nào ? Trường hợp đường thẳng AE đi qua trung điểm I của BC .Tính diện tích của hình tròn ngoại tiếp tam giác CEF theo R . Bài 6: Cho đường tròn tâm O ,các tiếp tuyến với đường tròn tại B,C cắt nhau tại A tạo thành góc BAC bằng 600 .Gọi M là điểm thuộc cung nhỏ BC ,tiếp tuyến của đường tròn tại M cắt AB; AC theo thứ tự ở D, E . Gọi giao điểm của OD ;OE với BC theo thứ tự tại I,K . C/m OM, DK , EI đồng quy So sánh độ dài IK và DE Bài 7: Cho nửa đường tròn tâm O ,đường kính BC và một điểm A trên nửa đường tròn ( Akhác B,C) . Hạ AH BC ( H thuộc BC) . Trên nửa mặt phẳng bờ là BC không chứa A dựng hai nửa đường tròn có đường kính lần lượt là BH, CH Chúng lần lượt cắt AB, AC tại E,F . C/m AE . AB = AF .AC Chứng minh EF là tiếp tuyến chung của hai nửa đường tròn đường kính BH , CH Gọi I,K lần lượt là hai điểm đối xứng với H qua AB;AC .C/m I,A,K thẳng hàng Đường thẳng IK cắt tiếp tuyến kẻ từ B với nửa đường tròn (O) tại M . Chứng minh rằng MC ; EF AH đồng quy Bài 8: Cho A là một điểm bất kỳ trên nửa đường tròn đường kính BC ( A khac B,C) .Hạ AH BC tại H .Gọi I,K lần lượt là tâm đường tròn nội tiếp tam giác AHB; AHC . Đường thẳng IK cắt cạnh AB , AC lần lượt tại M;N. ... số đo cung AB và độ dài AC 2/ Từ A vẽ đường thẳng vuông góc với BC tại D . Tính độ dài AD , BD , BC theo R 3/ Khi M c/đ trên cung lớn AC ; Chứng tở tâm đường tròn nội tiếp tam giác MAC di động trên đường cố định có giới hạn .(HD: Tính góc AIC bằng 1200) Bài 65: Cho đường tròn tâm O cố định , BC là một dây cung cố định của đường tròn (O) , A là điểm di động trên cung lớn BC sao cho tam giác ABC luôn có ba góc nhọn . BB’; CC’ là hai đường cao của tam giác ABC . 1/ C/m bôn điểm B, C’ , B’ ,C cùng thuộc một đường tròn 2/ C/m : AB AC’ = AC AB’ 3/ M là điểm chính giữa cung nhỏ BC của BC của đường tròn (O) . Tìm tập hợp trung điểm N của AM khi A di động . Bài 66 : Cho tâm giác ABC đều nội tiếp đường tròn tâm (O ,R) gọi AI là một đường kính cố định và D là điểm di động trên cung nhỏ AC ( D khác A,C ) . 1/ Tính cạnh của tam giác ABC theo R và C/m Ai là phân giác của góc BAC . 2/ Trên tia DB lấy đoạn DE = DC , chứng tỏ tam giác CDE đều và DI CE 3/ Suy ra E di dộng trên đường tròn mà phải xác định tâm và giới hạn . 4/ Tính theo R dt tam giác ADI lúc D là điểm chính giữa cung AC . Bài 67 : Cho tam giác cân ABC nội tiếp trong đường tròn (O,R) có AB = AC = 1/ Tính độ dài các cạnh của tam giác ABC theo R 2/ M là một điểm di động trên cung nhỏ AC , đường thẳng AM cắt đường thẳng BC tại D . Chứng tỏ tích AM AD luôn luôn là hằng số . 3/ Chứng tỏ tâm đường tròn ngoại tiếp tam giác MCD di động trên đường thẳng cố định khi M chuyển động trên cung nhỏ AC . 4/ C/m : AD2- AC BD = 2R2 5/ C/m AC là tt của đường tròn ngoại tiếp tam giác MDC. Bài 68 : Cho đường tròn (O,R) và điểm A sao cho OA = , một đường thẩng d quay quanh A cắt (O) tại M,N ; gọi I là trung điểm của đoạn MN . 1/ Chứng tỏ rằng IO MN , suy ra I chuyển động trên một cung cố định với hai điểm giới hạn B,C thuộc đường tròn (O) . 2/ Tính theo R độ dài AB,AC ; suy ra A,O , B,C là bốn đỉnh của hình vuông . 3/ Tính theo Rdt phần mp giới hạn bởi đoạn AB , AC và cung nhỏ BC của đường tròn tâm O . 4/ Hãy chỉ ra vị trí của đường thẳng d tương ướng lúc tổng AM + AN lớn nhất và C/m điều ấy . Bài 70: Từ điểm A ở ngoài đường tròn (O) vẽ hai tiếp tuyến AB ; AC Gọi I là trung điểm của MN . C/m AB2 = AM .AN C/m tứ giác ABIC nội tiếp Gọi T là giao điểm của BC và AI .C/m Bài 71: Cho tam giác ABC vuông tại A ,vẽ đường cao AH .Gọi I và I’ lần lượt là tâm đường tròn nội tiếp tam giácÂBH ,ACH .Đường thẳng II’ cắt AB ,AC lần lượt tại J,J’ C/m: Tam giác HIA và HI’C đồng dạng Gọi O là tâm đường tròn nội tiếp tam giác ABC C/m: C/m : AJ = AJ’ C/m : HI’J’C ; HIJB nội tiếp được trong đường tròn C/m : IJ’ = HI + HI’ + II’ Gọi r ; r1 ;r2 lần lượt là bán kính đường tròn nội tiếp tam giác ABC ; AHB ;AHC. C/m: 2r = AB + AC – BC AH = r + r1 + r2 r2 = r21+r22 Bài 72: Cho tam giác ABC nhọn ,trực tâm H .Lấy điểm K đối xứng với H qua BC . C/m tứ giác ABKC nội tiếp Cho M là điểm chuyển động trên cung nhỏ AC .C/m trung điểm I của KM chạy trên một cung tròn cố định Gọi E,F thứ tự là hình chiếu của M trên AB,AC .Chứng minh rằng EF đi qua trung điểm của MH . Bài 73: Cho đoạn thẳng AB = 2a có O là trung điểm .Trên cùng nửa mặt phẳng bờ AB vãe nửa đường tròn đường kính AB và nửa đường tròn (O’) đường kính AO .Trên đường tròn (O’) lấy điểm M ( khác Avà O) ,tia OM cắt đường tròn (O) tại C , gọi D là giao điểm thứ hai của CA với đường tròn (O’) . a) C/m tam giác ADM cân b) Tiếp tuyến tại C của đường tròn (O) cắt tia OD tại E ,xác định vị trí tương đối của đường thẳng EA đối với đường tròn (O) và (O’) . Đường thẳng AM cắt OD tại H ,đường tròn ngoại tiếp tam giác COH cắt đường tròn (O) tại điểm thứ hai là N .C/m ba điểm A,M,N thẳng hàng . Tìm vị trí của M sao cho ME // AB , hãy tính độ dài đoạn thẳng OM theo a . Bài 74: Cho đường tròn (O;R) và dây BC cố định (BC < 2R) và điểm A trên cung lớn BC ( A không trùng B,C ; A không phải là điểm chính giữa cung BC) .Gọi H là hình chiếu của A trên BC . E,F lần lượt là hình chiếu của B,C trên đường kính AA’. C/m : HE AC C/m : tam giác HEF và ABC đồng dạng Khi A c/đ trên đường tròn (O) .Cmr tâm đường tròn ngoại tiếo tam giác HEF cố định . (HD: Gọi I,J lần lượt là trung điểm của AB,BC ta sẽ c/m IH = IF = IE) Bài 75: Cho đường tròn (O;R) và dây BC cố định . A là điểm di động trên cung lớn BC của đường tròn O .( A khác B,C) .Tia phân giác của góc ACB căt đường tròn O tại D khác C ; lấy điểm I thuộc đoạn DCấo DI = DB .đường thẳng BI cắt đường tròn (O) tại K khác B . C/m tam giác KAC cân C/m đường thẳng AI luôn đi qua một điểm J cố định ,từ đó hãy xác định vị trí của điểm A để AI max Trên tia đối của tia AB lấy điểm M sao cho AM = AC .Tìm tập hợp các điểm M khi A di động trên cung lớn BC của đường tròn (O) . Bài 76 : Cho tam giác ABC có góc A bằng 600 , AC = b , AB = c ( b> c) .Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M . Gọi I,J lần lượt là chân đường vuông góc hạ từ E xuống AB ,AC . H,K là chân đường vuông góc hạ từ F xuống AB và AC . C/m các tứ giác AIEJ và CMJE nội tiếp được trong đường tròn C/m ba điểm M,I,J thẳng hàng và TJ vuông góc HK Tính độ dài BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b,c. Tính IH + JK theo b,c. Bài 77 :Cho đường tròn (O;R) và dây cung BC với góc BOC bằng 1200 . Các tiếp tuyến vẽ từ B,C cắt nhau tại A . Gọi M là điểm tuỳ ý trên cung nhỏ BC . Tiếp tuyến tại M với đường tròn (O) cắt AB tại E ,AC tại F . a) Tính góc EOF b) C/m tam giác ABC đều và tính chu của tam giác AEF theo R c)Gọi I,K tương ứng là giao điểm của BC với OE ,OF . C/m OIFC nội tiếp . d) C/m OM ,EK ,FI đồng quy e) C/m tam giác OIK và OFE đồng dạng f) C/m EF = 2IK Bài 78: Cho góc xOy và hai điểm A,B trên cạnh Ox ( A nằm giữa O,B) .M là một điểm tuỳ ý trên cạnh Oy .Đường tròn (T) đường kính AB cắt tia MA ,MB lần lượt tại điểm thức hai là C,E . Tia OE cắt đường tròn (T) tại điểm thứ hai F . C/m 4 điểm O,A,E,M nằm trên một đường tròn .Xác định tâm của đường tròn đó . Tứ giác OEFM là hình gì ? vì sao ? C/m OE.OF + BE .BM = OB2 Xác định vị trí điểm M để tứ giác OCFM là hình bình hành Tìm mối liên hệ giữa OA và OB để tứ giác OCFM là hình thoi . Bài 79: Cho tam giác ABC nhọn , kẻ hai đường cao BE ,CF . 1Biết góc BAC bằng 600 ,tính độ dài EF theo BC = a 2)Trên nửa đường tròn đường kính BC không chứa điểm E,F lấy điểm M bất kỳ . Gọi H,I,K lần lượt là hình chiếu vuông góc của M trên BC , CE ,EB . Tìm GTNN của Bài 80: Cho tam giác ABC nội tiếp đường tròn tâm O ,có các đường phân giác trong cắt nhau tại I . các đường thẳng AI ,BI,CI cắt đường tròn (O) tương ứng tại các điểm M,N,P C/m tam giác NIC cân C/m I là trực tâm của tam giác MNP Gọi E là giao điểm của MN và AC ; F là giao điểm của PM và AB .C/m ba điểm E,I,F thẳng hàng Gọi K là trung điểm của BC và G/s rằng BI vuông góc với IK ;BI = 2IK .Tính góc BAC . Bài 81: Cho đường tròn (O;4) dây cung BC của đường tròn (O) ( BC < 8) .Điểm A chạy trên cung lớn BC sao cho tam giác ABC nhọn . Gọi AD ,BE ,CF là các đường cao của tam giác ABC . a)C/m tứ giác BFEC nội tiếp b)C/m tam giác AEF và tam giác ABC đồng dạng c)C/m AO vuông góc với EF d) Tính độ dài BC khi diện tích tứ giác BFEC gấp ba lần diện tích tam giác AEF . Bài 82:Cho đường tròn tâm (O;R) .Đường thẳng d tiếp xúc với đường tròn O tại A .M là một điểm chạy trên đường thẳng d ( M khác A) .Kẻ tiếp tuyến MB đến đường tròn O ( B là tiếp điểm và B khác A).Gọi H là chân đường vuông góc kẻ từ B xuống d .BH cắt OM tại I . C/m AI vuông góc với MB C/m tứ giác AOBI là hình thoi Xác định vị trí điểm M trên đường thẳng d để diện tích AOBI max . Tìm quỹ tích điểm I Bài 83:Cho đường tròn tâm (O;R) và dây BC của đường tròn (O) ( BC < 2R) .D là điểm chính giữa của cung BC .Điểm A chạy trên cung lớn BC ( A khác B,C) .AD cắt BC tại E a)C/m BD là tiếp tuyến của đừơng tròn ngoại tiếp tam giác ABE b)C/m tâm đường tròn ngoại tiếp tam giác ABE chạy trên một đường cố định c) C/m : AE2 = AB .AC – EB.EC ,từ đó chứng minh AD2 d) C/m tổng bán kính hai đường tròn ngoại tiếp tam giác ABE và ACF không đổi . Bài 84: Cho đường tròn (O;R) và một điểm A ở ngoài đường tròn .Từ A kẻ hai tiếp tuyến AB ;AC với đường tròn . C/m Tứ giác ABOC nội tiếp trong đường tròn Qua B kẻ đường thẳng song với AC cắt đường tròn (O) tại D ( D khác B) .Đường thẳng AD cắt đường tròn (O) tại E .C/m:AB2 = AE.AD C/m tia đối của tia EC là phân giác của góc AEB . Đường thẳng BE cắt AC tại M chứng minh MA = MC Bài 85: Cho nửa đường tròn đường kính AB = 2R .Gọi C là điểm chính giữa cung AB .Trên cung AC lấy điểm F ( F khác A,C) .Trên tia BF lấy điểm E sao cho BE = CF . C/m tam giác AFC bằng tam giác BEC C/m Tam giác EFC vuông cân Gọi D là giao điểm của đường thẳng AC với đường vuông góc với AB tại B .C/m tứ giác BECD nội tiếp trong đường tròn Khi F chuyển động trên cung AC ( khác điểm A,C) Tìm quỹ tích điểm E Bài 86:Cho tam giác MNP ( M < 900 ) nội tiếp đường tròn tâm O ,bán kính R . Các đường cao NK ,PS cắt đường tròn (O) tương ứng tại các điểm N1; P1 C/m SK // P1N1 C/m OM vuông góc với SK C/m bán kính đường tròn ngoại tiếp tam giác MSK không đổi khi M c/đ trên cung lớn NP của đường tròn (O) Bài 87: Cho tam giác ABC nhọn nội tiếp đường tròn tâm (O) có góc A bằng 600 và ngoại tiếp đường tròn tâm (I) .Gọi H là trực tâm của tam giác ABC .Đường thẳng OH cắt cạnh AB tại M ,AC tại N . C/m 5 điểm B,H,I,O,C cùng nằm trên đường tròn C/m BM + CN = MN Gọi D,E lần lượt là các tiếp điểm của đường tròn tâm (I) với AB,BC ,AI cắt DE tại G .C/m góc AGC bằng 900 Bài 88: Cho đường tròn (O;R) và đường kính AB ,qua B vẽ tiếp tuyến xx’ với đường tròn (O) .Gọi MN là đường kính bất kỳ của đường tròn (O) .AM ,AN cắt xx’ lần lượt tại P,Q. C/m Tứ giác AMBN là hình chữ nhật C/m tư C/m tứ giác MNQP nội tiếp được trong đường tròn tính dt(MNQP) theo R ,biết góc MAB bằng 300 Khi MN không vuông góc với AB .Gọi giao điểm thứ hai của đường tròn ngoại tiếp tam giác APQ với đường tròn (O) là E .C/m MN, PQ ,AE đồng quy . Bài 89: Cho tứ giác ABCD nội tiếp trong đường tròn (O;R) có hai đường chéo AC, BD vuông góc với nhau tại I khác O. a) C/m IA.IC = IB.ID b) Vẽ đường kính DE .C/m ADBE là hình thang cân c) C/m AB2 + CD2 = 4R2 và AB2 + CD2 + BC2 + AD2 = 8R2 d) Từ A,B kẻ các đường vuông góc đến CD lần lượt cắt BD tại F ,cắt AC tại K . C/m A,B,K,F là bốn đỉnh của tứ giác đặc biệt e) Gọi M là trung điểm của CD ,C/m AB = 2OM f) Cho đường tròn (O;R) và điểm I cố định : A,B,C,D di chuyển ;gọi P là trung điểm của OI ,H là chân đường cao vẽ từ I của tam giác CID . a) C/m OM2 + MI2 – 2MP2 = OI2 /2 ,suy ra M,H cùng thuộc một đường tròn cố định tâm P b) Tìm vị trí của ABCD sao cho tam giác ICD có diện tích lớn nhất .
Tài liệu đính kèm:
 bai_tap_on_tap_hinh_hoc_lop_8_chuyen_goc_tren_duong_tron.doc
bai_tap_on_tap_hinh_hoc_lop_8_chuyen_goc_tren_duong_tron.doc





