Ma trận và đề thi học kì I Toán Lớp 8 - Năm học 2011-2012

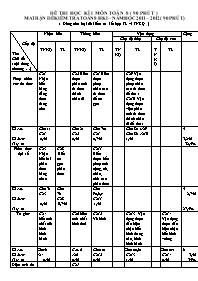
ĐỀ THI HỌC KÌ I MÔN TOÁN 8 ( 90 PHÚT )
MA TRẬN ĐỀ KIỂM TRA TOÁN 8 HKI – NĂM HỌC 2011 – 2012 ( 90 PHÚT )
( Dùng cho loại đề kiểm tra kết hợp TL và TNKQ )
 Cấp độ
Tên
Chủ đề
( nội dung chương )
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
TNKQ
TL
TNKQ
TL
TNKQ
TL
TNKQ
TL
Phép nhân các đa thức 
Ch1:
Nhận biết hằng đẳng thức đáng nhớ
Ch2:Hiểu được phân tích đa thức thành nhân tử
Ch7:Hiểu được phép nhân các đa thức để rút gọn
Ch9:Vận dụng được phép nhân các đa thức để tìm x
Ch10:Vận dụng được việc phân tích đa thức thành nhân tử để tìm x
Số câu
Số điểm
Tỉ lệ %
Câu 1:
Ch1
 0,5đ
Câu 2: Ch2 
0,5đ
Câu 7a: Ch7 
0,75đ
Câu 8a :ch9
Câu 8b ch10 1,5đ
5 
3,25đ 
 32,5% 
Phân thức đại số
Ch3:
Nhận biết hai phân thức bằng nhau
Ch8:
 Biết rút gọn phân thức
Ch11:
Hiểu được bốn phép tính cộng, trừ, nhân, chia các phân thức
Số câu
Số điểm
Tỉ lệ %
Câu 3:
Ch3
 0,5đ
Câu 7b
Ch8
 0,75đ
Câu 9a,b,c
Ch11
 1,5đ
5
2,75đ
27,5%
Tứ giác
Ch4: biết tính chất của hình bình hành
Ch6:hiểu tính chất hình thoi
Ch12
Vẽ hình
Ch13: Vận dụng được dấu hiệu nhận biết hình thang cân, hình bình hành
Ch14: Vận dụng được dấu hiệu nhận biết hình vuông
Số câu
Số điểm
Tỉ lệ %
Câu4: ch4
 0,5đ
Câu 6: ch6 0,5đ
Câu10:
Ch12
0,5đ
Câu10a,b:
Ch13 
1,5đ
Câu10c:
Ch14 
0,5đ
6
3,5đ
35%
Diện tích đa giác
Ch5:
Hiểu cách tính diện tích hình chữ nhật
Số câu
Số điểm
Tỉ lệ %
Câu 5 
 Ch5: 0,5đ
1
0,5đ
5%
Tổng số câu
Tổng số điểm
Tỉ lệ %
4
 2,25đ
 22,5%
8
4,25đ
42,5%
5
3,5đ
35%
17
10đ
100%
PHÒNG GD&ĐT LONG THÀNH	 KIỂM TRA HỌC KÌ I – LỚP 8
TRƯỜNG THCS TT LONG THÀNH	 NĂM HỌC 2011 – 2012
Môn thi : Toán
Thời gian làm bài : 90 phút
Ngày thi :27/12/2011
TRẮC NGHIỆM : ( 3 điểm ). Có tất cả 6 câu, mỗi câu trả lời đúng đạt 0,5 điểm.
Hãy chọn câu trả lời mà em cho là đúng nhất
Câu 1 : Khai triển ( x – 2 )2 được kết quả là :
a) x2 + 4x + 4 	b) x2 – 4x +4 	c) x2 – 4 	d) x2 – 4x + 2 
Câu 2 : Phân tích đa thức 2x2 – 6x thành nhân tử được kết quả là :
a) 2x( x – 3 )	b) 2x( x – 4 )	c) x( x2 – 6)	d) 2( x2 – 3 )
Câu 3: Hai phân thức gọi là bằng nhau nếu :
a) MP = NQ	b) MQ = NP	c) MN = PQ	d) Cả a), b), c) đều đúng
Câu 4: Chọn câu SAI ? 
Trong hình bình hành :
a) Hai cạnh đối bằng nhau	b) Hai góc đối bằng nhau	
c) Hai đường chéo bằng nhau 	d) Hai cạnh đối song song
Câu 5: Một hình chữ nhật có hai kích thước là 8cm và 15cm. Diện tích hình chữ nhật đó bằng :
a) 23cm2	b) 46cm2	c) 120cm2	d) 60cm2
Câu 6: Một hình thoi có hai đường chéo là 8cm và 6cm. Độ dài cạnh hình thoi đó bằng :
a) 3 cm	b) 4cm	c) 5cm 	d) 9cm
II. TỰ LUẬN : ( 7 điểm ). Có tất cả 4 câu.
Câu 7: Rút gọn các biểu thức sau :( 1.5 điểm )
( x + 3)2 + ( 4 – x )( x + 2 )
Câu 8: Tìm x, biết :( 1.5 điểm )
a) x( 3x – 2) + ( 3 – x )( 3x + 4 ) = 0
b) 6( x – 3 ) + x2 – 9 = 0
Câu 9: Thực hiện phép tính : ( 1.5 điểm )
b) 	c) 
Câu 10( 2.5 điểm ): 
Cho ΔABC cân tại A. Gọi M là trung điểm của AB. Qua M kẻ đường thẳng song song với BC, cắt AC tại N.
Chứng minh : tứ giác BMNC là hình thang cân.
b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác BMEC là hình bình hành.
c) Gọi P là trung điểm của BC. ΔABC cần có điều kiện gì để tứ giác AMPN là hình vuông ?
- HẾT –
PHÒNG GD&ĐT LONG THÀNH	 KIỂM TRA HỌC KÌ I – LỚP 8
TRƯỜNG THCS TT LONG THÀNH	 HƯỚNG DẪN CHẤM MÔN TOÁN
I. TRẮC NGHIỆM ( Mỗi câu trả lời đúng đạt 0,5 điểm )
Câu
1
2
3
4
5
6
Đáp án
b
a
b
c
c
c
TỰ LUẬN :
CÂU
ĐÁP ÁN
ĐIỂM
7a
( x + 3)2 + ( 4 – x )( x + 2 )
= x2 + 6x + 9 + 4x +8 – x2 – 2x 	
= 8x + 17	
0,5 
0,25
7b
= 	
0,75
8a
 x( 3x – 2) + ( 3 – x )( 3x + 4 ) = 0
3x2 – 2x + 9x +12 – 3x2 – 4x = 0	
3x = 12	
x = 4	
0,25
0,25
0,25
8b
 6( x – 3 ) + ( x – 3 )( x + 3 ) = 0
 ( x – 3 )( x + 9 ) = 0	
Nên x = 3 hoặc x = -9 	
0,25
0,25
0,25
9a
0,5
9b
0,5
9c
0,5
10
Hình vẽ 
0,5
10a
Chứng minh : Tứ giác BMNC là hình thang cân
Ta có : MN // BC nên tứ giác BMNC là hình thang
Mà BÂ = CÂ ( Vì êABC cân tại A )
Vậy BMNC là hình thang cân
1,0đ
0,5
0,25
0,25
10b
Chứng minh : Tứ giác BMEC là hình bình hành
Vì MA = MB ; MN // BC nên NA = NC
Do đó MN là đường trung bình của êABC
=> MN = ½ BC
Mà MN = ½ ME ( vì E đối xứng với M qua N )
Suy ra : ME = BC
Lại có : ME // BC ( vì MN // BC )
Vậy BMEC là hình bình hành
1,0đ
0,5
0,25
0,25
10c
Tìm điều kiện của êABC để AMPN là hình vuông ?
Ta có AM = NP = ½ AC
AN = MP = ½ AB
Mà AB = AC nên AM = MP = PN = AN
Do đó tứ giác AMPN là hình thoi
Hình thoi AMPN là hình vuông ó Â = 900
Khi này êABC phải là tam giác vuông cân tại A
0,5 đ
0,25
0,25