Giáo án Toán Lớp 8 - Chương trình cả năm - Năm học 2012-2013 - Phạm Phúc Đình

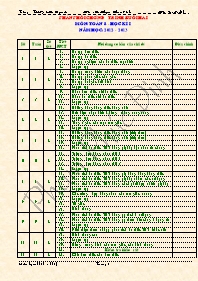
Phân phối chương trình buổi Hai
Môn: Toán 8 - Học Kì I
Năm học: 2012 - 2013
Stt
Tuần 
Số tiết
Tiết PPCT
Nội dung cơ bản của chủ đề
Điều chỉnh
1
1
4
Ôn tập đơn thức
Ôn tập đa thức
Ôn tập nghiệm của đa thức một biến
Luyện tập
2
2
4
Ôn tập trung điểm của đoạn thẳng
Ôn tập phân giác của góc
Ôn tập hai góc đối đỉnh
Luyện tập
3
3
4
Nhân đơn thức với đa thức
Nhân đa thức với đa thức
Luyện tập
Những hằng đẳng thức đáng nhớ
4
4
4
Dấu hiệu nhận biết 2 đường thẳng song song
Luyện tập
Tổng 3 góc của một tam giác
Luyện tập
5
5
4
Những hằng đẳng thức đáng nhớ (tiếp theo)
Những hằng đẳng thức đáng nhớ (tiếp theo)
Luyện tập
Phân tích đa thức TNT bằng p/pháp đặt nhân tử chung
6
6
4
Trường hợp bằng nhau thứ 1
Trường hợp bằng nhau thứ 2
Trường hợp bằng nhau thứ 3
Luyện tập
7
7
4
Phân tích đa thức TNT bằng p/p dùng hằng đẳng thức
Phân tích đa thức TNT bằng p/pháp nhóm các số hạng
Phân tích đa thức TNT bằng cách phối hợp nhiều p/pháp
Luyện tập
8
8
4
Các trường hợp bằng nhau của tam giác vuông
Luyện tập
Tứ giác
Hình thang
9
9
4
Phân tích đa thức TNT bằng pp tách 1 số hạng
Phân tích đa thức TNT bằng pp thêm bớt cùng 1 hạng tử
Luyện tập
Giới thiệu thêm vài pp phân tích đa thức TNT khác nữa
10
10
4
Hình thang cân
Luyện tập
Đường trung bình của tam giác, của hình thang
Kiểm tra khảo sát
11
11
4
Chia đơn thức cho đơn thức
Chia đa thức cho đơn thức
Chia đa thức một biến đã sắp xếp
Luyện tập
12
12
4
Hình bình hành
Luyện tập
Hình chữ nhật
Luyện tập
13
13
4
Ôn tập chương I
Luyện tập
Phân thức đại số
Tính chất cơ bản của phân thức đại số
14
14
4
Hình thoi
Luyện tập
Hình vuông
Luyện tập
15
15
4
Rút gọn phân thức đại số
Luyện tập
Quy đồng mẫu của nhiều phân thức
Luyện tập
16
16
4
Ôn tập phần tứ giác
Ôn tập phần tứ giác (tiếp theo)
Luyện tập
Kiểm tra khảo sát
17
17
4
Phép cộng các phân thức đại số
Phép trừ các phân thức đại số
Phép nhân, phép chia các phân thức đại số
Kiểm tra khảo sát
18
18
4
Diện tích hình chữ nhật
Luyện tập
Diện tích tam giác
Luyện tập
Liên Mạc, ngày 20 tháng 08 năm 2012
Người lập
 Phạm Phúc Đinh
Ngày soạn
Ngày giảng
Tiết 1: Ôn tập đơn thức
I. Mục tiêu
- HS nhận biết được biểu thức đại số nào đó là đơn thức. Nhận biết được đơn thức thu gọn. Nhận biết được phần hệ số, phần biến của đơn thức.
- HS biết nhân 2 đơn thức.
- HS biết thu gọn đơn thức.
II. Phương tiện thực hiện.
1. Giáo viên Soạn bài, bảng phụ.
2. HS Học bài, làm bài tập về nhà, bảng nhóm.
III. Cách thức tiến hành.
- Dạy học nêu và giải quyết vấn đề.
- Dạy học hợp tác trong nhóm nhỏ.
IV. Tiến trình dạy học.
A. Tổ chức:
 Sĩ số: 8A: 	8B: 
B. Kiểm tra:
- Để tính giá trị biểu thức khi biết giá trị của các biến ta làm như thế nào?
- Bài tập tính x2y3 +xy = tại x=1 và y =
C. Bài mới.
* Đơn thức.
- Đơn thức là gì?
- Số 0 có phải là đơn thức không?
- Thế nào là đơn thức thu gọn.
GV xét đơn thức 10x6y3
- Đơn thức trên có mấy biến, các biến có mặt mấy lần và dược viết dưới dạng nào?
- GV ta nói. 10x6y3 là đơn thức thu gọn?
- GV cho ví dụ về đơn thức.
- Xác định bậc của đơn thức.
- GV cho đơn thức 2x3y3z
Đơn thức trên có phải là đơn thức thu gọn không? Hãy xét phần hệ số, phần biến, số mũ của mỗi biến?
- GV Tổng các số mũ của các biến là? (9)
- Ta nói 9 là bậc của đơn thức 2x3y3z.
- HS tìm bậc của các đơn thức
GV.
+ Số thực khác không có phải là đơn thức không? Bậc là bao nhiêu?
+ Số 0 là đơn thức bậc mấy?
- Nhân hai đơn thức.
GV: Cho 2 biểu thức A = 32. 167
 B = 34. 166
Thực hiện phép tính A.B 
GV : Bằng cách tương tự ta có thể thực hiện phép nhân 2 đơn thức.
GV cho HS làm VD.
Vậy muốn nhân 2 đơn thức ta làm như thế nào?
- Thế nào là 2 đơn thức đồng dạng
GV. Để cộmg hay trừ các đơn thức đồng dạng ta làm như thế nào?
- GV cho HS làm ví dụ.
 xy2+(-2xy2) + 8xy2
1. Đơn thức:
- Đơn thức gồm 1 số, 1 biết hoặc 1 tích giữa số với các biết 
- Ví dụ: 
x2y; 9x2yz; ; y2z ; xyz
2. Đơn thức thu gọn:
VD: Đơn thức 10x6y3 là đơn thức thu gọn.
10 là hệ số.
x6y3 là phần biến.
* Khái niệm
3. Bậc của đơn thức.
- Là tổng số mũ của các biến trong đơn thức thu gọn.
Đơn thức 2x5y3z có bậc 9
 vì 5 + 3 + 1=9
VD: Tìm bậc của đơn thức.
x2y là đơn thức bậc 3.
2,5x2y là đơn thức bậc 3.
9x2yz là đơn thức bậc 4.
x6y6 là đơn thức bậc 12.
4. Nhân hai đơn thức.
Ta nhân hễ số với hệ số nhân phần biến với phần biến
Ví dụ: A = 32. 167
 B = 34. 166
A.B =( 32.167 )(34.166)
 =(32.34)(167.166) = 36.1613
VD; 2x2y .9xy4= 2.9(x2.x3)(y.y4)
 = 18x3y5
5. Đơn thức đồng dạng
Là 2 đơn thức có hệ số khác và giống nhau ở phần biến
Ví dụ xy3; 5xy3 ; -7xy3 là đồng dạng
6. Cộng trừ các đơn thức đồng dạng
- Để cộng, trừ các đơn thức đồng dạng ta cộng trừ các hệ số với nhau và giữ nguyên phần biến.
- Ví dụ.
a. xy2+(-2xy2)+8xy2 = (1-2+8)xy2 =7xy2
b. 5ab -7ab -4ab = (5-7-4)ab = - 6ab.
D. Củng cố:
- GV hệ thống lại các kiến thức cần nhớ trong bài.
- Làm bài tập 
+ Bài 1 Tính 25xy2 +55xy2 +75xy2 = ?
 	+ Bài 2 Tính giá trị biểu thức. x5y +x5y với x = 1 , y = - 1 theo 2 cách
Cách 1. Thay x =1; y = -1 vào biểu thức ta có.n.15.(-1).15(-1)+15(-1) = .
Cách 2. = ( thay x=1; y= -1 vào biểu thức x5y
Ta có. 
E. HDVN:
- HS học bài theo vở ghi và làm bài tập tính
a) xyz2+ xyz2+(- xyz2) = ?	c) x2y(-xy4) = ?
b) x4y2.xy= ? 	d) 5xy. 5x2yz = ?
- Học trước bài “ Đa thức’’
----------------------------------------------------------
Tiết 2: Ôn tập đa thứcNgày soạn:
Ngày giảng:
I. Mục tiêu.
- HS nhận biết được đa thức, cộng trừ đa thức 1 biến thông qua 1 số ví dụ cụ thể.
- Biết thu gọn đa thức, tìm bậc của đa thức.
- Có thái độ rõ ràng trong học tập
II. Phương tiện thực hiện.
1. GV: - SGK, SGV, Bảng phụ.
2. HS: - Học bài+làm bài tập về nhà +bảng nhóm.
III. Cách thức tiến hành.
- Dạy học nêu và giải quyết vấn đề.
IV. Tiến trình dạy học.
A. Tổ chức:
 Sĩ số: 8A: 	8B: 
B. Kiểm tra:
- Nêu khái niệm đơn thức, cho 3 ví dụ về đơn thức.
- Viết tổng của các đơn thức đó.
C. Bài mới.
- Khái niệm đa thức.
- GV Cho các đơn thức x2y; xy2; xy; 5. Em hãy lập tổng các đơn thức đó.
- Các bài tập trên gọi là đa thức, vậy thế nào là đa thức.
GV Nêu khái niệm đa thức, hạng tử của đa thức.
- HS chỉ rõ các hạng tử của đa thức ở phần a, b, c.
- Thu gọn đa thức.
- Em có nhận xét gì về các hạng tử của đa thức a, b, c. ở mục 1.
- Kí hiệu đa thức c, là N.
Em hãy thực hiện phép cộng các đơn thức đồng dạng trong đa thức N.
- Trong đa thức 4x2y -2xy- x+2 còn hạng tử nào đồng dạng với nhau không => đó là dạng thu gọn của đa thức N.
- GV cho HS làm
- Tìm bậc của các hạng tử trong đa thức: 
M= x2y5 –xy4 +y6+1
Hỏi hạng tử nào có bậc cao nhất?
GV cho Q = -x3y-xy2+2
Tìm bậc của đa thức Q(x)
Bài tập Thu gọn rồi tìm bậc của 2 đa thức sau
a. 3x2-x+1+2x-x2 = 2x2+x+1 ; có bậc 2.
b. 3x2+7x3-3x3+6x3-3x2=10 ; có bậc 3
Cộng 2 đa thức.
GV Yêu cầu học đọc đề bài gọi hs lên bảng trình bày.
- GV yêu cầu học sinh giải thích các bước làm.
- GV cho 2 đa thức P,Q Học sinh tính P+Q
HĐ2. Trừ 2 đa thức.
- GV gọi 2 HS làm.
- GV gới thiệu cách trừ 2 đa thức P-Q
GV gọi 2 HS lên bảng làm
 GV lưu ý HS khi bỏ dấu ngoặc đằng trước có dấu (-)
1. Đa thức.
a. x2 + y2 +xy
b. x2y + xy2+ xy +5
c. x2y -3xy +3x2y -3 +xy - x+ 5
* Khái niệm: Đa thức là tổng của các đơn thức
- Kí hiệu đa thức bằng các chữ cái in hoa.
2. Thu gọn đa thức;
N = x2y -3xy +3x2y -3 +xy - x+ 5
 = (x2y +3x2y) + (-3xy +xy) + (-3+5)
 = 4x2y -2xy -x+2
M = 5x2y- 3xy +x2y - xy +5xy -x + +x -
 = 
Để cộng trừ đa thức ta cộng trừ các số hạng đồng dạng với nhau.
3. Bậc của đa thức.
VD: Cho đa thức
M= x2y5 –xy4 +y6+1
Hạng tử x2y5 có bậc 7.
Hạng tử xy4 có bậc 5.
Hạng tử y6 có bậc 6.
Hạng tử 1 có bậc 0.
Đa thức M có bậc 7.
Q =-3x5-x3xy2+5x5+3 = -x3y-xy2+2
Q có bậc 4
4. Cộng 2 đa thức.
Ví dụ 1. M = 5x2y+ 5x -3
 N = xyz – 4x2y + 5x -
M+N = (5x2y + 5x -3)+( xyz – 4x2y + 5x -)
 = 5x2y + 5x -3+ xyz- 4x2y + 5x -
 = (5x2y- 4x2y)+ (5x +5x)+ xyz+(-3-)
 = x2y+ 10x +xyz -3 .
VD2: P = x2y+x3 –xy2 +3
 Q = x3+ xy2-xy-6
 P+Q = 2x3 + x2y-xy-3
5. Trừ 2 đa thức:
P = 5 x2y- 4xy2 +5x -3
Q = xyz -4xy2+xy2+5x-
P - Q = (5x2y - 4xy2+5x -3)-(xyz - 4x2y+ xy2+5x-)
= 5x2y - 4xy2+5x -3- xyz + 4x2y- xy2-5x+
= 9x2y-5xy2-xyz-2
D. Củng cố: - Tổng kết kiết thức cần nhớ cho HS
- HS làm bài tập sau theo từng nhóm 
Bài 1 : Cho P = x2y+xy2-xy+xy2-5xy-x2y Tính P khi x =0,5; y =1
Bài 2 Cho A(x) = x5+2x4-3x2 4x +1-x và B(x) = x5+5x4 + 2x2 - 3x +1-x
a. Hãy viết A(x) thành tổng của 2 đa thức trong đó có 1 đa thức bậc 5 và 1 đa thức bậc 1
b. Hãy viết B(x) thành tổng của 2 đa thức trong đó có 1 đa thức bậc 5 và 1 đa thức bậc 4
E. HDVN:
- HS học bài cũ ở nhà và làm bài tập
- Bài 1: Cho 2 đa thức. M=3xyz - 3x2+5xy-1 và N = 5x2+xyz-5xy+3-y Tính. M+N, M-N.
- Bài 2: A(x) = (x2-2y+xy+1)
 Tìm đa thức B(x) biết: A(x)+B(x) = x2-2y+xy+1+x2 +y-x2y2-1
------------------------------------------------------------
Tiết 3: Ôn tập nghiệm của đa thứcNgày soạn:
Ngày giảng:
 1 biến
I. Mục tiêu.
- HS hiểu được khái niệm nghiệm của đa thức, biết cách cộng trừ 2 đa thức 1 biến.
- HS biết cách kiểm tra xem số a có phải là n0 của đa thức hay không?
- HS biết 1đa thức( đa thức 0) có thể không có nghiệm, có1, 2 nghiệm, số nghiệm của 1đa thức không vượt quá bậc của nó.
II. Phương tiện thực hiện.
1. GV. Bài soạn, sgk, sbt.
2. HS. Ôn tập qui tắc chuyển vế.
III. Cách thức tiến hành.
- Dạy học nêu và giải quyết vấn đề.
- Dạy học hợp tác trong nhóm nhỏ.
IV. Tiến trình dạy học.
A. Tổ chức:
 Sĩ số: 8A: 	8B: 
B. Kiểm tra:
- Tính f(x) – g(x) biết.
f(x) =x7-3x2-x5+x4-x2+2x-7
g(x) = x- 2x2+x4-x5-2x7-4x2-1
h(x) = f(x)-g(x) = 3x7+2x2+x-6
GV. Yêu cầu học sinh tìm h(1)
 h(1) = 317+212+1-6 = 0
GV. Khi đó x = 1 gọi là n0 của đa thức h(x)
C. Bài mới.
- Cộng 2 đa thức một biến.
GV gới thiệu từ phần kiểm tra bài cũ. Đây là một cách để cộng 2 đa thức 1 biến.
- GV ngoài cách làm trên ta có thể cộng 2 đa thức theo cột dọc.
( Chú ý 2 đa thức đã được thu gọn, sắp xếp, các đơn thức đồng dạng ở cùng 1 cột)
- Trừ 2 đa thức 1 biến.
GV giới thiệu cách trình bày khác của cách 2.
- 2 HS lên bảng.
GV dẫn dắt nghiệm của đa thức một biến.
- Xét P(x)= x-
P(x)=0 khi nào?
GV giới thiệu x=32 là n0 của đa thức P(x).
- Vậy khi nào số a là n0 của đa thức P(x)
- GV nêu ví dụ.
Cho đa thức P(x)= 2x+1
 x= - có phải là n0 của đa thức P(x) không?
- Muốn xem 1số có phải là n0 của 1đa thức không , ta làm như thế nào?
- Tìm n0 của đa thức.
 Q(x) =x2-1
 G(x) =x2+1
- GV yêu cầu HS làm 
- GV. Làm thế nào để biết trong các số đã cho số nào là n0 của đa thức.
- Ngoài cách này ra còn cách nào làm khác không? (cho P(x)=0 rồi tìm x)
- Ngoài 2n0 này ra Q(x) còn n0 nào khác không? vì sao?
1. Cộng 2 đa thức một b ... ình thang, hình bình hành các tính chất của diện tích.
- Hiểu được để chứng minh các công thức đó cần phải vận dụng các tính chất của diện tích 
- Kỹ năng: Vận dụng công thức và tính chất của diện tích để giải bài toán về diện tích
- Biết cách vẽ hình chữ nhật hay hình bình hành có diện tích bằng diện tích hình bình hành cho trước.
- HS có kỹ năng vẽ hình - Làm quen với phương pháp đặc biệt hoá
- Thái độ: Kiên trì trong suy luận, cẩn thận, chính xác trong hình vẽ.
II- phương tiện thực hiện:
- GV: Bảng phụ, dụng cụ vẽ.
- HS: Thứơc com pa, đo độ, ê ke.
III. Cách thức tiến hành:
- Dạy học đặt và giải quyết vấn đề
IV- Tiến trình bài dạy
A - Tổ chức:
Lớp 8A: 	8B: 
B - Kiểm tra:
	Viết các công thức tính diện tích đã học
C - Bài mới
Hoạt động của GV và HS
Nội dung ghi bảng
+ Tạo thành hình chữ nhật
 SADC =
 S ABC =
 SABDC = 
 b
 A B
 h
 D H a E C
- GV cho HS phát biểu công thức tính diện tích hình thang?
2) Công thức tính diện tích hình bình hành
- HS phát biểu công thức.
1) Công thức tính diện tích hình thang.
 b
 A B
 h
 D H a C 
- áp dụng công thức tính diện tích tam giác ta có:
 SADC = AH. HD (1)
 S ABC = AH. AB (2)
- Theo tính chất diện tích đa giác thì :
 SABDC = S ADC + SABC
 SABDC = AH. HD + AH. AB =
 = AH.(DC + AB)
Công thức: ( sgk)
2) Công thức tính diện tích hình bình hành
.* Định lý:
- Diện tích hình bình hành bằng tích của 1cạnh nhân với chiều cao tương ứng.
S = a.h
h
 a
D - Củng cố:
	- Làm bài tập 32 SBT/ 161
	- Cho hình chữ nhật ABCD có AB =5 cm, BC = 3 cm, Vẽ hình bình hành ABEF có cạnh AB= 5 cm và có diện tích bằng diện tích của HCN ABCD, Vẽ được bao nhiêu hình bình hành ABEF như vậy?
E - Hướng dẫn về nhà
- Làm các bài tập: 34 đến 41/ SBT
----------------------------------------------------- 
Ngày soan:
Ngày giảng:
Tiết 14: Luyện tập
I- Mục tiêu:
- Kiến thức: HS nắm vững công thức tính diện tích hình thang, hình bình hành. Hiểu được để chứng minh định lý về diện tích hình thoi
- Kỹ năng: Vận dụng công thức và tính chất của diện tích để tính diện tích hình thoi.
- Biết cách vẽ hình chữ nhật hay hình bình hành có diện tích bằng diện tích hình bình hành cho trước.
- Thái độ: Kiên trì trong suy luận, cẩn thận, chính xác trong hình vẽ.
 - Tư duy nhanh, tìm tòi sáng tạo.
II- phương tiện thực hiện:
- GV: Bảng phụ, dụng cụ vẽ
- HS: Thứơc com pa, đo độ, ê ke.
III. cách thức tiến hành: 
- Luyện giải bài tập
IV- Tiến trình bài dạy
A- Tổ chức:
Lớp 8A: 	8B:
B- Kiểm tra:
- Phát biểu định lý và viết công thức tính diện tích của hình đã học?
C- Bài mới
Hoạt động của GV và HS
Nội dung ghi bang
* ễn tập lớ thuyết:
- GV chốt lại cụng thức tớnh diện tớch cỏc hỡnh đó học.
* Luyện tập:
- Cho HS làm bài tập 41( SGK trang 132)
- HS quan sỏt hỡnh vẽ và làm BT:
- Tớnh diện tớch tam giỏc DBE;
- Tớnh diện tớch tứ giỏc EHIK
HS làm bài cỏ nhõn
GV gọi một HS lờn giải bài tập
GV: Yờu cầu học sinh làm bài tập 35
-Học sinh đọc đề bài 35
- ABD là tam giỏc gỡ?
Kẻ AH vuụng gúc với AD ta suy ra điều gỡ?
HS: AH = HD, tớnh được BH theo Pytago
GV: Diện tớch hỡnh thoi ABCD tớnh như thế nào?
- HS: bằng 2 lần SABD.
- Yờu cầu 1 Hs lờn bảng trỡnh bày bài làm
+Gv nhận xột, kết luận lời giải bài toỏn
GV hướng dẫn cỏch 2. 
GV cho HS đọc đề bài 42 SGK
GV gợi ý cỏch giải: Bài toỏn đó cho những dữ kiện nào? Cần tớnh gỡ?
HS: trả lời 
GV: Tứ giỏc ABCD bao gồm những hỡnh nào ghộp lại?
HS: Tam giỏc ABC và tam giỏc ADC
GV: Tam giỏc ABC cú diện tớch bằng diện tớch tam giỏc nào? Vỡ sao?
HS:
GV gọi một HS lờn chữa bài
Lớp làm bài vào vở nhỏp
GV cho lớp nhận xột bài và KL chung
I. Lý thuyết:
.............
II. Luyện tập:
Bài tập 41( SGK trang 132)
a, Diện tớch tam giỏc DBE là:
 S = DE. BC = . 6. 6,8 
 = 20,4( cm2)
b, Diện tớch tứ giỏc EHIK là:
Theo GT ta cú: 
cm
cm
Vậy: 
SCHE = CE . HC : 2 = 3,4 .6:2
 = 10,2cm2
SCIK = CI . KC : 2 = 1,7 . 3: 2
 = 7,65 cm2 
Vậy diện tớch tứ giỏc EHIK là:
S = 10,2 - 7,65 = 2,55 ( cm2)
Bài tập 35 (sgk trang 129)
ABCD là hỡnh thoi nờn AB = AD ABD cõn, lại cú gúc A = 600
 ABD là tam giỏc đều cú AH là đường cao nờn AH là trung tuyến
AH = HD = 6: 2 = 3 cm
Ta cú ABH vuụng tại H nờn 
BH = = cm
SABD =AD . BH : 2 = 6.: 2
 3. cm2
Vậy S ABCD =2.3. cm2 
 = 6. cm2
Bài 42 SGK trang 132
F
D
C
B
A
AC // BF
Ta cú AC // BF nờn 
SABC = SAFC
 Suy ra SABC + SADC = SAFC + SADC
Hay SABCD = SADF
A
K
H
B
C
D - Củng cố:
	- Xem lại lí thuyết và các bài đã chữa
- Cho tam giác ABC biết AB = 3AC. 
Tính tỉ số 2 đường cao xuất phát từ các đỉnh B và C
E - Hướng dẫn về nhà
- Học bài theo tài liệu SGK, 
- Làm hoàn chỉnh bài tập đó HD trờn lớp
- Làm bài tập bổ sung ở sỏch bài tập.
-------------------------------------------
Ngày soan:
Ngày giảng:
 Tiết 15: Diện tích hình thoi
I- Mục tiêu:
- Kiến thức: HS nắm vững công thức tính diện tích hình thoi, biết cách tính diện tích 1 tứ giác có 2 đường chéo vuông góc với nhau.
- Hiểu được để chứng minh định lý về diện tích hình thoi
- Kỹ năng: Vận dụng công thức và tính chất của diện tích để tính diện tích hình thoi.
- Biết cách vẽ hình chữ nhật hay hình bình hành có diện tích bằng diện tích hình bình hành cho trước.
- HS có kỹ năng vẽ hình 
- Thái độ: Kiên trì trong suy luận, cẩn thận, chính xác trong hình vẽ.
 - Tư duy nhanh, tìm tòi sáng tạo.
II- phương tiện thực hiện:
- GV: Bảng phụ, dụng cụ vẽ.
- HS: Thứơc com pa, đo độ, ê ke.
III. cách thức tiến hành: 
- Dạy học đặt và giải quyết vấn đề
III- Tiến trình bài dạy
A - Tổ chức:
Lớp 8A: 	8B: 
B - Kiểm tra:
 a) Phát biểu định lý và viết công thức tính diện tích của hình thang, hình bình hành?
 b) Khi nối chung điểm 2 đáy hình thang tại sao ta được 2 hình thang có diện tích bằng nhau?
C- Bài mới: 
Hoạt động của giáo viên
Hoạt động của học sinh
1- Cách tính diện tích 1 tứ giác có 2 đường chéo vuông góc
- Hãy tính diện tích tứ giác ABCD theo AC và BD biết AC BD
- GV: Em nào có thể nêu cách tính diện tích tứ giác ABCD?
- GV: Em nào phát biểu thành lời về cách tính diện tích tứ giác có 2 đường chéo vuông góc?
- GV: chốt lại
* Diện tích của tứ giác có 2 đường chéo vuông góc với nhau bằng nửa tích của 2 đường chéo đó.
2- Công thức tính diện tích hình thoi.
- Hãy viết công thức tính diện tích hình thoi
 theo 2 đường chéo.
- GV: Hình thoi có 2 đường chéo vuông góc với nhau nên ta áp dụng kết quả bài tập trên ta suy ra công thức tính diện tích hình thoi
Hãy tính diện tích hình thoi bằng cách khác 
1- Cách tính diện tích 1 tứ giác có 2 đường chéo vuông góc
SABC = AC.BH
SADC = AC.DH
Theo tính chất diện tích đa giác ta có
S ABCD = SABC + SADC = AC.BH + AC.DH
 = AC(BH + DH) = AC.BD
2- Công thức tính diện tích hình thoi.
* Định lý: 
Diện tích hình thoi bằng nửa tích hai đường chéo
S = d1.d2
3. Tống kết
D- Củng cố:
- Nhắc lại các công thức tính diện tích tứ giác
- Bài 44/ SBT	Cho hình thoi ABCD, biết AB = 5cm, AI = 3cm (I là giao điểm của 2 
 đường chéo). Tính diện tích hình thoi đó.
- Bài 45/ SBT	
E- Hướng dẫn về nhà
+ Làm các bài tập phần bài tập bổ sung.
+ Giờ sau luyện tập
----------------------------------------------------
Ngày soan:
Ngày giảng:
Tiết 16: Luyện tập
I- Mục tiêu:
- Kiến thức: HS nắm vững công thức tính diện tích hình thoi, biết cách tính diện tích 1 tứ giác có 2 đường chéo vuông góc với nhau. Hiểu được để chứng minh định lý về diện tích hình thoi
- Kỹ năng: Vận dụng công thức và tính chất của diện tích để tính diện tích hình thoi.
- Biết cách vẽ hình chữ nhật hay hình bình hành có diện tích bằng diện tích hình bình hành cho trước. HS có kỹ năng vẽ hình 
- Thái độ: Kiên trì trong suy luận, cẩn thận, chính xác trong hình vẽ.
 - Tư duy nhanh, tìm tòi sáng tạo.
II- phương tiện thực hiện:
- GV: Bảng phụ, dụng cụ vẽ.
- HS: Thứơc com pa, đo độ, ê ke.
III. cách thức tiến hành: 
- Luyện giải bài tập
IV- Tiến trình bài dạy
A- Tổ chức:
Lớp 8A: 	8B:
B- Kiểm tra:
- Phát biểu định lý và viết công thức tính diện tích của hình thoi?
C- Bài mới
- GV: ta đã có công thức tính diện tích hình thoi là 1 hình bình hành đặc biệt. Vậy áp dụng công thức vào để tính diện tích hình thoi .
Hoạt động của GV và HS
Nội dung ghi bảng
1) Chữa bài 32
- 2 HS lên bảng chữa bài 32
2. Chữa bài 33:
- GV: Cho HS làm bài 33/128
- GV hướng dẫn HS cách vẽ hình.
- GV hướng dẫn HS chứng minh ACFE & ABCD có cùng diện tích
3) Chữa bài 34
Vẽ hình chữ nhật ABCD với các trung điểm của các cạnh là M, N, P, Q Vẽ tứ giác MNPQ. Tứ giác này là hình thoi vì sao ? 
- So sánh diện tích hình thoi và diện tích hình chữ nhật?
- GV yêu cầu HS suy ra cách tính diện tích hình thoi?
Bài 32:
a) Vẽ được vô số tứ giác theo yêu cầu của đề bài:
 AC = 6 cm
 BD = 3,6 cm
 AC BD
 SABCD = AC . BD = 6.3,6 = 10,8 cm2
b) Hình vuông có 2 đường chéo vuông góc với nhau và mỗi đường chéo có độ dài là d, nên diện tích bằngd2
Bài 33:
Vẽ hình thoi ABCD theo 2 đường chéo BD & AC vuông góc tại trung điểm mỗi đường
- Vẽ hình chữ nhật ACFE có: AE = BH
-Chứng minh ACFE & ABCD có cùng diện tích
6 vuông trong hình vẽ bằng nhau
+áp dụng tính chất của diện tích đa giác ta có:
 SABCD = SACEF
+ Theo công thức tính diện tích hình chữ nhật ta có: SACEF = AC.BH
+ Theo công thức tính diện tích hình thoi:
 SABCD = AC.BH = BD. AC
Bài 34
a) tứ giác MNPQ là hình thoi vì có bốn cạnh bằng nhau
b) 
SMNPQ = SABCD = AB. BC = MP. NQ
 = AB.AD = S ABCD
 A N B
 M P
 I 
 D Q C
D- Củng cố:
- GV: Nhắc lại cách chứng minh
- Hướng dẫn cách giải bài tập bổ sung ở SBT trang 163
E- Hướng dẫn về nhà
- Xem lại bài đã chữa
- Tự ôn tập phần chương II.
- Ôn tập lại phần phương trình.
-----------------------------------------
Thay co nao muon lay de chinh sua hay goi toi theo so sau: 0943798725
Ngày soạn:
Ngày giảng:
Tiết 17 Luyện tập về phương trình được đưa về dạng ax + b = 0
I. Mục tiêu:
- Kiến thức: - HS hiểu cách biến đổi phương trình đưa về dạng ax + b = 0 
+ Hiểu được và sử dụng qui tắc chuyển vế và qui tắc nhân để giải các phương trình 
- Kỹ năng: áp dụng 2 qui tắc để giải phương trình bậc nhất 1 ẩn số 
- Thái độ: Tư duy lô gíc - Phương pháp trình bày
II. phương tiện thực hiện
- GV: Bài soạn.bảng phụ
- HS: bảng nhóm
III. cách thức tiến hành:
Dạy học nêu và giải quyết vấn đề.
Dạy học hợp tác trong nhóm nhỏ.
IV. Tiến trình bài dạy
A- Tổ chức:
 Lớp 8A: 	8B: 
B- Kiểm tra:
	Nêu các bước giải phương trình đưa được về dạng ax + b = 0 
- Bước 1: Quy đồng, khử mẫu (nếu có)
- Bước 2: Biến đổi PT (phá ngoặc, chuyển vế, rút gọn) đưa PT về dạng mx = n
- Bước 3: Kết luận nghiệm PT
C- Baì mới:
Hoạt động của GV và HS
Nội dung ghi bảng
Bài tập
I- Bài tập Giải PT sau
D- Củng cố
- Nêu các bước giải phương trình đưa được vế pt bậc nhất một ẩn
E- Hướng dẫn về nhà
- Làm các bài tập ở SBT