Giáo án phụ đạo môn Toán Lớp 8 - Buổi 8 - Nguyễn Hữu Vinh
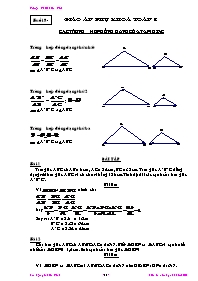
Trường hợp đồng dạng thứ nhất
ABC ABC
Trường hợp đồng dạng thứ 2
;
ABC ABC
Trường hợp đồng dạng thứ ba
ABC ABC
BÀI TẬP
Bài 1
Tam giác ABC có AB = 8cm, AC = 24 cm, BC = 32cm. Tam giác ABC đồng dạng với tam giác ABC và có chu vi bằng 128cm. Tính độ dài các cạnh của tam giác ABC.
Bạn đang xem tài liệu "Giáo án phụ đạo môn Toán Lớp 8 - Buổi 8 - Nguyễn Hữu Vinh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Buổi 8. Giáo án phụ khoá toán 8 các trường hợp đồng dạng của tam giác Trường hợp đồng dạng thứ nhất S DA’B’C’ DABC Trường hợp đồng dạng thứ 2 ; S DA’B’C’ DABC Trường hợp đồng dạng thứ ba S DA’B’C’ DABC Bài tập Bài 1 Tam giác ABC có AB = 8cm, AC = 24 cm, BC = 32cm. Tam giác A’B’C’ đồng dạng với tam giác ABC và có chu vi bằng 128cm. Tính độ dài các cạnh của tam giác A’B’C’. Bài làm S Vì nên ta có: hay Suy ra: A’B’ = 2.8 = 16 cm B’C’ = 2.32 = 64 cm A’C’ = 2.24 = 48 cm Bài 2 S Cho tam giác ABC có AB:BC:AC = 5: 6: 7. Biết DEF ABC và cạnh nhỏ nhất của DEF là 1,5 cm. tính cạnh của tam giác DEF? Bài làm S Vì DEF ABC mà AB:BC:AC = 5: 6: 7 nên DE : EF : DF = 5: 6: 7. Nghĩa là Cạnh nhỏ nhất của tam giác DEF là DE do đó DE = 1,5 cm. Từ đó ta có: = Bài 3 Cho hình thang ABCD có , AB = 2 cm, BD = 4cm, CD = 8cm. S a, Chứng minh ABD BDC. b, Tính BC Bài làm a, Ta có: ; Suy ra = . Mặt khác (Hai góc so le trong) S Do đó ABD BDC. (Trường hợp đồng dạng thứ 2) S b, ABD BDC nên Trong tam giác vuông BCD ta có: BC2 = CD2 - BD2 = 82 - 42 = 48 BC = Bài 4 Cho tam giác ABC, phân giác AD. Qua B kẻ tia Bx sao cho . Tia Bx cắt tia AD tại E. Chứng minh: S a, ABE ADC. b, BE2 = AD.AE Bài làm a, AD là phân giác của góc BAC, nên (theo giả thiết) Ta lại có: (Hai góc đối đỉnh). Từ đó đối với hai tam giác BDE và ADC ta có . ABE và ADC có: S Do đó ABE ADC. b, ABE và BDE có: S chung BAE DBE Bài 5 Cho tam giác ABC, có , AC = 4cm, BC = 6cm. Trên tia đối của tia AC lấy điểm E sao cho AE = AC. S a, Chứng minh ABC BAE b, Tính độ dài AB Bài làm a, Do AE = AB (gt) nên AED cân ở A S Mặt khác ABC BAE S b, ABC BEC (Theo câu a) ta có: Ngày /4/09 Xác nhận của chuyên môn
Tài liệu đính kèm:
 giao_an_phu_dao_mon_toan_lop_8_buoi_8_nguyen_huu_vinh.doc
giao_an_phu_dao_mon_toan_lop_8_buoi_8_nguyen_huu_vinh.doc





