Giáo án phụ đạo môn Toán Lớp 8 - Buổi 4 - Nguyễn Hữu Vinh
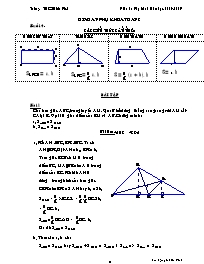
Bài 1
Cho tam giác ABC, trung tuyến AM. Qua B kẻ đường thẳng song song với AM cắt CA tại E. Gọi I là giao điểm của EM và AB. Chứng minh:
a, SABC = S MEC
b, S IEA = S IMB
Bài làmABC = CDA
a, Kẻ AH BC, EK BC. Ta có AH//EK, Đặt AH = h1, EK = h2
Tam giác ECB có M là trung điểm BC, MA//BE nên A là trung điểm của EC. Khi đó AH là đường trung bình của tam giác CEK nên EK = 2 AH hay h2 = 2h1
S MEC = MC.EK = .BC.2h2
= BC. h1
SABC =BC.AH = BC. h1
Do đó SABC = S MEC
Bạn đang xem tài liệu "Giáo án phụ đạo môn Toán Lớp 8 - Buổi 4 - Nguyễn Hữu Vinh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Giáo án phụ khoá toán 8 Buổi 4. Các kiến thức cần nhớ: Hình chữ nhật Tam giác Hình thang Hình bình hành SABCD = a.b SABC = a.h S = (a + b).h S = a.h Bài tập Bài 1 Cho tam giác ABC, trung tuyến AM. Qua B kẻ đường thẳng song song với AM cắt CA tại E. Gọi I là giao điểm của EM và AB. Chứng minh: a, SABC = S MEC b, S IEA = S IMB Bài làmDABC = DCDA a, Kẻ AH BC, EK BC. Ta có AH//EK, Đặt AH = h1, EK = h2 Tam giác ECB có M là trung điểm BC, MA//BE nên A là trung điểm của EC. Khi đó AH là đường trung bình của tam giác CEK nên EK = 2 AH hay h2 = 2h1 S MEC = MC.EK = .BC.2h2 = BC. h1 SABC =BC.AH = BC. h1 Do đó SABC = S MEC b, Theo câu a, ta có: SABC = S MEC hay SAIMC + S IMB = SAIMC + SIAE => S IEA = S IMB Bài 2 Cho tam giác ABC có đáy BC = 20cm và diện tích là 120cm2. a, Tính chiều cao AH của tam giác. b, Gọi M,N lần lượt là trung điểm của AB, AC. Tứ giác BMNC là hình gì? Tính diện tích của tứ giác đó. Bài làm a, Ta có: SABC =BC.AH => AH = == 12(cm) b, MN là đường trung bình của tam giác ABC nên MN//BC do đó tứ giác BMNC là hình thang. Gọi giao điểm của AH với MN là I, tam giác ABH có M là trung điểm của AB, MI//BH nên ta có IA = IH = 6cm MN là trung bình của tam giác ABC, ta có MN = BC = 10cm SBMNC =(BC + MN).IH = (20+10).6 = 90(cm2). Hoặc : SBMNC = SABC - SAMN = 120 - .10.6 = 90(cm2) Bài 3 Cho hình bình hành ABCD cạnh AB = 8cm, Khoảng cách từ giao điểm O của hai đường chéo đến AB, BC lần lượt bằng 3cm, 4cm. a, Tính diện tích hình bình hành. b, Tính độ dài cạnh BC. Bài làm a, Gọi OH là khoảng cách từ O đến AB, ta có OH AB. Tia HO cắt CD ở I thì HI CD. DOHA = DOCI (c.g.c) => OI = OH Do đó HI = 2OH = 6cm. SABCD = AB.HI = 8.6 = 48(cm2). b, Gọi OK là khoảng cách từ O đến BC, ta có OK BC, Tia OK cắt AD tại E thì KE AD và KE = 2OK = 8cm. SABCD = BC.KE => BC = = = 6 cm Bài 4 Cho tam giác ABC trung tuyến AM. Gọi I là trung điểm của AM. Tia CI cắt AB tại E. Gọi F là trung điẻm của EB. Biết diện tích tam giác ABC bằng 36m2. Tính diện tích tam giác BFC? Bài làm: a, MF là đường trung bình của tam giác BEC, => MF//CE. IE là đường trung bình của tam giác AMF ta có: AE = EF, mà EF = FB, do đó: FB = FA = EA = AB Tam giác BFC và tam giác ABC có chung chiều cao kẻ từ C xuống AB và có cạnh đáy BF = AB, do đó S BFC = S ABC = 12 m2 Bài 5 Cho hình chữ nhật ABCD, từ A và C kẻ AE, CF cùng vuông góc với BD a, Chứng minh rằng hai đa giác ABCFE và ADCFE có cùng diện tích. b,Tính diện tích của mỗi đa giác nói trên nếu các cạnh của hình chữ nhật là 16cm và 12cm. Bài làm: a,AED = CFB (Cạnh huyền – góc nhọn) => S AED= S CFB (1) AEB = CFD (Cạnh huyền – góc nhọn) => S AEB= S CFD (2) (1) và (2) => S AED + S CFD = S CFB + S AEB Hay S ADCFE = S ABCFE b, Vì S ADCFE + S ABCFE = S ABCD nên S ADCFE = S ABCFE = S ABCD = .16.12 => S ADCFE = S ABCFE = 96 (cm)2.
Tài liệu đính kèm:
 giao_an_phu_dao_mon_toan_lop_8_buoi_4_nguyen_huu_vinh.doc
giao_an_phu_dao_mon_toan_lop_8_buoi_4_nguyen_huu_vinh.doc





