Giáo án ôn luyện môn Toán Lớp 9
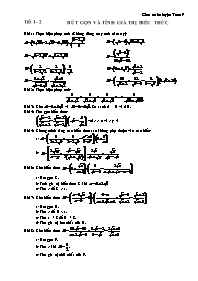
Bài 1: Thực hiện phép tính (Không dùng máy tính cầm tay):
Bài 2:
a/ Sắp xếp theo thứ tự từ nhỏ đến lớn: , ,
b/ Sắp xếp theo thứ tự giảm dần: , , ,
Bài 3: Không dùng máy tính cầm tay, hãy so sánh:
a/ và
c/ và
b/ và
d/ và
Bài 4: Cho hàm số . Không tính, hãy so sánh:
a/ và
b/ và
Bài 5: Chứng minh đẳng thức:
Bài 6: Rút gọn biểu thức với x > 0, y > 0, x ≠ y.
Bài 7: Cho biểu thức
a/ Rút gọn B.
b/ Tìm GTNN của B.
Bài 8: Cho biểu thức
a/ Rút gọn P.
b/ Tìm x để P <>
c/ Tìm x Z để P Z.
Bài 9: Cho biểu thức
Tìm GTNN và GTLN của Q.
Bạn đang xem tài liệu "Giáo án ôn luyện môn Toán Lớp 9", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Tiết 1 - 2 RÚT GỌN VÀ TÍNH GIÁ TRỊ BIỂU THỨC Bài 1: Thực hiện phép tính (Không dùng máy tính cầm tay): Bài 2: Thực hiện phép tính: Bài 3: Cho và . So sánh A + B và AB. Bài 4: Thu gọn biểu thức: với x > 0 và x ≠ 4 Bài 5: Chứng minh rằng các biểu thức sau không phụ thuộc vào các biến: a/ b/ Bài 6: Cho biểu thức a/ Rút gọn K. b/ Tính giá trị biểu thức K khi c/ Tìm x để K > 1. Bài 7: Cho biểu thức a/ Rút gọn H. b/ Tìm x để H < 1. c/ Tìm x Î Z để H Î Z. d/ Tìm giá trị lớn nhất của H. Bài 8: Cho biểu thức a/ Rút gọn P. b/ Tìm x khi . c/ Tìm giá trị nhỏ nhất của P. Tiết 3 - 4 RÚT GỌN VÀ TÍNH GIÁ TRỊ BIỂU THỨC (tt) Bài 1: Thực hiện phép tính (Không dùng máy tính cầm tay): Bài 2: a/ Sắp xếp theo thứ tự từ nhỏ đến lớn: , , b/ Sắp xếp theo thứ tự giảm dần: , , , Bài 3: Không dùng máy tính cầm tay, hãy so sánh: a/ và c/ và b/ và d/ và Bài 4: Cho hàm số . Không tính, hãy so sánh: a/ và b/ và Bài 5: Chứng minh đẳng thức: Bài 6: Rút gọn biểu thức với x > 0, y > 0, x ≠ y. Bài 7: Cho biểu thức a/ Rút gọn B. b/ Tìm GTNN của B. Bài 8: Cho biểu thức a/ Rút gọn P. b/ Tìm x để P < 1. c/ Tìm x Î Z để P Î Z. Bài 9: Cho biểu thức Tìm GTNN và GTLN của Q. Bài tập về nhà: 1.1; 1.2; 1.3; 1.4; 1.5; 1.9; 1.11; 1.12; 1.13 Tiết 5 - 6 ĐỒ THỊ HÀM SỐ y = ax + b VÀ y = ax2 Bài 1: Vẽ Parabol (P): và đường thẳng (d): trên cùng một hệ trục tọa độ. Tìm tọa độ các giao điểm của (P) và (d) bằng phương pháp đại số. Bài 2: Cho Parabol (P): và đường thẳng (d): . a/ Vẽ (P) và (d) trên cùng một hệ trục tọa độ. b/ Tìm tọa độ các giao điểm A và B của hai đồ thị bằng phương pháp đại số. c/ Viết phương trình đường trung trực của đoạn AB. Bài 3: Trong mặt phẳng tọa độ Oxy cho parabol (P): . a/ Vẽ (P). b/ Gọi M, N là hai điểm thuộc (P) có hoành độ lần lượt là 1 và – 2. Viết phương trình đường thẳng MN. c/ Viết phương trình đường thẳng (d) song song với MN và tiếp xúc với (P). Bài 4: Cho (P): . a/ Tìm a biết (P) đi qua . b/ Trên (P) lấy điểm B có hoành độ bằng – 2. Viết phương trình đường thẳng AB. Bài 5: Cho (P): và (d): . a/ Tìm a biết (P) đi qua . b/ Chứng minh rằng (d) tiếp xúc với (P). Tìm tọa độ tiếp điểm. c/ Viết phương trình đường thẳng (d’) vuông góc với (d) tại A. Bài 6: Cho (P): . Viết phương trình đường thẳng (d) đi qua và tiếp xúc với (P). Bài 7: Cho (P): và (d): . a/ Chứng minh rằng (d) luôn cắt (P) tại 2 điểm A, B phân biệt. b/ Tìm m sao cho . Bài 8: Cho Parabol (P): và đường thẳng (d):. a/ Tìm m để (d) cắt (P) tại điểm có hoành độ bằng – 2. b/ Tìm m để (d) tiếp xúc với (P). Tìm tọa độ tiếp điểm. c/ Tìm m để (d) cắt (P) tại hai điểm có hoành độ dương. d/ Tìm m sao cho (d) cắt (P) tại hai điểm A, B thỏa mãn: . Bài 9: Cho Parabol (P): y = x2 và đường thẳng (d): y = mx – 2 (m là tham số, m ≠ 0) a/ Vẽ đồ thị (P) trên mặt phẳng Oxy. b/ Khi m = 3, tìm tọa độ giao điểm của (P) và (d). c/ Gọi , là hai giao điểm phân biệt của (P) và (d). Tìm các giá trị của m sao cho . Bài 10: Trong mặt phẳng toạ độ Oxy cho hàm số có đồ thị (P). a/ Tìm a, biết rằng (P) cắt đường thẳng (d) có phương trình tại điểm A có hoành độ bằng 3. Vẽ đồ thị (P) ứng với a vừa tìm được. b/ Tìm toạ độ giao điểm thứ hai B (khác A) của (P) và (d). Tiết 7 - 8 ĐỒ THỊ HÀM SỐ y = ax + b VÀ y = ax2 (tt) Bài 1: Cho đường thẳng (d): với k là tham số. a/ Tìm k để (d) đi qua điểm b/ Tìm k để (d) song song với đường thẳng . c/ Tìm k để (d) vuông góc với đường thẳng . d/ Chứng minh rằng không có giá trị k nào để (d) đi qua điểm . e/ Chứng minh rằng khi k thay đổi, đường thẳng (d) luôn đi qua một điểm cố định. Bài 2: Cho hàm số có đồ thị (P) và hàm số có đồ thị (d). a/ Chứng minh (d) luôn đi qua một điểm M cố định. b/ Tìm a để (P) đi qua điểm M cố định đó. c/ Viết phương trình đường thẳng (d’) qua M và tiếp xúc với (P). Bài 3: Cho parabol (P): và đường thẳng (d): . a/ Vẽ đồ thị (P). b/ Tìm m sao cho (d) tiếp xúc với (P). c/ Chứng tỏ rằng (d) luôn đi qua một điểm cố định A thuộc (P). Bài 4: Cho hàm số . a/ Vẽ đồ thị (P) của hàm số. b/ Gọi (d) là đường thẳng có hệ số góc k và đi qua điểm . Xác định k để (d) cắt (P) tại hai điểm A, B sao cho M là trung điểm của đoạn AB. Bài 5: Cho hàm số có đồ thị (d). a/ Vẽ (d) trên mặt phẳng tọa độ Oxy. b/ Gọi giao điểm của (d) với các trục Ox, Oy lần lượt là A và B. Tính chu vi DOAB và khoảng cách từ điểm O đến đường thẳng AB. Bài 6: Cho hàm số: có đồ thị (P) và đường thẳng (d): a/ Vẽ (d) và (P) trên cùng hệ trục tọa độ Oxy. b/ Tìm tọa độ giao điểm A, B của (d) và (P). Tính chu vi DAOB. c/ Tìm tọa độ điểm C thuộc Ox để chu vi DABC đạt giá trị nhỏ nhất. Bài 7: Cho hàm số: có đồ thị (P). a/ Tìm tọa độ các điểm A, B thuộc (P) có hoành độ lần lượt là – 1 và 2. b/ Viết phương trình đường thẳng AB. c/ Viết phương trình đường thẳng tiếp xúc với (P) và vuông góc với AB. Tìm tọa độ tiếp điểm. d) Tìm điểm C thuộc cung AB của (P) sao cho DABC cân tại C. Bài tập về nhà: 4.1; 4.3; 4.4; 4.5; 4.7; 4.8; 4.9; 4.10; 4.11; 4.12; 4.16 Tiết 9 – 10 PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH Bài 1: Giải các hệ phương trình: a/ b/ c/ d/ e/ f/ g/ h/ i/ Bài 2: Giải các phương trình sau: a/ b/ c/ d/ e/ f/ Bài 3: Giải các phương trình sau: a/ b/ c/ d/ e/ f/ g/ h/ i/ Bài 4: Cho hệ phương trình (m là tham số) a/ Giải hệ phương trình khi m = 2. b/ Chứng minh hệ phương trình luôn có nghiệm duy nhất với mọi m. Bài 5: Cho hệ phương trình (m là tham số) a/ Giải hệ phương trình với m = 2; b/ Chứng minh rằng với mọi giá trị của m thì hệ phương trình luôn có nghiệm duy nhất (x ; y) thoả mãn 2x + y ≤ 3. Bài 6: Cho hệ phương trình (m là tham số) (I). a) Giải hệ (I) với m = 1. b) Tìm tất cả các giá trị của m để hệ (I) có nghiệm duy nhất. Bài 7: Cho hệ phương trình a/ Giải hệ phương trình khi m = 3. b/ Tìm m nguyên để hệ có nghiệm duy nhất nguyên. Tiết 11 – 12 PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH (tt) Bài 1: Cho phương trình a/ Tìm m để phương trình có hai nghiệm phân biệt x1, x2. b/ Đặt . + Tìm m sao cho A = 20. + Tìm giá trị nhỏ nhất của A. Bài 2: Cho phương trình: (*) a/ Giải phương trình (*) khi m = 3. b/ Chứng minh phương trình (*) luôn có hai nghiệm phân biệt x1, x2 Bài 3: Cho phương trình a/ Giải phương trình với m = 1. b/ Chứng minh rằng giá trị của biểu thức không phụ thuộc vào m. Bài 4: Cho phương trình . a/ Giải phương trình với m = 1. b/ Tìm các giá trị của m để phương trình có hai nghiệm x1, x2 thỏa mãn . Bài 5: Cho phương trình (1) a. Tìm m để pt (1) có nghiệm. b. Giả sử x1, x2 là hai nghiệm của phương trình (1). Tìm m để . Bài 6: Cho phương trình: (với m là tham số, m ≠ 1) a/ Chứng tỏ phương trình luôn có hai nghiệm phân biệt. b/ Tìm m sao cho hai nghiệm x1, x2 thỏa mãn . c/ Tìm hệ thức giữa x1, x2 không phụ thuộc vào m. Bài 7: Cho phương trình bậc hai: a/ Chứng minh rằng phương trình luôn có nghiệm với mọi m. b/ Gọi x1, x2 là các nghiệm của phương trình. Chứng minh: . Bài 8: Cho phương trình (x là ẩn số) a/ Chứng minh phương trình luôn luôn có 2 nghiệm phân biệt với mọi giá trị m. b/ Gọi x1, x2 là các nghiệm của phương trình. Tìm m để biểu thức sau đạt giá trị lớn nhất: A = . Bài 9: Cho phương trình (với m là tham số). a/ Giải phương trình với m = 2. b/ Chứng minh rằng phương trình luôn có nghiệm. c/ Gọi hai nghiệm của phương trình là x1, x2, hãy tìm giá trị bé nhất của . Bài 10: Giải hệ phương trình: Bài 11: Cho x, y là hai số nguyên dương sao cho: . Tính x2 + y2. Tiết 13 – 14 PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH (tt) Bài 1: Cho phương trình bậc hai . Gọi hai nghiệm của phương trình là x1, x2. Không giải phương trình, hãy lập phương trình bậc hai có hai nghiệm là và . Bài 2: Lập phương trình bậc hai có hai nghiệm là và . Bài 3: Lập phương trình bậc hai có hai nghiệm là x1 và x2 thỏa : Bài 4: Cho hệ phương trình: . Gọi nghiệm của hệ là (x ; y). Tìm a để bé nhất. Bài 5: Cho phương trình a/ Giải phương trình với m = 1. b/ Tìm m để phương trình có hai nghiệm trái dấu. c/ Tìm m để phương trình có một nghiệm bằng 3. Tìm nghiệm kia. Bài 6: Cho phương trình a/ Chứng minh phương trình luôn có nghiệm với mọi m. b/ Tìm hệ thức liên hệ giữa hai nghiệm mà không phụ thuộc vào m. c/ Tìm m để phương trình có hai nghiệm là 2 số nghịch đảo của nhau. d/ Tìm m để phương trình có hai nghiệm là hai số đối nhau. e/ Lập phương trình bậc hai có hai nghiệm u, v sao cho u = x1 + 2, v = x2 + 2. Bài 7: Cho phương trình a/ Tìm m để phương trình có nghiệm. b/ Tìm m để phương trình có hai nghiệm x1, x2 thỏa x1 = 3x2. Bài 8: a/ Cho phương trình . Tìm m để phương trình có hai nghiệm phân biệt sao cho nghiệm này gấp đôi nghiệm kia. b/ Cho phương trình . Tìm m để phương trình có hai nghiệm phân biệt x1, x2 sao cho 2x1 + 3x2 = 13. Bài 9: Cho phương trình với m là tham số: (1). a) Tìm m để phương trình (1) có nghiệm. b) Tìm m để phương trình (1) có hai nghiệm sao cho nghiệm này gấp ba lần nghiệm kia. Bài 10: Cho phương trình (1). a/ Giải phương trình với m = 1. b/ Tìm m để phương trình có hai nghiệm trái dấu. c/ Chứng minh rằng phương trình luôn có hai nghiệm phân biệt mà mỗi nghiệm của nó là nghịch đảo mỗi nghiệm của phương trình (1). Bài 11: Giải các hệ phương trình: a/ b/ c/ Bài tập về nhà: 2.1; 2.3 ® 2.17 Tiết 15 – 16 PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH (tt) TÓM TẮT PHƯƠNG PHÁP GIẢI: 1/ Dạng 1: Điều kiện: A(x) ³ 0 hoặc B(x) ³ 0. Bình phương hai vế được phương trình A(x) = B(x). 2/ Dạng 2: Điều kiện: B(x) ³ 0. Bình phương hai vế được phương trình . Bài 1: Giải các phương trình sau: a/ b/ c/ d/ e/ f/ g/ h/ i/ Bài 2: Giải các phương trình sau: a/ b/ c/ d/ e/ Bài 3: Giải các phương trình sau: a/ b/ c/ d/ Tiết 19 – 20 CÁC BÀI TOÁN TÌM GTLN - GTNN Bài 1: Tìm GTNN của các biểu thức sau: a/ b/ c/ d/ e/ f/ g/ h/ Bài 2: Tìm GTLN của các biểu thức sau: a/ b/ c/ d/ e/ f/ Bài 3: Cho phương trình: a/ Chứng tỏ phương trình luôn có hai nghiệm phân biệt x1, x2 với mọi m. b/ Cho . Tìm GTNN của B và giá trị tương ứng của m. Bài 4: Cho phương trình: a/ Chứng tỏ phương trình luôn có hai nghiệm trái dấu x1, x2 với mọi m. b/ Tìm m để đạt GTNN. Bài 5: Tìm GTNN của biểu thức: Bài 6: Cho . Tìm GTLN và GTNN của . Tiết 21 – 24 CÁC BÀI TOÁN GIẢI BẰNG CÁCH LẬP PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH DẠNG 1: TOÁN CHUYỂN ĐỘNG Bài 1: Một ôtô đi từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc 35 km/h thì đến chậm mất 2 giờ. Nếu xe chạy với vận tốc 50 km/h thì đến sớm hơn 1 giờ. Tính quãng đường AB và thời gian dự định đi lúc đầu. Bài 2: Một người đi xe máy từ A đến B cách nhau 120 km với vận tốc dự định trước. Sau khi được 1/3 quãng đường AB, người đó tăng vận tốc thêm 10 km/h nên đã đến B sớm hơn dự định 24 phút. Tìm vận tốc dự định và thời gian xe lăn bánh trên đường. Bài 3: Khoảng cách giữa hai thành phố A và B là 180km. Một ô tô đi từ A đến B, nghỉ 90 phút ở B rồi lại đi về A. Biết rằng vận tốc lúc về kém vận tốc lúc đi là 5km/h và thời gian từ lúc đi đến lúc về là 10 giờ. Tìm vận tốc lúc đi của ô tô. Bài 4: Quãng đường AB dài 180km. Cùng lúc có hai ô tô khởi hành từ A để đến B. Do vận tốc của ô tô thứ nhất hơn vận tốc của ô tô thứ hai 15km/h nên ô tô thứ nhất đến B sớm hơn 2 giờ. Tìm vận tốc của mỗi ô tô. Bài 5: Một canô xuôi dòng từ A đến B, sau đó lại ngược dòng từ B trở về A với cùng vận tốc 30 km/h. Thời gian đi xuôi dòng ít hơn thời gian đi ngược dòng là 1 giờ 12 phút. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc dòng nước là 5 km/h. Bài 6: Một canô xuôi dòng từ A đến B dài 80km, sau đó lại ngược dòng đến C cách B 72km. Thời gian xuôi dòng ít hơn thời gian ngược dòng là 15 phút. Tính vận tốc của canô, biết rằng vận tốc dòng nước là 4km/h. Bài 7: Hai người cùng khởi hành đi ngược chiều nhau, người thứ nhất đi từ A đến B, người thứ hai đi từ B đến A. Họ gặp nhau sau 3 giờ. Hỏi mỗi người đi quãng đường AB trong bao lâu, nến người thứ nhất đến B muộn hơn người thứ hai đến A là 2,5 giờ. Bài 8: Một ca nô xuôi dòng từ bến sông A đến bến sông B cách nhau 24km, cùng lúc đó một bè nứa cũng trôi từ A với vận tốc 4km/h. Khi đến B ca nô quay lại ngay và gặp bè nứa tại địa điểm C cách A là 8km. Tính vận tốc thực của ca nô. DẠNG 2: TOÁN NĂNG SUẤT Bài 9: Hai người thợ cùng làm chung một công việc trong 7 giờ 12 phút thì xong. Nếu người thứ nhất làm trong 5 giờ và người thứ hai làm trong 6 giờ thì cả hai người chỉ làm được công việc. Hỏi một người làm công việc đó trong mấy giờ thì xong? Bài 10: Hai người cùng làm chung một công việc thì hoàn thành trong 4 giờ. Nếu làm riêng để hoàn thành công việc thì thời gian của người thứ nhất ít hơn thời gian của người thứ hai là 6 giờ. Hỏi nếu làm riêng thì mỗi người sẽ hoàn thành công việc trong bao lâu? Bài 11: Một đội xe cần phải chuyên chở 150 tấn hàng. Hôm làm việc có 5 xe được điều đi làm nhiệm vụ khác nên mỗi xe còn lại phải chở thêm 5 tấn. Hỏi đội xe ban đầu có bao nhiêu chiếc? Bài 12: Hai vòi nước cùng chảy vào 1 cái bể không có nước trong 6 giờ thì đầy bể. Nếu để riêng vòi thứ nhất chảy trong 2 giờ, sau đó đóng lại và mở vòi thứ hai chảy tiếp trong 3 giờ nữa thì được 2/5 bể. Hỏi nếu chảy riêng thì mỗi vòi chảy đầy bể trong bao lâu? Bài 13: Hai máy ủi làm việc trong vòng 12 giờ thì san lấp được 1/10 khu đất. Nếu máy ủi thứ nhất làm một mình trong 42 giờ rồi nghỉ và sau đó máy ủi thứ hai làm một mình trong 22 giờ thì cả hai máy ủi san lấp được 25% khu đất đó. Hỏi nếu làm một mình thì mỗi máy ủi san lấp xong khu đất đã cho trong bao lâu. Bài 14: Một đội công nhân phải làm 216 sản phẩm trong một thời gian nhất định. Ba ngày đầu, mỗi ngày đội làm đúng theo định mức. Sau đó mỗi ngày họ đều làm vượt mức 8 sản phẩm nên đã làm xong 232 sản phẩm trước thời hạn 1 ngày. Hỏi theo kế hoạch mỗi ngày đội phải làm bao nhiêu sản phẩm? DẠNG 3: TOÁN CÓ NỘI DUNG HÌNH HỌC Bài 15: Một khu vườn hình chữ nhật có chu vi là 280m. Người ta làm lối đi xung quanh vườn rộng 2m (thuộc đất trong vườn). Tính kích thước của khu vườn, biết rằng diện tích đất còn lại để trồng trọt là 4256m2. Bài 16: Cho một hình chữ nhật. Nếu tăng chiều dài 10m và tăng chiều rộng 5m thì diện tích tăng 500m2. Nếu giảm chiều dài 15m và giảm chiều rộng 9m thì diện tích giảm 600m2. Tính chiều dài, chiều rộng ban đầu. Bài 17: Một hình chữ nhật có diện tích 300m2. Nếu giảm chiều rộng 3m và tăng chiều dài 5m thì diện tích không đổi. Tìm kích thước của hình chữ nhật ban đầu. Bài 18: Một tam giác vuông có cạnh huyền là 5cm và diện tích là 6cm2. Tính độ dài hai cạnh góc vuông. Bài 19: Một hình chữ nhật có chiều dài hơn chiều rộng 7m và có độ dài đường chéo là 17m. Tính chu vi và diện tích của hình chữ nhật. Bài 20: Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 22m. Nếu giảm chiều dài 2m và tăng chiều rộng 3m thì diện tích sẽ tăng thêm 70m2. Tính chiều dài và chiều rộng của mảnh đất đó. DẠNG 4: TOÁN VỀ TÌM SỐ Bài 21: Tìm hai số biết hiệu của chúng bằng 10 và tổng của 6 lần số lớn với 2 lần số bé là 116. Bài 22: Tìm một số tự nhiên có hai chữ số, biết rằng tổng các chữ số bằng 11 và nếu đổi chỗ chữ số hàng chục và chữ số hàng đơn vị cho nhau thì số đó tăng thêm 27 đơn vị. Bài 23: Tìm một số có hai chữ số, biết rằng số đó gấp 7 lần chữ số hàng đơn vị của nó và nếu lấy số cần tìm chia cho tổng các chữ số của nó thì được thương là 4 và số dư là 3. Bài 24: Nếu tử số của một phân số được tăng gấp đôi và mẫu số thêm 8 thì giá trị của phân số bằng . Nếu tử số thêm 7 và mẫu số tăng gấp 3 thì giá trị phân số bằng . Tìm phân số đó. Bài 25: Nếu thêm 4 vào cả tử và mẫu của một phân số thì giá trị của phân số giảm 1. Nếu bớt 1 ở cả tử và mẫu thì giá trị của phân số tăng . Tìm phân số ban đầu. Bài 26: Tìm số tự nhiên có 2 chữ số, biết rằng tổng của hai chữ số bằng 1/8 số đó, còn nếu thêm 13 vào tích của hai chữ số thì được số viết theo thứ tự ngược lại với số đã cho. DẠNG 5: NỘI DUNG KHÁC Bài 27: Hai lớp 9A và 9B có tổng số học sinh là 84. Trong đợt mua bút ủng hộ nạn nhân chất độc màu da cam, mỗi học sinh lớp 9A mua 3 chiếc bút, mỗi học sinh lớp 9B mua 2 chiếc bút. Tìm số học sinh mỗi lớp, biết tổng số bút hai lớp mua là 209 chiếc. Bài 28: Hai tổ sản suất cùng may một loại áo. Nếu tổ thứ nhất may trong 3 ngày, tổ thứ hai may trong 5 ngày thì cả hai tổ may được 1310 chiếc áo. Biết rằng trong mỗi ngày tổ thứ nhất may được nhiều hơn tổ thứ hai 10 chiếc áo. Hỏi mỗi tổ may trong một ngày được bao nhiêu chiếc áo? HƯỚNG DẪN GIẢI: Bài 8: Gọi x (km/h) là vận tốc thực của canô (x > 0). Vận tốc xuôi dòng: x + 4 (km/h). Vận tốc ngược dòng: x – 4 (km/h). Thời gian xuôi dòng từ A đến B: (h). Thời gian ngược dòng từ B về C: (h). Ta có phương trình: . Giải phương trình tìm được x = 20. Bài 14: Gọi x là số sản phẩm phải làm mỗi ngày theo kế hoạch. (x > 0) Thời gian dự định để làm 216 sản phẩm: (ngày) Số sản phẩm làm được 3 ngày đầu: 3x (sản phẩm). Số sản phẩm còn lại: 232 – 3x (sản phẩm). Số sản phẩm mỗi ngày làm được sau khi tăng năng suất: x + 8 (sản phẩm). Thời gian để hoàn thành 232 – 3x sản phẩm: Theo đề ta có phương trình: Giải được , (loại). Vậy theo kế hoạch mỗi ngày phải làm 24 sản phẩm.
Tài liệu đính kèm:
 giao_an_on_luyen_mon_toan_lop_9.doc
giao_an_on_luyen_mon_toan_lop_9.doc





