Giáo án môn Hình học Khối 8 - Tiết 11 đến 14 (Bản 4 cột)

Ngày soạn 2/10/04 TUẦN 6
Tiết 11	
LUYỆN TẬP
I. MỤC TIÊU:
- Củng cố kiến thức về 2 hình đối xứng nhau qua một đường thẳng (trục), vẽ hình có trục đối xứng.
- Rèn kỹ năng về hình đối xứng của một hình (dạng hình đơn giản) qua một trục đối xứng.
- Rèn kỹ năng nhận xét 2 hình đối xứng qua một trục, hình có trục đối xứng trang thế và cuộc sống.
II. CHUẨN BỊ:
Thầy: Thước thẳng, compa, bảng phụ, phấn màu
Hình vẽ 59 trang 87
Trò: Compa, thước thẳng, bảng nhóm.
III. TIẾN TRÌNH TIẾT DẠY:
1. Ổn định (1’)
2. Kiểm tra (10’) gọi 2 HS lên bảng
HS1: a) Nêu định nghĩa hai điểm đối xứng qua một đường thẳng?
b) Vẽ hình đối xứng của DABC qua đường thẳng d.
(Đáp: a) HS phát biểu định nghĩa theo SGK.
b) Vẽ
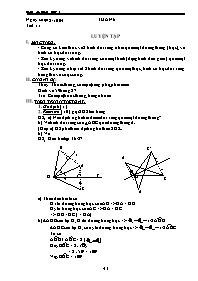
HS2: Giải bài tập 36/87
C’
A
C
A
A
B
x
y
C
1
2
3
4
 B’
 O B
a) Theo đầu bài ta có:
Ox là đường trung trực của AB => OA = OB
Oy là trung trực của AC => OA = OC
=> OB = OC ( = OA)
b) DAOB cân tại O, Ox là đường trung trực => 1/2 AOB
DAOC cân tại O, có oy là đường trung trực => 1/2AOC
Ta có:
AOB + AOC = 2 ()
Hay BOC = 2. xOy
	 = 2 . 500 = 1000
Vậy BOC = 1000
GV cho HS nhận xét. GV nhận xét chung và ghi điểm .
3. Bài mới:
TL
Hoạt động của thầy
Hoạt động của trò
Ghi bảng
5p
- Cho HS làm bài 37 trang 87 SGK
s Cho HS quan sát các hình vẽ (hình 59) trên bảng phụ.
s Yêu cầu HS tìm các hình có trục đối xứng gọi HS lên bảng vẽ trục đối xứng của mỗi hình.
- HS quan sát hình vẽ.
- 2 HS lên bảng vẽ trục đối xứng của các hình a, b, c, d, e, g, i
1. Bài 37/87 (SGK)
12p
- Cho HS làm bài 39/88.
s Gọi HS đọc đề, ngắt từng ý, yêu cầu HS vẽ hình theo lời GV đọc 
s 1 HS đọc đề
s 1 HS vẽ hình trên bảng, cả lớp vẽ hình vào vở.
A
BN
E
C
D
2. Bài 39/88 (SGK)
s GV ghi kết luận:
AD + DB < AE + EB
s Hãy phát hiện trên hình những cặp đoạn thẳng bằng nhau. giải thích?
s Vậy AD + DB = ?
AE + EB = ?
s Tại sao AD + DB lại nhỏ hơn AE + EB?
(GV vừa hướng dẫn HS tìm lời giải vừa ghi bảng)
s GV: như vậy nếu A và B là 2 điểm thuộc cùng 1 nửa mặt phẳng có bờ là đường thẳng d thì điểm D (giao điểm của CB với d) là điểm có tổng khoảng cách từ đó tới A và B là nhỏ nhất.
s Áp dụng câu a . hãy trả lời câu b 
- HS trả lời.
Ta có: AD = CD
Và AE = CE
- HS:
AD + DB = CD + DB = CB
AE + EB = CE + EB
- HS: có:
CB < CE + EB
=> AD + DB < AE + EB
a) Vì A và C đối xứng với nhau qua d nên d là đường trung trực của đoạn AC. Do đó:
AD = CD, AE = CE
Suy ra:
AD + DB = CD + DB = CB (1)
AE + EB = CE + EB (2)
Xét DCEB có:
CB < CE + EB (bdt trong tam giác) (3)
Từ (1), (2) và (3) suy ra:
AE + EB < AE + EB
b) Con đường ngắn nhất mà bạn Tú nên đi là.. đường ADB
5p
Cho HS giải bài 40/88 SGK
s GV đưa đề bài và hĩnh vẽ lên bảng phụ
s Yêu cầu HS quan sát, mô tả từng biển báo giao thông và quy định của luật giao thông.
- HS mô tả từng biển báo để ghi nhớ và thực hiện theo quy định.
s Biểu nào có trục đối xứng?
- HS: Biển a, b, d mỗi biển có một trục đối xứng.
Biển C không có trục đối xứng.
10p
GV đưa đề bài trên phiếu học tập, phát cho HS:
Vẽ hình đối xứng qua đường thẳng d của hình vẽ
d
Cho HS thi vẽ nhanh, vẽ đúng, vẽ đẹp. GV thu 10 bài tập nộp đầu tiên nhận xét, đánh giá và cho điểm.
s HS làm bài trên phiếu học tập
4. Dặn dò (2’)
- Ôn tập kỹ lý thuyết của bài đối xứng
- Giải các bài tập 60, 62, 64, 65, 66, 77/66- 67
- Đọc mục “Có thể em chưa biết” trang 89 SGK
IV RÚT KN:
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Ngày soạn 5/10/04
Tiết 12
§7. HÌNH BÌNH HÀNH
I. MỤC TIÊU:
- HS nắm được định nghĩa hình bình hành, các tính chất của hình bình hành, các dấu hiệu nhận biết một tứ giác là hình bình hành.
- HS biết vẽ hình bình hành, biết chứng minh một tứ giác là hình bình hành.
- Rèn kỹ năng suy luận, vận dụng tính chất của hình bình hành để chứng minh các đoạn thẳng, hàng, hai đường thẳng song song.
II. CHUẨN BỊ:
Thầy: Thước thẳng, compa, bảng phụ, phấn màu, một số hình vẽ, đề bài viết trên bảng phụ
Trò: Thước thẳng, compa.
III. TIẾN TRÌNH TIẾT HỌC:
1. Ổn định (1’)
2. Kiểm tra: (Không kiểm tra)
3. Bài mới:
TL
Hoạt động của thầy
Hoạt động của trò
Ghi bảng
10p
- GV đặt vấn đề: Ta đã biết đực một dạng đặc biệt của tứ giác đó là hình thang. Hãy quan sát tứ giác ABCD trên hình 66 SGK, cho biết tứ giác có gì đặc biệt? 
HS: Tứ giác ABCD có các góc kề với mỗi cạnh bù nhau
=> AB//DC, AD//BC 
- GV: Tứ giác ABCD có điểm đặc điểm như trên gọi là hình bình hành ABCD à giới thiệu bài mới. 
- GV hỏi: vậy hình bình hành là hình như thế nào?
- GV nhận xét à giới thiệu định nghĩa.
- HS trả lời..
1. Định nghĩa:
Hình bình hành là tứ giác có các cạnh đối song song
- Gọi 1 HS đọc định nghĩa SGK
- 1 HS đọc định nghĩa
B
A
C
D
- GV hướng dẫn HS vẽ hình bình hành ABCD vào vở.
- HS vẽ hình vào vở dưới sự hướng dẫn của giáo viên
- Tứ giác ABCD là hình bình hành khi nào?
- GV lưu ý: ngược lại nếu cho ABCD là hình bình hành khi ta khẳng định ngay AB//CD, AD//BC.
- Hình thang có phải là hình bình hành không?
- HS. Khi có
AB//CD, AD//BC
- HS trả lời: không phải vì hình thang chỉ có 2 cạnh đối song song
* Tứ giác ABCD là hình bình hành 
- Hình bình hành có phải là hình thang không?
- HS là một hình thang đặc biệt có hai cạnh bên song song.
* Hình bình hành là một hình thang đặc biệt.
- Hãy tìm trong thực tế hình ảnh của hình bình hành. 
- HS: khung cửa, bảng đen.
14p
- Hình bình hành là tứ giác, là hình thang, vậy trước tiên hình bình hành có những tính chất gì?
- HS.
s Tổng các góc bằng 3600
s Các góc kề mỗi cạnh bằng bù nhau.
2. Tính chất
- Hình bình hành là hình thang có 2 cạnh bên song song. Hãy thử phát biểu thêm các tính chất về cạnh, góc, đừng chéo của hình bình hành.
- HS phát hiện:
s Các cạnh đối bằng nhau.
s Hai đường chéo cắt nhau tại trung điểm của mỗi đường
- GV nhận xét, giới thiệu định lý về tính chất hình bình hành.
- Gọi HS đọc định lý SGK
- GV vẽ hình và yêu cầu HS nêu giả thiết, kết luận của định lý
- Em nào có thể chứng minh
- 1 HS trả lời miệng
Định lý: (xem SGK trang 90)
B
A
C
D
1
1
1
1
GT ABCD là hình bình 
 hành, ACÇBD={0}
KL a) AB=CD; AD=BC
 b) 
 c) OA=OC;OB=OD
Chứng minh:
- GV ghi bảng theo lời trình bày của HS, có sửa chữa cho hoàn chỉnh
a) Hình bình hành ABCD là hình thang có hai cnạh bên song song.
AD//BC nên AD = BC, AB = DC
- Em nào có thể chứng minh ý b)
- HS trả lời
b) Nối AC, xét DADC và DCBA có:
AD = BC (cmt)
DC = BA (cmt)
cạnh AC chung
=> DADC = DCBA (c – c – c) 
=> 
Chứng minh tương tự ta được
- GV nối đường chéo BD
- Gọi HS chú ý c)
c) DACB và DCOD có:
AB = CD (cmt)
so le trong do AB//DC)
=> DAOB = DCOD (g-c-g)
=> OA = OC, OD = OB 
8p
- Ta đã nắm được định nghĩa và tính chất của hình. Vậy nhờ vào dấu hiệu nào để nhận biết một hình bình hành?
- Còn có thể dựa vào dấu hiệu nào nữa không?
- GV cho HS quan sát 5 dấu hiệu nhận biết hình bình hành trên bảng phụ.
HS: Dựa vào định nghĩa tứ giác có các cạnh đối song song là hình bình hành
- HS có thể nêu tiếp 4 dấu hiệu theo SGK
- HS quan sát trên bảng phụ
s Gọi 2 HS nhận biết dáu hiệu hình bình hành.
s GV: trong 5 dấu hiệu này có 3 dấu hiệu về cạnh, 1 dấu hiệu về góc, 1 dấu hiệu về đường chéo.
s Yêu cầu HS về nhà tự chứng minh các dấu hiệu trên, xem như đây là một bài tập nhỏ
- 2 HS đọc dấu hiệu nhận biết hình bình hành.
3. Dấu hiệu nhận biết
(Xem Sgk trang 91)
?3
- Yêu cầu HS đề bài d (dề bài được ghi trên bảng phụ)	
- HS trả lời miệng.
kết quả: các tứ giác là hình bình hành: ABCD, EFGH, PQRS, XYOV
10p
Củng cố 
- Yêu cầu HS làm bài 42/92 SGK
- HS trả lời miệng:
s Các tứ giác ABCD, EFGH là các hình bình hành vì có 1 cặp cạnh đối song song và bằng nhau.
s MNPQ là hình bình hành vì có các cạnh đối bằng nhau hoặc hai đường chéo cắt nhau tại trung điểm của mỗi đường 
- Yêu cầu HS làm bài 44/92 SGK
s Gọi HS đọc đề, cho Hs quan sát hình vẽ trên bảng phụ.
- 1 HS đọc đề bài.
- HS quan sát hình vẽ trên bảng phụ
s Gọi HS nêu giả thiết, kết luận
- 1 HS ghi giả thiết, kết luận
B
A
C
D
F
E
 ABCD là hình 
GT bình hành
 AE=ED, BF=FC
KL BE=DF
s Gọi HS chứng minh BE = DF, (trả lời miệng)
HS chứng minh miệng:
ABCD là hình bình hành nếu AD = BC
Mà ED = AE = AD
BF = FC = BC
=> DE = BF
xét tứ giác DEBF có:
DE//BF (Vì AD//BC)
DF= BF (cmt)
=> DEBF là hình bình hành
=> BE = DF (Tính chất hình bình hành)
4. Dặn dò (2’)
 - Nắm vững định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành, chứng minh các dấu hiệu nhận biết.
 - Giải các bài tập 45, 46, 47 (trg 92 - 93 SGK) và bài 78, 79, 80 (SBTtrang 68)
IV RÚT KN:
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Ngày soạn 8/10/04	 TUẦN 7
Tiết 13
 LUYỆN TẬP
I. MỤC TIÊU:
- Kiểm tra, luyện tập các kiến thức về hình bình hành (định nghĩa, tính chất, dấu hiệu nhận biết).
- Rèn kỹ năng áp dụng các kiến thức trên vào giải bài tập, chú ý kỹ năng về hình, chứng minh, suy luận hợp lý.
II. CHUẨN BỊ:
Thầy: Thước thẳng, compa, bảng phụ
Trò: Thước thẳng, compa
III. TIẾN TRÌNH TIẾT DẠY:
1. Ổn định (1’)
2. Kiểm tra (7’) gọi 1 HS lên bảng
Yêu cầu:
- Phát biểu định nghĩa, tính chất hình bình hành.
- Giải bài tập 46/92 SGK
(Đáp	- Phát biểu định nghĩa, tính chất theo sách giáo khoa.
	- Bài 46/92:
a – Đúng, b – Đúng, c – Sai, d – Sai
Hỏi thêm: Tứ giác có 2đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành (Đúng).
3. Bài mới:
TL
Hoạt động của thầy
Hoạt động của trò
Ghi bảng
11p
Yêu cầu HS làm bài 47 trang 93 SGK.
- GV vẽ hình 72 lên bảng
- Gọi 1 HS viết giả thiết, kết luận.
- 1 HS đọc đề
- HS vẽ hình vào vở
- 1 HS viết giả thiết, kết luận trên bảng.
1. Bài 47/93 SGK
B
A
C
D
D
D
O
1
1
 ABCD là hình bình hành
GT AH^DB, CK^BD 
	OH=OA
KL a) AHCK là hình bình 
hành
 b) A; O; C thẳng hàng
- Quan sát hình, ta thấy ngay tứ giác AHCK có đặc điểm gì?
- HS: AH//CK vì cùng vuông góc với DB.
Chứng minh:
- Cần chỉ ra tiếp điều gì để có thể khẳng định AHCK là hình bình hành?
- Em nào có thể chứng minh được?
- HS: Cần thêm
AH = CK hoặc AH//CK
- 1 HS thực hiện
a) Theo đề bài ta có:
(1)
xét DAHD và DCKB có:
AD = CB (t/c hình bình hành)
 (So le trong của AD//BC)
=> DAHD = DCKB (ch-gn)
=>AH = CK (2)
Từ (1) và (2) => AHCK là hình bình hành.
- Ta chứng minh ý b) như thế nào? Điểm O có vị trí như thế nào đối với đoạn thảng HK?
- HS trả lời miệng
b) Ta có: O là trung điểm của HK mà AHCK là hình bình hành (chứng minh a)
=> O là trung điểm của đường chéo AC (tính chất của hình bình hành)
=> A, O, C thẳng hàng 
10p
Yêu cầu HS làm bài 48 trang 92 SGK
A
H
D
B
F
G
C
E
2. Bài 48/92 SGK 
- Gọi HS đọc đề bài
- 1 HS đọc đề bài 
- Gọi HS vẽ hình, ghi giả thiết, kết luận
- 1HS vẽ hình, ghi giả thiết, kết luận cả lớp thực hiện vào vở.
- HEFG là hình gì? Vì sao
HS: HEFG là hình bình hành (có thể chưa giải thích được ngay)
ABCD, AE=EB,
GT	BF=FC, CG=GD
DH=DA
KL	HEFG là hình gì? 
vì sao
- GV: H, E là trung điểm của AD, AB. Vậy có kết luận gì về đoạn thẳng HE
- HS: HE là đường trung bình cả DADB
Giải:
Theo đề bài: H, E, F, G lần lượt là trung điểm của AD, AB, CB, CD
- GV: Tương tự đối với đoạn thẳng GF?
- HS trả lời..
=> HE và FG lần lượt là đường trung bình của DADB và DDBC
s Gọi 1 HS thực hiện 
- 1 HS thực hiện
Nên:
- Gọi HS nhận xét phần trình bày của bạn
- HS nhận xét bài giải
HE//DB và HE = DB
GF//DB và GF = DB
=> HE//GF và HE = GF 
- GV: còn cách chứng minh nào khác? Các em về nhà tiếp tục tìm hiểu
=> Tứ giác EFGH là hình bình hành.
14p
Yêu cầu HS quan sát đề bài trên bảng?
Đề: Cho hình bình hành ABCD, qua B vẽ đoạn thẳng EF sao cho EF//AC và EB = BF = AC
a) Các tứ giác AEBC, ABFC là hình gì?
b) Hình bình hành ABCD có thêm điều kiện gì thì E đối xứng với F qua đường thẳng BD?
E
A
B
F
C
D
- Gọi HS đọc đề
- Gọi HS vẽ hình, ghi giả thiết, kết luận 
- 1 HS đọc đề
- 1 HS vẽ hình, ghi giả thiết, kết luận, cả lớp thực hiện vào vở.
ABCD là hình gì?
GT	BÎEF, EF//AC,
BE=BF=AC
a) AEBC? ABFC?
KL	b) điều kiện để E đối 
xứng với F qua BD
- Em nào thực hiện câu a
- 1 HS lên bảng thực hiện.
Giải:
a) Tứ giác AEBC là hình bình hành vì EB//AC và EB = AC (gt)
Tứ giác ABFC là hình bình hành vì BF//AC và BF = AC (gt)
- Khi nào thì 2 điểm là đối xứng với nhau qua một đường thẳng?
- HS: 2 điểm. khi đường thẳng là đường trung trực của đoạn thẳng nối 2 điểm đó.
- Vậy E và F đối xứng qua BD khi nào?
- HS.
b) E và F đối xứng với nhau qua dường thẳng BD BD là đường trung trực của đoạn thẳng EF.
)
EF//AC)
 DDAC cân tại O vì có DO vừa là trung tuyến, vừa là đường cao.
- GV hướng dẫn HS trình bày.
- HS trình bày theo hướng dẫn của GV
E
A
B
F
C
D
 Hình bình hành ABCD có hai cạnh kế bằng nhau.
4. Dặn dò (2’)
- Cần nắm vững và phân biệt được định nghĩa, tính chất, dấu hiệu nhận biết hình.
- Làm các bài tập 49/93 SGK và 83, 85, 87, 89/69 SBT.
IV RÚT KN:
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Ngày soạn 11/10/04
Tiết 14
§8. ĐỐI XỨNG TÂM
I. MỤC TIÊU:
- HS hiểu được các định nghĩa hai điểm đối xứng nhau qua một điểm, hai hình đối xứng qua một điểm, hình có tâm đối xứng.
- HS biết vẽ hình đối xứng với một điểm cho trước, đoạn thẳng đối xứng với một đoạn thẳng trước qua một điểm.
- HS biết chứng minh hai điểm đối xứng với nhau qua một điểm.
- HS nhận ra một số hình có tâm đối xứng trong thực tế.
II. CHUẨN BỊ: 
Thầy: Thước thẳng, compa, phóng to hình 78 và một vài chữ (N, S, E) trên bảng phụ, phấn màu.
Trò: Thước thẳng, compa, giấy kẻ ô vuông
III. TIẾN TRÌNH TIẾT DẠY
1. Ổn định (1’)
2. Kiểm tra (5’) gọi 1 HS lên bảng.
- Phát biểu định nghĩa hình bình hành, dấu hiệu nhận biết hình bình hành.
- Vẽ hình bình hành, nêu tính chất hai dường chéo của hình bình hành.
GV nhẫn ét, ghi điểm
GV giới thiệu: A và C gọi là đối xứng nhau qua O
à Giới thiệu bài mới
3. Bài mới
TL
Hoạt động của thầy
Hoạt động của trò
Ghi bảng
7p
Yêu cầu thực hiện 
- GV giới thiệu: A’ là điểm đốI xứng vớI A qua O, A là điểm đốI xứng với A’ là hai điểm đối xứng với nhau qua điểm O
- HS làm vào vở 1 HS lên bảng vẽ
1. Hai điểm đối xứng qua một điểm
 A	 B C
- Thế nào là 2 điểm đối xứng với nhau qua điểm O?
- HS  nếu O là trung điểm của đoạn thẳng nối 2 điểm đó.
- GV giới thiệu định nghĩa, gọi HS đọc định nghĩa SGK
- HS đọc định nghĩa
** Định nghĩa
- Nếu A º O thì A’ ở đâu?
- HS: Nếu A º O thì A’ º O
(Xem SGK trang 93)
- GV nêu quy ước.
** Quy ước 
- Quay lại hình vẽ ở phần kiểm tra, hãy tìm các cặp điểm đối xứng với nhau qua giao điểm của hai đường chéo.
- HS A và C, B và D 
(Xem SGK trang 93)
- Với 1 điểm O cho trước, ứng với 1 điểm A có bao nhiêu điểm đối xứng với A qua điểm O?
- HS:. chỉ có một điểm đối xứng với A qua điểm O
13p
?2
Yêu cầu HS thực hiện 
- GV vẽ trên bảng đoạn thẳng AB và điểm O, yêu cầu HS thực hiện từng yêu cầu của đề bài 
- HS vẽ hình vào vở, 1 HS lên bảng thực hiện 
- GV: 2 đoạn thẳng AB và A’B’ trên hình là hai đoạn thẳng đối xứng với nhau qua O, còn gọi là hai hình đối xứng với 1 điểm thuộc đoạn A’B’ qua điểm O và ngược lại. Vậy thế nào là 2 hình đối xứng với nhau qua điểm O. 
HS nêu định nghĩa đối xứng với nhau qua điểm O như SGK.
A
A
A
O
B’
C’
A’
2. Hai hình đối xứng nhau qua một điểm: 
- GV đọc định nghĩa và giới thiệu điểm O gọi là tâm đối xứng của 2 hình đó.
Trên hình vẽ: 2 đoạn thẳng AB và A’B’ gọi là hai đoạn thẳng đối xứng nhau qua điểm O
- GV sử dụng hình 77 phóng to để giới thiệu về 2 đoạn thẳng, 2 đường thẳng, 2 góc, 2 tam giác đối xứng nhau qua tâm O.
** Định nghĩa:
Xem SGK trang 94 
- Có nhận xét gì về 2 đoạn thẳng (góc, tam giác) xứng với nhau qua 1 điểm. 
- HS chúng bằng nhau
** Người ta đã chứng minh được rằng.
- GV khẳng định nhận xét à giới thiệu định nghĩa
Nếu hai đoạn thẳng (góc, tam giác) đối 
- Quan sát hình 78 SGK, cho biết H và H’ có quan hệ gì?
- HS: Hai hình H và H’ đối xứng nhau qua tâm O
xứng với nhau qua một điểm thì chúng bằng nhau 
- Nếu quay hình H quanh O một góc 1800 thì sao?
- HS thì 2 hình trùng nhau 
9p
- GV sử dụng hình bình hành ở phần kiểm tra:
3. Hình có tâm đối xứng
s Ở hình bình hành ABCD, hãy tìm hình đối xứng của cạnh AB, của cạnh AD qua tâm O? 
- HS: Hình đối xứng với AB và CD qua tâm O lần B
A
C
D
O
lượt là cạnh CD và cạnh BC.
s Điểm đối xứng qua tâm O với điểm M bất kỳ thuộc hình bình hành ABCD ở đâu? (GV lấy điểm M thuộc cạnh của hình bình hành ABCD).
- HS: Điểm đối xứng với điểm M qua tâm O cùng thuộc hình bình hành ABCD.
Giao điểm O của hai đường chéo trong hình bình hành ABCD là tâm đối xứng của hình bình hành ABCD.
s Gọi HS vẽ điểm M’ đối xứng với M qua O.
- HS: Vẽ điểm M’ đối xứng với M qua O
* Định nghĩa:
Xem SGK trang 95
- GV giới thiệu: điểm O là tâm đối xứng của hình bình hành ABCD và nêu tổng quát, định nghĩa tâm đối xứng của hình H trang 95 SGK.
- GV yêu cầu HS đọc định lý SGK
- 1 HS đọc đúng định lý trang 95 SGK
* Định lý
Xem SGK trang 95
?3
- Cho HS làm 
- HS trả lời miệng
8P
Củng cố:
- GV sử dụng các hình tâm giác đều, hình bình hành, đường tròn, hình thang cân, các chữ cái M, H, I; cho HS quan sát và hỏi: Trong các hình trên, hình nào có tâm đối xứng? Có mấy trục?
HS làm việc theo nhóm.
+ Chữ M: không có tâm đối xứng, có một trục đối xứng.
+ Chữ H: có một tâm đối xứng, 2 trục đối xứng.
+ Chữ I: có 1 tâm đối xứng, 2 trục đối xứng.
+Tam giác đều không có không có tâm đối xứng, 3 trục đối xứng.
+ Hình thang cân có 1 trục đối xứng, không có tâm đối xứng.
+ Đường tròn có 1 tâm đối xứng, có vô số trục đối xứng.
+ Hình bình hành có 1 tâm đối xứng, không có trục đối xứng.
- GV nhận xét và giải thích rõ hơn
Đại diện 1 nhóm trình bày.
4. Dặn dò (2’)
- Nắm vững định nghĩa 2 điểm đối xứng qua 1 điểm, 2 hình đối xứng qua 1 tâm, hình có tâm đối xứng.
- So sánh với phép đối xứng qua trục.
- Giải các bài tập 50, 52, 53, 56 trang 69 SGK – bài 92, 93, 94 trang 70 SBT.
IV RÚT KN:
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................