Giáo án môn Đại số 8 - Tuần 36 (Bản đẹp)

Tuần: 36
Tiết: 70
Ngày soạn: 
Ngày dạy: 
Lớp: 8/1 + 8/2
KIỂM TRA HỌC KÌ II
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II
MÔN: TOÁN 8
(Thời gian 90 phút, không kể phát đề)
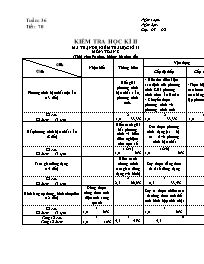
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Phương trình bậc nhất một ẩn 
(13 tiết)
Biết giải phương trình bậc nhất 1 ẩn, phương trình tích. 
- Biết tìm điều kiện xác định của phương trình Giải phương trình chứa ẩn ở mẫu
- Chuyển được phương trình về phương trình tích
- Thực hiện đúng các bước giải bài toán bằng cách lập phương trình
Số câu
Số điểm Tỉ lệ %
2
 1,0 33,3%
2
1,0 33,3%
1
 1,0 33,3%
5
3,0 điểm= 30%
Bất phương trình bậc nhất 1 ẩn
 (8 tiết)
Hiểu cách giải bất phương trình và biểu diễn nghiệm trên trục số
Đưa được phương trình dạng |ax + b| = cx + d về phương trình bậc nhất
Số câu
Số điểm Tỉ lệ %
1 (2-a)
1,0 50%
1 (2-b)
1,0 50%
2
2,0 điểm= 20%
Tam giác đồng dạng
(14 tiết)
Hiểu cách chứng minh tam giác đồng dạng (vẽ hình)
Suy được đẳng thức từ tỉ số đồng dạng
Số câu
Số điểm Tỉ lệ %
2
2,5 66,6%
1
0,5 33,4 %
3
3,0 điểm= 30%
Hình lăng trụ đứng, hình chóp đều (12 tiết)
Dùng được công thức tính diện tích xung quanh
Suy ra được chiều cao từ công thức tính thể tích hình hộp chữ nhật
Số câu
Số điểm Tỉ lệ %
1
1,0 50%
1
1,0 50%
2
2,0 điểm= 20%
Tổng số câu
Tổng số điểm
1
1,0 10%
5
4,5 45%
6
 4,5 45%
12
10 điểm
ĐỀ KIỂM TRA HỌC KÌ II
MÔN: TOÁN 8
Năm học: 2010 – 2011
(Thời gian 90 phút, không kể phát đề)
Câu 1(2đ): Giải các phương trình
a. x + 3 = 0 
b. (x – 1)(2x – 1) = 0
c. 
d. x2 – 2x + 2 – x = 0
Câu 2( 2đ)
a. Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số
3x + 6 > 0
b. Giải phương trình: |x – 1| = x – 5
Câu 3(1đ): Một người đi xe máy từ A đến B với vận tốc 30 km/h. Khi đến B người đó nghỉ tại B 1 giờ rồi quay về A với vận tốc 24 km/h. Biết tổng thời gian từ lúc đi đến khi về đến A hết 5 giờ 30 phút. Tính quãng đường AB ?
Câu 4(3đ): Cho tam giác ABC vuông tại A, biết AB = 4cm, AC = 3cm. Kẻ đường cao AH ( H nằm trên BC).
S
a. Chứng minh ACH = BAH
b. Chứng minh DAHB DCHA
	c. Chứng minh AH.BC = AB.AC
Câu 5(2đ): Một bể nước hình hộp chữ nhật có chiều dài là 2m, rộng 1,2m, cao 1m. 
2m
1,2m
1m
a. Tính diện tích xung quanh của bể nước
	b. Người ta đổ vào bể 0,6 m3 nước thì nước trong bể cao bao nhiêu cm ? 
ĐÁP ÁN ĐỀ KIỂM TRA TOÁN 8 – HK II
NĂM HỌC: 2010 – 2011
Bài
Đáp án
Điểm
Bài 1
(2đ)
a. x + 3 = 0 x = -3
0,5đ
b. (x – 1)(2x – 1) = 0 => x – 1 = 0 hoặc 2x – 1 = 0
 * x – 1 = 0 x = 1
 * 2x – 1 = 0 x = 
0,25đ
0,25đ
c. * ĐKXĐ: x 2
Ta có: 1 + 3(x – 2) = 4 3x = 9 
 x = 3 (thỏa mãn)
Vậy phương trình có nghiệm x = 3
0,25đ
0,25đ
d. x2 - 2x + 2 – x = 0 x(x-2) - (x-2) = 0 
 (x-2)(x-1) = 0 x - 2 = 0 hoặc x - 1 = 0
* x – 2 = 0 x = 2 
* x – 1 = 0 x = 1 
Tập nghiệm của phương trình: S = {2; 1}
0,25đ
0,25đ
Bài 2
(2đ)
a. 3x + 6 > 0 x > -2
(
0
-2
0,5đ
0,5đ
b. * Xét trường hợp x 1, ta có phương trình: 
x – 1= x – 5 0x = -4 ( vô nghiệm)
* Xét trường hợp x < 1, ta có phương trình: 
1 – x = x – 5 2x = 6 x = 3 (loại)
Vậy phương trình đã cho vô nghiệm
0,25đ
0,25đ
0,5đ
Bài 3
(1đ)
Đổi 5h30’ = 5,5h
Gọi x là độ dài quãng đường AB ( x > 0, km)
Thời gian người đó đi từ A đến B là: (h)
Thời gian người đó đi từ B về A là: (h)
 Do nghỉ tại B 1h, người đó mới trở về A, ta có phương trình: 
+ + 1 = 5,5
Giải phương trình được x = 60 ( thỏa mãn điều kiện) 
A
C
B
H
Vậy quãng đường AB dài 60 km
1đ
Bài 4
(3đ)
0,5đ
a. Ta có: ACH + ABH = 900 ( hai góc phụ nhau) (1)
 Lại có: HAB + ABH = 900 (hai góc phụ nhau) (2)
 Từ (1) và (2) => ACH = HAB (đpcm) 
1đ
b. Xét hai DAHB và DCHA có: 
ACH = HAB (cm trên)
S
AHB = CHA = 900
Vậy DAHB DCHA (g.g)
1đ
c. Xét hai DAHC và DABC có: 
C chung 
S
BAC = AHC = 900
Vậy DAHC DBAC (g.g) 
=> => AH.BC = AB.AC (đpcm)
0,5đ
Bài 5
(2đ)
a. Diện tích toàn phần của bể nước là: 
Stp = 2(2 + 1,2).1 = 6,4 m2
1đ
b. Gọi chiều cao của mực nước là x, ta có: 
Vnước = 2.1,2.x => 2,4.x = 0,6 x = 0,25 m = 25 cm
1đ