Giáo án Hình học Khối 9 - Chương 1: Hệ thức lượng trong tam giác vuông
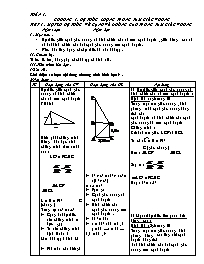
/ Hệ thức giữa cạnh góc vuông và
hình chiếu của nó trên cạnh huyền :
Định lí 1 : sgk trang 65
Trong một tam giác vuông , bình phương mỗi cạnh góc vuông bằng tích của
cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền
Chứng minh :
Xét hai tam giác ACB và HCA
Ta có : A = H = 900
C ( góc chung )
Nên : ACB HCA
Suy ra :
AC2 = BC.HC
Hay : b2 = a.b/
2/ Một số hệ thức liên quan đến đường cao :
Định lí 2 : Sgk trang 65
Trong một tam giác vuông bình phương đường cao ứng với cạnh huyền bằng tích
hai hình chiếu của hai cạnh góc vuông trên cạnh huyền
h2 = b/.c/
học sinh tự ghi chứng minh
Ví dụ 2 : Xem sách giáo khoa
Bài tập 2 hình 5
Ta có : x2 = 1( 1 + 4 ) = 5
Suy ra : x =
Tương tự ta có : y2 = 4 ( 1 + 4 ) = 20
Suy ra : y =
Bạn đang xem 20 trang mẫu của tài liệu "Giáo án Hình học Khối 9 - Chương 1: Hệ thức lượng trong tam giác vuông", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
TUẦN 1. CHƯƠNG I : HỆ THỨC LƯỢNG TRONG TAM GIÁC VUễNG TIẾT 1 : MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUễNG Ngày soạn Ngày dạy I . Mục tiờu : Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền , giữa đường cao và và hai hình chiếu của hai cạnh góc vuông trên cạnh huyền. Bước đầu ứng dụng các hệ thức đó vào bài tập . II. Chuẩn bị : Thước E- ke , bảng phụ các bài tập có hình vẽ . III. Tiến trỡnh bài dạy : 1/Bài cũ : Giới thiệu sơ lược nội dung chương trỡnh hỡnh học 9 . 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền Vẽ hình Điều phải chứng minh Hướng dẫn học sinh chứng minh theo sơ đồ sau : AC2 = BC.HC ACB HCA A = H = 900 C (chung ) Tương tự : c2 = a.c/ Cộng hai hệ thức vừa chứng minh ta được gì ? Ta vừa chứng minh dịnh lí nào ? Làm bài tập 1 hình 4b Bài toán cho biết gì ? x , y là yếu tố gì trong hình ? Viết công thức liên hệ giữa x , và các yếu tố liên quan ? Tìm x , y ? Hoạt động 2 : Một số hệ thức liên quan đến đường cao : Nêu định lí 2 Phân tích và hướng dẫn chứng minh như trên Nêu ví dụ 2 : Ta thấy những đoạn thẳng nào bằng 1,5 m và 2,25 trừ DE và AE ? Bài toán tìm gì ? áp dụng công thức nào ? b2 + c2 = ab/ + ac/ = a(b/ + c/ ) = a.a = a2 Pyta go Cạnh góc vuông và cạnh huyền Hình chiếu của cạnh góc vuông trên cạnh huyền . 122 = 20x x = 122 : 20 = 7 , 2 y = 20 –x = 20 –7,2 = 12 , 8 AB = 1,5 m và BD = 2 , 25 Chiều cao của cây , tức là AC BD2 = AB . BC Hai hình chiếu của 2 cạnh góc vuông Hai cạnh góc vuông AB2 = BC .BH 1 + 4 x2 = 1( 1 + 4 ) = 5 y2 = 4 ( 1 + 4 ) = 20 x = , y = 1/ Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền : Định lí 1 : sgk trang 65 Trong một tam giác vuông , bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền Chứng minh : Xét hai tam giác ACB và HCA Ta có : A = H = 900 C ( góc chung ) Nên : ACB HCA Suy ra : AC2 = BC.HC Hay : b2 = a.b/ 2/ Một số hệ thức liên quan đến đường cao : Định lí 2 : Sgk trang 65 Trong một tam giác vuông bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền h2 = b/.c/ học sinh tự ghi chứng minh Ví dụ 2 : Xem sách giáo khoa Bài tập 2 hình 5 Ta có : x2 = 1( 1 + 4 ) = 5 Suy ra : x = Tương tự ta có : y2 = 4 ( 1 + 4 ) = 20 Suy ra : y = IV. Luyện tập - Củng cố : Bài tập 2 hình 5 Cho biết những yếu tố nào ? Yếu tố cần tìm ? Công thức tính cạnh góc vuông ? BC = ? Ta có : Suy ra :x ? y ? V . Hướng dẫn về nhà : Về nhà học thuộc 2 định lí , công thức biểu thị , làm bài tập 1 hình 4a , Bài tập 5 SGK trang 69 VI. Rỳt kinh nghiệm : TUẦN 2 . TIẾT 2 : MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUễNG Ngày soạn Ngày dạy I . Mục tiờu : + Hệ thức giữa dường cao với cạnh huyền và hai cạnh góc vuông , giữa đường cao và hai cạnh góc vuông . + Bước đầu ứng dụng các hệ thức đó vào bài tập . II. Chuẩn bị : Thước E- ke , bảng phụ các bài tập có hình vẽ . III. Tiến trỡnh bài dạy : 1/Bài cũ : 1/ Phát biểu định lí về hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền . 2/ Phát biểu định lí về hệ thức giữa đường cao với hai hình chiếu của hai cạnh góc vuông . Sửa bài tập 1 hình 4a Bài tập 5 trang 69 . Trong tạm giác vuông với các cạnh góc vuông là 3 và 4 , kẻ đường cao ứng với cạnh huyền . Hãy tính đường cao này và các độ dài các đoạn thẳng mà nó địnhk ra trên cạnh huyền +Vẽ hình , đặt tên cho các yếu tố của hình . ( Giả sử tam giác ABC vuông tại A có AB = 3 , BC = 4 , đường cao ứng với cạnh huyền là AH ) +Tính độ dài những đoạn thẳng nào ? ( AH , BH , HC ) 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung S Hệ thức giữa đường cao với cạnh huyền với cạnh huyền và hai cạnh góc vuông . +Nêu định lí 3 Điều phải chứng minh ? Hướng dẫn phân tích : AB.AC = BC . AH ABC HAC Ngoài ra ta còn chứng minh định lí này bằng công thức tính diện tích như sau : Tích bc là gì của tam giác vuông ABC ? Tích ah là gì của tam giác vuông ABC ? Suy ra điều gì ? Hệ thức giữa đường cao và hai cạnh góc vuông . Từ ah = bc ta có thể suy ra mối quan hệ giữa đường cao và hai cạnh góc vuông . Ta thay a bằng b và c bằng công thức nào ? Ta có gì ? -Biến đổi đẳng thức đó thành một tỉ lệ thức Từ viết thành tổng hai phân số +Nêu định lí 4 . x + y = = = 10 62 = 10.x x = 62 : 10 = 3,6 y = 10 – x = 10 –3,6 = 6,4 Tam giác ABC vuông tại A , đường cao AH . Ta có : BC = = 5 Và : AB2 = BH.BC BH = CH = BC –BH = 5 –1,8 = 3 ,2 Định lí 3 : Sgk trang 65 Trong một tam giác vuông , tích hai cạnh góc vuông bằng tích cạnh huyền và đường cao tương ứng . ah = bc Chứng minh : Xét ABC và HAC Có : BAC = AHC = 900 ABC = HAC ( cùng phụ với góc C ) Do đó : ABC HAC Suy ra : AB.AC = BC . AH Hay : bc = ah Định lí 4 : Sgk trang 67 Trong một tam giác vuông , nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông . IV. Luyện tập - Củng cố : Bài tập 3 hình 6 trang 69 Cho biết gì ? Tìm gì ? Tìm đoạn thẳng nào trước vì sao ? Dùng công thức nào ? Nếu tìm x trước ta dùng công thức nào ? Diện tích của tam giác vuông ABC Diện tích của tam giác vuông ABC ah = bc a2 = b2 + c2 (b2 + c2 )h2 = b2c2 = Hai cạnh góc vuông . Đường cao và cạnh huyền . Cạnh huyền vì đã biết hai cạnh góc vuông . y = xy = 5.7 x = V . Hướng dẫn về nhà : Làm bài tập 4 , 6 , 7 sgk trang 69 Xem phần có thể em chưa biết để giải thích bài tập 7 VI. Rỳt kinh nghiệm : TUẦN 3 . TIẾT 3-4 : LUYỆN TẬP Ngày soạn Ngày dạy I . Mục tiờu : + Vận dụng 4 hệ thức trên để giải bài tập , Rèn luyện kĩ năng tính toán , biến đổi công thức , chứng minh . + Nắm được cách dựng đoạn trung bình nhân của hai đoạn thẳng . II. Chuẩn bị : Thước E- ke , bảng phụ các bài tập có hình vẽ . III. Tiến trỡnh bài dạy : 1/Bài cũ : 1/ Gọi 4 học sinh phát biểu 4 định lí 2/ Gọi 2 học sinh lên bảng sửa bài tập 4 và 6 Bài tập 4 trang 69 22 = 1.x x = 4 y = Bài tập 6 trang 69 BC = BH + HC = 1 + 2 = 3 AB2 = BH . BC = 1.3 = 3 AB = 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung . Hướng dẫn sửa bài tập 7 Trên 1 đường thẳng dựng đoạn BH = a và HC = b ( H nằm giữa B và C ) Dựng nửa đường tròn tâm O đường kính BC . Qua H vễ đường thẳng vuông góc với BC cắt nửa đường tròn ( O ) tại A . AH là đọn thẳng x cần dựng thoả mản x2 = a.b Chứng tỏ x2 = a.b hay AH2 = BH.HC Ta cần tìm gì ? Căn cứ ? Tương tự : BH = a , BC = b Thì AB là đoạn cần dựng . Bài tập 8b trang 70 Tam giác vuông có gì đặc biệt ? Tìm được gì ? vì sao ? Bài tập 9 trang 70 Cho hình vuông ABCD . Gọi I là một điểm nằm giữa A và B . Tia DI và tia CB cắt nhau ở K . Kẻ đường thẳng qua D , vuông góc với DI . Đường thẳng này cắt đường thẳng BC tại L Chứng minh rằng : Tam giác DIL là tam giác cân . Tổng không thay đổi khi I thay đổi trên cạnh AB . a) Hướng dẫn đến sơ đồ sau : DIL cân DI = DL ADI = CDL AD = CD ADI = CDL b) Trong hình có những đại lượng nào không đổi ? Tổng gợi cho chúng ta nhớ tới hệ thức nào ? Xem xét các cạnh AB , BC , CD , DA thì cạnh nào là đường cao của một tam giác vuông có cạnh góc vuông là DI hoặc DL Cạnh góc vuông kia là gì ? Suy ra điều cần tìm ? Tam giác ABC vuông tại A Trung tuyến ứng với với một cạnh bằng nửa cạnh đó . Tam giác vuông cân , vì hai cạnh góc vuông bằng nhau ( cùng bằng y ) Tìm được x vì trung tuyến ứng với cạnh huyền . x = 2 y = AB , BC , CD , DA Giữa đường cao và hai cạnh góc vuông . DC là đường cao của tam giác vuông DLK có cạnh góc vuông là DK DL DI = DL Bài tập 7 : Xét tam giác ABC Có OB = OC Nên AO là trung tuyến ứng với cạnh BC . Mà AO = BC Nên tam giác ABC vuông tại A có AH là đường cao . Vì Vậy : AH2 = BH.HC hay x2 = a.b Xét ADI và CDL Có A = C = 900 AD = CD ADI = CDL Do đó : ADI = CDL ( g . c . g ) Suy ra : DI = DL Nên DIL cân Tam giác DLK vuông tại D , có DC là đường cao . Ta có : Mà DI = DL ( cmt ) Suy ra : ( không đổi ) Hay : Tổng không thay đổi khi I thay đổi trên cạnh AB IV. Luyện tập - Củng cố : V . Hướng dẫn về nhà : Làm bài tập 8a , 8c trang 70 , xem lại cách viết các hệ thức tỉ lệ giữa các cạnh của hai tam giác đồng dạng VI. Rỳt kinh nghiệm : TIẾT 5 : TỈ SỐ LƯỢNG GIÁC CỦA GểC NHỌN Ngày soạn Ngày dạy I . Mục tiờu : Nắm vững các công thức định nghĩa các tỉ số lượng giác của một góc nhọn và ý nghĩa của các tỉ số này chỉ phụ thuộc vào độ lớn của góc nhọn . II. Chuẩn bị : Thước E- ke , bảng phụ các bài tập có hình vẽ . III. Tiến trỡnh bài dạy : 1/Bài cũ : 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung Khái niệm tỉ số lượng giác của một góc nhọn . Cho hai tam giác vuông ABC và A/B/C/ có góc nhọn B = B/ = Hai tam giác vuông đó có đồng dạng với nhau hay không ? vì sao ? Viết các hệ thức tỉ lệ giứa các cạnh của chung . Như Vậy : Với mọi tam giác vuông có cùng một góc nhọn thì các tỉ số ở trên như thế nào ? Nghĩa là ? ?1 qua bảng phụ sau : Hãy điền vào chỗ trống ( ... ) ở bảng sau : Cho tam giác ABC vuông tại A có B = Khi B = = 450 Thì tam giác ABC ... Do đó : AB = AC Vậy : = .... Ngược lại : nếu = .... Thì .... Nên tam giác ABC ... Suy ra B = = ... Khi B = = 600 Thì tam giác ABC là một ... Nên BC = 2..... Suy ra AC = ... Nên : = ... Ngược lại : nếu = Suy ra AC = ...AB Thì BC = ... Nên tam giác ABC là ... Suy ra B = = ... Qua bài trên ta thấy : Với góc nhọn xác định thì tỉ số như thế nào ? và ngược lại . Nếu độ lớn góc thay đổi thì tỉ số có thay đổi không ? Tương tự các tỉ số Vậy : Trong một tam giác vuông , các tỉ số trên như thế nào ? Trong tam giác ABC vuông tại A , người ta quy ước : Với góc nhọn B thì AB gọi là cạnh kề , AC gọi là cạnh đối . Các tỉ số trên gọi là tỉ số lượng giác của góc B . Giới thiệu tên gọi các tỉ số lượng giác , kí hiệu . Độ dài các cạnh của tam giác nhận giá trị gì ? Suy ra các tỉ số lượng giác của một góc nhọn nhận giá trị như thế nào ? So sánh cạnh đối với cạnh huyền , cạnh kề với cạnh huyền ? Suy ra sin , cos có đặc điểm gì ? Nêu nhận xét . Làm ? 2 Cho tam giác ABC vuông tại A có C = . Hãy viết các tỉ số lượng giác của góc . Đồng dạng với nhau , trường hợp góc – góc . ; ; ; bằng nhau . Không thay đổi Cho tam giác ABC vuông tại A có B = Khi B = = 450 Thì tam giác ABC vuông cân tại A Do đó : AB = AC Vậy : = 1 Ngược lại : nếu = 1 Thì AB = AC Nên tam giác ABC vuông cân tại A Suy ra B = = 450 Khi B = = 600 Thì tam giác ABC là một nửa tam giác đều Nên BC = 2.AB Suy ra AC = = Nên : = Ngược lại : nế ... Vẽ DH vuông góc với AB , ta có tam giác ADH vuông tại H . Nên : DH = AD.sinA Mà : : SABCD = AB.DH Suy ra : : SABCD = AB.AD.sinA BÀI TẬP : Cho tam giỏc ABC cú AB = 3 ; AC = 6 ; A = 1200 . Tớnh độ dài phõn giỏc AD . Giải : Ta cú : IV. Luyện tập - Củng cố : V . Hướng dẫn về nhà : Về nhà làm bài tập 32 SGK trang 89 , tính diện tích một hình thang nếu biết hai đáy và 1 góc , 1 cạnh bên . Xem trước và chuẩn bị dụng cụ cho bài sau . VI. Rỳt kinh nghiệm : TUẦN 8 . TIẾT 15: ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GểC NHỌN . THỰC HÀNH NGOÀI TRỜI Ngày soạn Ngày dạy I . Mục tiờu : Biét xác định chiều cao của vật thể mà không cần lên điểm cao nhất của nó . Rèn luyện kĩ năng đo đạt trong thực tế , rèn luyện ý thức làm việc tập thể II. Chuẩn bị : Bảng VIII , IX , X của bảng số có 4 chữ số thập phân ..MTBT , dụng cụ thực hành . III. Tiến trỡnh bài dạy : 1/ Xác định chiều cao : Nêu nhiệm vụ và hướng dẫn thực hiện Nhiệm vụ : Xác định chiều cao của cột cờ trường mà không cần lên đến đỉnh cột cờ Hướng dẫn thực hiện : Treo bảng phụ có hình vẽ như hình 34 Nêu câu hỏi : Vì sao b + atg là chiều cao của cột cờ ? Hướng dẫn thực hiện : Đặt giác kế thẳng đứng cách chân cột cờ một khoảng cách a ( đo a ) Đo chiều cao giác kế b Quay giác kế sao cho khi ngắm theo thanh này ta nhìn thấy đỉnh A của cột cờ , Xác định góc Tính b + atg Thực hành Thực hành : Chia tổ , thực hành 3 lần , mỗi lần với khoảng cách a khác nhau . Bản báo cáo thực hành : Kiểm tra , đánh giá : Chuẩn bị dụng cụ : 2 điểm í thức kỉ luật : 3 điểm Kết quả thực hành : 5 điểm . V . Hướng dẫn về nhà :Xem trước phần xác định khoảng cách và chuẩn bị dụng cụ cho tiết thực hành sau . VI. Rỳt kinh nghiệm : TIẾT 16 : ỨNG DỤNG THỰC TẾ CÁC TỈ SỐ LƯỢNG GIÁC CỦA GểC NHỌN . THỰC HÀNH NGOÀI TRỜI Ngày soạn Ngày dạy I . Mục tiờu : Biét xác định khoảng cách giữa hai địa điểm , trong đó có một địa điểm khó tới được . Rèn luyện kĩ năng đo đạt trong thực tế , rèn luyện ý thức làm việc tập thể II. Chuẩn bị : Bảng VIII , IX , X của bảng số có 4 chữ số thập phân ..MTBT , dụng cụ thực hành . III. Tiến trỡnh bài dạy : 2/Nội dung : 1/ Xác định khoảng cách : Nêu nhiệm vụ và hướng dẫn thực hiện Nhiệm vụ : Xác định chiều rộng của cái hồ cá Bác Hồ cạnh trường Nêu câu hỏi : Vì sao atg là chiều rộng của hồ ? Hướng dẫn thực hiện : Chọn một điểm B bên kia hồ Lấy một điểm A bên này hồ sao cho AB vuông góc với 2 bờ hồ Dùng E ke đạt kẻ đường thẳng Ax sao cho Ax vuông góc với AB , trên Ax lấy điểm C sao cho AC = a Dùng giác kế đo góc ACB = Tính atg Thực hành Thực hành : Chia tổ , thực hành 3 lần , mỗi lần với khoảng cách a khác nhau . Bản báo cáo thực hành : Kiểm tra , đánh giá : Chuẩn bị dụng cụ : 2 điểm í thức kỉ luật : 3 điểm Kết quả thực hành : 5 điểm . V . Hướng dẫn về nhà : Trả lời các câu hỏi 1 , 2 , 3 .4 trang 91 . 92 . Ôn lại kiến thức của chương ở phần tóm tắc kiến thức . làm bài tập 33 , 34 trang 93 , 94 VI. Rỳt kinh nghiệm : TUẦN 9 . TIẾT 17 : ễN TẬP CHƯƠNG I Ngày soạn Ngày dạy I . Mục tiờu : + Hệ thống hoỏ cỏc hệ thức về cạnh và đường cao trong tam giỏc vuụng . + Hệ thống hoỏ cỏc cụng thức định nghĩa cỏc tỉ số lượng giỏc của một gúc nhọn và quan hệ giữa cỏc tỉ số lượng giỏc của hai gúc phụ nhau . + Rốn luyện kĩ năng tra bảng , sử dụng mỏy tớnh bỏ tỳi để tớnh cỏc tỉ số lượng giỏc , tớnh số đo gúc . II. Chuẩn bị : Thước kẻ . Compa . MTBT . Bảng tỉ số lượng giỏc . Bảng phụ . III. Tiến trỡnh bài dạy : 1/Bài cũ : 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung Cho hình 36 . Hãy viết hệ thức giữa : Cạnh huyền , cạnh góc vuông và hình chiếu của nó trên cạnh huyền . Các cạnh góc vuông và đường cao Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền 2/ Cho hình 37 Hãy viết công thức tính các tỉ số lượng giác của góc . Hãy viết hệ thức giữa các tỉ số lượng giác của góc và các tỉ số lượng giác của góc . 3/Xem hình 37 Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc và Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc và 4/ Để giải một tam giác vuông cần biết ít nhất mấy góc và cạnh ? có lưu ý gì về số cạnh ? Bài tập trắc nghiệm củng cố về tỉ số lượng giác của góc nhọn , của góc đặc biệt , hệ thức về tỉ số lượng giác của hai góc phụ nhau Bài tập 33 , 34 SGK trang 93 , 94 Bài tập giải tam giác vuông . Bài tập 35 SGK trang 94 Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là 19 : 28 , tìm các góc của nó . Tỉ số giữa hai cạnh góc vuông của một tam giác vuông tỉ số lượng giác nào của góc nhọn trong tam giác vuông đó ? Giả sử tỉ số đó là tg của góc nhọn của tam giác vuông . ta có gì ? Suy ra ? Độ lớn góc nhọn kia ? Bài tập 36 SGK trang 94 Cho tam giác có một góc bằng 450 . Đường cao chia một cạnh kề góc đó thành các phần 20 cm và 21 cm . Tính cạnh lớn trong hai cạnh còn lại . Giả sử tam giác ABC có = 450 , đường cao AH mà BH = 20 , HC = 21 Thì cạnh lớn trong hai cạnh còn lại là gì ? Tìm AC dựa trên công thức nào ? Độ dài nào cần tìm ? Vì sao ? Nêu trường hợp BH = 21 và HC = 20 Trả lời và viết cụng thức . Giải và trỡnh bày cỏc bàu tập . LÍ THUYẾT . CÁC KIẾN THỨC CẦN NHỚ . b , c H a c, A C b 1) 2) 3) ah = bc 4) 2/ a) sin = , cos = tg = , cotg = b) sin = cos , cos = sin tg = cotg , cotg = tg 3/ a)b = a. sin = a. cos c = a. sin = a. cos b)b = c. tg = c. cotg c = b. tg = b. cotg 4/Để giải một tam giác vuông cần biết một góc và một cạnh hoặc hai cạnh . Như Vậy Để giải một tam giác vuông cần biết ít nhất một cạnh Bài tập 33 , 34 SGK trang 93 , 94 Đáp án : 33a) C ; b) D ; c) C 34a) C ; b ) C Bài tập 35 SGK trang 94 Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn hoặc cotg của góc kia . Giả sử tỉ số đó là tg của góc nhọn của tam giác vuông . ta có : tg = 19 : 28 0,6786 Suy ra : 340 10/ Số đo góc nhọn kia là : 900 -340 10/ 550 50/ Bài tập 36 SGK trang 94 Giải : Trường hợp BH = 20 , HC = 21 Tam giác AHB vuông tại H , có = 450 Nên Vuông cân tại H . Ta có : AH = HB = 20 Tam giác AHC vuông tại H , ta có : AC = = = 29 c m Trường hợp BH = 21 , HC = 20 Thì AB là cạnh lớn nhất Ta có AB = 21 IV. Luyện tập - Củng cố : V . Hướng dẫn về nhà : Học thuộc lớ thuyết và cỏc cụng thức . Xem cỏc BT đó giải . Giải cỏc bài tập cũn lại . VI. Rỳt kinh nghiệm : TIẾT 18 : ễN TẬP CHƯƠNG I ( TT ) Ngày soạn Ngày dạy I . Mục tiờu : + Hệ thống hoỏ cỏc hệ thức về cạnh và gúc trong tam giỏc vuụng . Rốn luyện kĩ năng dựng gúc khi biết một tỉ số lượng giỏc của nú , kĩ năng giải tam giỏc vuụng và vận dụng vào trong thực tế , giải cỏc BT cú liờn quan đến hệ thức lượng trong tam giỏc vuụng . II. Chuẩn bị : Thước . Compa . Bảng phụ . Cỏc BT . III. Tiến trỡnh bài dạy : 1/Bài cũ : 2/Nội dung : TG Hoạt động của GV Hoạt động của HS Nội dung Đưa ra BT 35SBT Hướng dẫn HS cỏch dựng . Y/c HS dựng và trỡnh bày . Nờu cỏch dựng Nhận xột . Sửa . Bài tập 37SGK trang 94 Cho tam giác ABC có AB = 6 c m , AC = 4,5 c m , BC = 7,5 c m . Chứng minh tam giác ABC vuông tại A . Tính các góc B , C và đường cao của tam giác đó . b)Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào ? Đã biết 3 cạnh , dùng định lí nào để khẳng định tam giác ABC vuông tại A Tìm góc bằng gì ? Công thức tính đường cao trong tam giác vuông . Tam giác MBC có gì giống nhau ? Để diện tích bằng nhau thì cần diều kiện gì ? Vậy M nằm trên đường nào ? Bài tập 42 : ở một cái thang dài 3 m người ta ghi : “ Để đảm bảo an toàn , phải đặt thang này tạo với mặt đất một góc có độ lớn từ 600 đến 700 . Đo góc khó hơn đo độ dài . Vậy hãy cho biết : Khi dùng thang đó chân thang phải đặt cách tường khoảng bao nhiêu m để đảm bảo an toàn ” Hướng dẫn : ở vị trí C thang tạo với mặt đất 700 , ở vị trí D thang tạo với mặt đất một góc 600 . Vậy chân thang phải nằm ở khoảng nào ? Khoảng cách từ đó đến chân tường ra sao ? Tìm gì ? Nêu bài 43 ( nếu còn thời gian Dựng hỡnh Định lí Pitago đảo tỉ số lượng giác của góc đó . ah = bc Cùng cạnh BC Đường cao ứng với cạnh đó bằng nhau . M nằm trên hai đường thẳng song song với BC và cách BC một khoảng cách bằng AH . Khoảng DC Lớn hơn CB và nhỏ hơn DB CB và DB Bài tập 35 SBT/94 Dựng gúc nhọn biết sin = 0,25 cos = 0,75 tg = 1 cotg = 2 Bài tập 37 : a)Ta có : 62 + 4,52 = 7,52 Suy ra : AB2 + AC2 = BC2 Nên tam giác ABC vuông tại A Có tg B = 4,5 : 6 = 0,75 370 và 900 –370 530 AH là đường cao Nên : AB.AC = AH. BC AH = = 3,6 Gọi MK là đường cao của tam giác MBC ta có : SMBC = BC.MK Mà : SABC = BC.AH Để SMBC = SABC thì MK = AH = 3,6 c m Vậy M nằm trên hai đường thẳng song song với BC và cách BC một khoảng cách bằng 3,6 c m . Bài tập 42 trang 96 Giả sử thang được đặt như hình vẽ . Ta có : CB = AC . cos C = 3.cos 700 3.0,3420 1,03 m Và DB = DE . cos D = 3 . cos 600 = 3.0,5 = 1,5 m Vậy khi dùng thang này phải đặt chân thang cách chân tường một khoảng từ 1,03 m đến 1,5 m để đảm bảo an toàn . IV. Luyện tập - Củng cố : V . Hướng dẫn về nhà : ễn tập lớ thuyết và cỏc BT của chương để tiết sau kiểm tra một tiết . BTVN : 41 SGK / 96 . BT 87 , 88 , 89 , 90 SBT / 103 , 104 VI. Rỳt kinh nghiệm : Họ và tờn : ............................................................. KIỂM TRA 1 TIẾT Lớp : 9/3 MễN : HèNH HỌC 9 – Bài số 1. PHẦN TRẮC NGHIỆM : Chọn cõu trả lời đỳng : Cõu 1 :( 2đ ) Cho tam giỏc ABC vuụng tại A , AB = 3cm ; AC = 4cm ; AH là đường cao . Lỳc đú : 1.Độ dài của BC bằng : a. 5 cm b. 6 cm c. 7 cm d. 8 cm 2.Độ dài của BH bằng : a. cm b. cm c. cm d . 3 cm 3. Độ dài của CH bằng : a. cm b. cm c. cm d. 5 cm 4. Độ dài AH bằng : a. cm b. cm c. cm d. cm Cõu 2 :( 2đ ) Cho gúc nhọn . Hóy lựa chọn giỏ trị thớch hợp điền vào dấu chấm . 1.sin ( 900 - ) = ............................ a. sin b. cos c. tg d. cotg 2. cos ( 900 - ) = ............................ a. sin b. cos c. tg d. cotg 3. tg ( 900 - ) = ............................ a. sin b. cos c. tg d. cotg 4. cotg ( 900 - ) = ............................ a. sin b. cos c. tg d. cotg Cõu 3 : ( 1đ ) Giỏ trị của biểu thức bằng : a. 1 b. 2 c. 3 d . 4 Cõu 4 : PHẦN TỰ LUẬN : Cõu 1 :( 2 đ ) Cho tam giỏc ABC vuụng tại A , đường cao AH . Biết BH = 4 cm ; AB = 6 cm .Hóy giải tam giỏc ABC Cõu 2 :( 3đ ) Cho tam giỏc ABC vuụng tại A , AB = 3 cm , AC = 4 cm . Tớnh BC , B , C . Phõn giỏc của gúc A cắt BC tại E . Tớnh BE , CE . Từ E kẻ EM và EN lần lượt vuụng gúc với AB và AC . Chứng minh tứ giỏc AMEN là hỡnh vuụng . Tớnh chu vi và diện tớch của tứ giỏc AMEN
Tài liệu đính kèm:
 GA HH9 C1 3cot.doc
GA HH9 C1 3cot.doc





