Giáo án Hình học Khối 8 - Chương trình cơ bản - Năm học 2011-2012
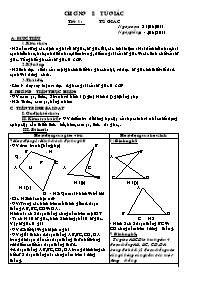
* Hoạt động 2: Định nghĩa tứ giác lồi
-GV: Hãy lấy mép thước kẻ lần lượt đặt trùng lên mỗi cạch của tứ giác ở H1 rồi quan sát
- H1(a) luôn có hiện tượng gì xảy ra ?
- H1(b) (c) có hiện tượng gì xảy ra ?
- GV: Bất cứ đương thẳng nào chứa 1 cạnh của hình H1(a) cũng không phân chia tứ giác thành 2 phần nằm ở 2 nửa mặt phẳng có bờ là đường thẳng đó gọi là tứ giác lồi.
- Vậy tứ giác lồi là tứ giác như thế nào ?
+ Trường hợp H1(b) & H1 (c) không phải là tứ giác lồi
* Hoạt động 3: Nêu các khái niệm cạnh kề đối, góc kề, đối điểm trong , ngoài.
GV: Vẽ H3 và giải thích khái niệm:
GV: Không cần tính số mỗi góc hãy tính tổng 4 góc
+ + + = ? (độ)
- Gv: ( gợi ý hỏi)
+ Tổng 3 góc của 1 là bao nhiêu độ?
+ Muốn tính tổng + + + = ? (độ) ( mà không cần đo từng góc ) ta làm ntn?
+ Gv chốt lại cách làm:
- Chia tứ giác thành 2 có cạnh là đường chéo
- Tổng 4 góc tứ giác = tổng các góc của 2 ABC & ADC Tổng các góc của tứ giác bằng 3600
- GV: Vẽ hình & ghi bảng
Chương I: Tứ giác Tiết 1: Tứ giác Ngày soạn: 21/08/2011 Ngày giảng: ./08/2011 A- mục tiêu 1. Kiến thức: - HS nắm vững các định nghĩa về tứ giác, tứ giác lồi, các khái niệm : Hai đỉnh kề nhau, hai cạnh kề nhau, hai cạnh đối nhau, điểm trong, điểm ngoài của tứ giác & các tính chất của tứ giác. Tổng bốn góc của tứ giác là 3600. 2. Kỹ năng: - HS tính được số đo của một góc khi biết ba góc còn lại, vẽ được tứ giác khi biết số đo 4 cạnh & 1 đường chéo. 3. Thái độ: - Rèn tư duy suy luận ra được 4 góc ngoài của tứ giác là 3600 B-phương tiện thực hiện: - GV: com pa, thước, 2 tranh vẽ hình 1 ( sgk ) Hình 5 (sgk) bảng phụ - HS: Thước, com pa, bảng nhóm C- Tiến trình bài dạy I. Ôn định tổ chức: II. Kiểm tra bài cũ:- GV: kiểm tra đồ dùng học tập của học sinh và nhắc nhở dụng cụ học tập cần thiết: thước kẻ, ê ke, com pa, thước đo góc, III. Bài mới : Hoạt động của giáo viên Hoạt động của học sinh * Hoạt động 1: Hình thành định nghĩa - GV: treo tranh (bảng phụ) B B . N Q . P C A M A C D H1(b) H1 (a) D - HS: Quan sát hình & trả lời - Các HS khác nhận xét -GV: Trong các hình trên mỗi hình gồm 4 đoạn thẳng: AB, BC, CD & DA. Hình nào có 2 đoạn thẳng cùng nằm trên một ĐT - Ta có H1 là tứ giác, hình 2 không phải là tứ giác. Vậy tứ giác là gì ? - GV: Chốt lại & ghi định nghĩa - GV: giải thích : 4 đoạn thẳng AB, BC, CD, DA trong đó đoạn đầu của đoạn thẳng thứ nhất trùng với điểm cuối của đoạn thẳng thứ 4. + 4 đoạn thẳng AB, BC, CD, DA trong đó không có bất cứ 2 đoạn thẳng nào cùng nằm trên 1 đường thẳng. + Cách đọc tên tứ giác phải đọc hoặc viết theo thứ tự các đoạn thẳng như: ABCD, BCDA, ADBC +Các điểm A, B, C, D gọi là các đỉnh của tứ giác. + Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh của tứ giác. * Hoạt động 2: Định nghĩa tứ giác lồi -GV: Hãy lấy mép thước kẻ lần lượt đặt trùng lên mỗi cạch của tứ giác ở H1 rồi quan sát - H1(a) luôn có hiện tượng gì xảy ra ? - H1(b) (c) có hiện tượng gì xảy ra ? - GV: Bất cứ đương thẳng nào chứa 1 cạnh của hình H1(a) cũng không phân chia tứ giác thành 2 phần nằm ở 2 nửa mặt phẳng có bờ là đường thẳng đó gọi là tứ giác lồi. - Vậy tứ giác lồi là tứ giác như thế nào ? + Trường hợp H1(b) & H1 (c) không phải là tứ giác lồi * Hoạt động 3: Nêu các khái niệm cạnh kề đối, góc kề, đối điểm trong , ngoài. GV: Vẽ H3 và giải thích khái niệm: GV: Không cần tính số mỗi góc hãy tính tổng 4 góc + + + = ? (độ) - Gv: ( gợi ý hỏi) + Tổng 3 góc của 1 là bao nhiêu độ? + Muốn tính tổng + + + = ? (độ) ( mà không cần đo từng góc ) ta làm ntn? + Gv chốt lại cách làm: - Chia tứ giác thành 2 có cạnh là đường chéo - Tổng 4 góc tứ giác = tổng các góc của 2 ABC & ADC Tổng các góc của tứ giác bằng 3600 - GV: Vẽ hình & ghi bảng 1) Định nghĩa B A C D H1(c) A B ‘ D C H2 - Hình 2 có 2 đoạn thẳng BC & CD cùng nằm trên 1 đường thẳng. * Định nghĩa: Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kỳ 2 đoạn thẳng nào cũng không cùng nằm trên một đường thẳng. * Tên tứ giác phải được đọc hoặc viết theo thứ tự của các đỉnh. *Định nghĩa tứ giác lồi * Định nghĩa: (sgk) * Chú ý: Khi nói đến 1 tứ giác mà không giải thích gì thêm ta hiểu đó là tứ giác lồi + Hai đỉnh thuộc cùng một cạnh gọi là hai đỉnh kề nhau + hai đỉnh không kề nhau gọi là hai đỉnh đối nhau + Hai cạnh cùng xuất phát từ một đỉnh gọi là hai cạnh kề nhau + Hai cạnh không kề nhau gọi là hai cạnh đối nhau - Điểm nằm trong M, P điểm nằm ngoài N, Q 2/ Tổng các góc của một tứ giác ( HD4) B 1 A 1 2 C 2 D Â1 + + 1 = 1800 2 + + 2 = 1800 (1+2)++(1+2) + = 3600 Hay + + + = 3600 * Định lý: SGK IV. Củng cố - GV: cho HS làm bài tập trang 66. Hãy tính các góc còn lại V. Hướng dẫn HS học tập ở nhà - Nêu sự khác nhau giữa tứ giác lồi & tứ giác không phải là tứ giác lồi ? - Làm các bài tập : 2, 3, 4 (sgk) * Chú ý : T/c các đường phân giác của tam giác cân * HD bài 4: Dùng com pa & thước thẳng chia khoảng cách vẽ tam giác có 1 cạnh là đường chéo trước rồi vẽ 2 cạch còn lại * Bài tập cho hs giỏi Cho tứ giác lồi ABCD chứng minh rằng: đoạn thẳng MN nối trung điểm của 2 cạnh đối diện nhỏ hơn hoặc bằng nửa tổng 2 cạnh còn lại (Gợi ý: Nối trung điểm đường chéo). Tiết 2 Hình thang Ngày soạn: 21/08/2011 Ngày giảng: /08/2011 A- mục tiêu 1. Kiến thức: - HS nắm vững các định nghĩa về hình thang , hình thang vuông các khái niệm : cạnh bên, đáy , đường cao của hình thang 2. Kỹ năng: - Nhận biết hình thang hình thang vuông, tính được các góc còn lại của hình thang khi biết một số yếu tố về góc. 3. Thái độ: - Rèn tư duy suy luận, sáng tạo B- phương tiện thực hiện: - GV: com pa, thước, tranh vẽ bảng phụ, thước đo góc - HS: Thước, com pa, bảng nhóm C- Tiến trình bài dạy I. Ôn định tổ chức: II. Kiểm tra bài cũ:- GV: (dùng bảng phụ ) * HS1: Thế nào là tứ giác lồi ? Phát biểu ĐL về tổng 4 góc của 1 tứ giác ? * HS 2: Góc ngoài của tứ giác là góc như thế nào ?Tính các góc ngoài của tứ giác A B 1 1 1 B 900 C 1 750 1200 1 C A 1 D D 1 III. Bài mới: Hoạt động của giáo viên Hoạt động của học sinh * Hoạt động 1: ( Giới thiệu hình thang) - GV: Tứ giác có tính chất chung là + Tổng 4 góc trong là 3600 + Tổng 4 góc ngoài là 3600 Ta sẽ nghiên cứu sâu hơn về tứ giác. - GV: đưa ra hình ảnh cái thang & hỏi + Hình trên mô tả cái gì ? + Mỗi bậc của thang là một tứ giác, các tứ giác đó có đặc điểm gì ? & giống nhau ở điểm nào ? - GV: Chốt lại + Các tứ giác đó đều có 2 cạnh đối // Ta gọi đó là hình thang ta sẽ nghiên cứu trong bài hôm nay. * Hoạt động 2: Định nghĩa hình thang - GV: Em hãy nêu định nghĩa thế nào là hình thang - GV: Tứ giác ở hình 13 có phải là hình thang không ? vì sao ? - GV: nêu cách vẽ hình thang ABCD + B1: Vẽ AB // CD + B2: Vẽ cạnh AD & BC & đương cao AH - GV: giới thiệu cạnh. đáy, đường cao * Hoạt động 3: Bài tập áp dụng - GV: dùng bảng phụ hoặc đèn chiếu B C 600 600 A D (H. a) E I N F 1200 G 1050 M 1150 750 H K 1 (H.b) (H.c) - Qua đó em hình thang có tính chất gì ? * Hoạt động 4: ( Bài tập áp dụng) GV: đưa ra bài tập HS làm việc theo nhóm nhỏ Cho hình thang ABCD có 2 đáy AB & CD biết: AD // BC. CMR: AD = BC; AB = CD A B ABCD là hình thang GT đáy AB & CD AD// BC KL AB=CD: AD= BC D C Bài toán 2: A B ABCD là hình thang GT đáy AB & CD AB = CD KL AD// BC; AD = BC D C - GV: qua bài 1 & bài 2 em có nhận xét gì ? * Hoạt động 5: Hình thang vuông 1) Định nghĩa Hình thang là tứ giác có hai cạnh đối song song A B D H C * Hình thang ABCD : + Hai cạnh đối // là 2 đáy + AB đáy nhỏ; CD đáy lớn + Hai cạnh bên AD & BC + Đường cao AH (H.a)= = 600 AD// BC Hình thang - (H.b)Tứ giác EFGH có: = 750 = 1050 (Kề bù) = = 1050 GF// EH Hình thang - (H.c) Tứ giác IMKN có: = 1200 = 1200 IN không song song với MK đó không phải là hình thang * Nhận xét: + Trong hình thang 2 góc kề một cạnh bù nhau (có tổng = 1800) + Trong tứ giác nếu 2 góc kề một cạnh nào đó bù nhau Hình thang. * Bài toán 1 - Hình thang ABCD có 2 đáy AB & CD theo (gt)AB // CD (đn)(1) mà AD // BC (gt) (2) Từ (1) & (2)AD = BC; AB = CD ( 2 cắp đoạn thẳng // chắn bởi đương thẳng //.) * Bài toán 2: (cách 2) ABC = ADC (g.c.g) * Nhận xét 2: (sgk)/70. 2) Hình thang vuông Là hình thang có một góc vuông. A B D C IV.Củng cố :- GV: đưa bài tập 7 ( Bằng bảng phụ) . Tìm x, y ở hình 21 V. Hướng dẫn HS học tập ở nhà: - Học bài. Làm các bài tập 6,8,9 - Trả lời các câu hỏi sau:+ Khi nào một tứ giác được gọi là hình thang. + Khi nào một tứ giác được gọi là hình thang vuông. Tiết 3: Hình thang cân Ngày soạn: 26/08/2011 Ngày giảng: ./08/2011 I- mục tiêu 1. Kiến thức: - HS nắm vững các đ/n, các t/c của hình thang cân 2. Kỹ năng: - Nhận biết hình thang hình thang cân, biết vẽ hình thang cân, biết sử dụng định nghĩa, các tính chất vào chứng minh, biết chứng minh 1 tứ giác là hình thang cân 3. Thái độ: A D C B x y 1200 600 - Rèn tư duy suy luận, sáng tạo II-phương tiện thực hiện: - GV: com pa, thước, tranh vẽ bảng phụ, thước đo góc - HS: Thước, com pa, bảng nhóm Iii- Tiến trình bài dạy A- Ôn định tổ chức: B- Kiểm tra bài cũ:- HS1: GV dùng bảng phụ Cho biết ABCD là hình thang có đáy là AB, & CD. Tính x, y của các góc D, B - HS2: Phát biểu định nghĩa hình thang & nêu rõ các khái niệm cạnh đáy, cạnh bên, đường cao của hình thang - HS3: Muốn chứng minh một tứ giác là hình thang ta phải chứng minh như thế nào? C- Bài mới: Hoạt động của giáo viên Hoạt động của học sinh Hoạt động 1: Định nghĩa Yêu cầu HS làm ? Nêu định nghĩa hình thang cân. GV: dùng bảng phụ a) Tìm các hình thang cân ? b) Tính các góc còn lại của mỗi HTC đó c) Có NX gì về 2 góc đối của HTC? A B E F 800 800 1000 D C 800 800 (a) G (b) H ( Hình (b) không phải vì + 1800 * Nhận xét: Trong hình thang cân 2 góc đối bù nhau. * Hoạt động 2:Hình thành T/c, Định lý 1 Trong hình thang cân 2 góc đối bù nhau. Còn 2 cạnh bên liệu có bằng nhau không ? - GV: cho các nhóm CM & gợi ý AD không // BC ta kéo dài như thế nào ? - Hãy giải thích vì sao AD = BC ? ABCD là hình thang cân GT ( AB // DC) KL AD = BC O Các nhóm CM: A 2 2 B 1 1 D C + AD // BC ? khi đó hình thang ABCD có dạng như thế nào ? * Hoạt động 3: Giới thiệu địmh lí 2 - GV: Với hình vẽ sau 2 đoạn thẳng nào bằng nhau ? Vì sao ? - GV: Em có dự đoán gì về 2 đường chéo AC & BD ? GT ABCD là hình thang cân ( AB // CD) KL AC = BD GV: Muốn chứng minh AC = BD ta phải chứng minh 2 tam giác nào bằng nhau ? 1) Định nghĩa Hình thang cân là hình thang có 2 góc kề một đáy bằng nhau Tứ giác ABCD Tứ giác ABCD là H. thang cân AB // CD ( Đáy AB; CD) = hoặc = I 700 N P Q K 1100 700 T S (c) M (d) a) Hình a,c,d là hình thang cân b) Hình (a): = 1000 Hình (c) : = 700 Hình (d) : = 900 c)Tổng 2 góc đối của HTC là 1800 2) Tính chất * Định lí 1: Trong hình thang cân 2 cạnh bên bằng nhau. Chứng minh: AD cắt BC ở O ( Giả sử AB < DC) ABCD là hình thang cân nên = ta có= nên ODC cân ( 2 góc ở đáy bằng nhau) OD = OC (1) = nên = OAB cân (2 góc ở đáy bằng nhau) OA = OB (2) Từ (1) &(2) OD - OA = OC - OB Vậy AD = BC b) AD // BC khi đó AD = BC * Chú ý: SGK * Định lí 2: Trong hình thang cân 2 đường chéo bằng nhau. Chứng minh: ADC & BCD có: + CD cạnh chung + = ( Đ/ N hình thang cân ) + AD = BC ( cạnh của hình thang cân) ADC = BCD ( c.g.c) AC = BD D) Củng cố: GV: Dùng bảng phụ HS trả lời a) Trong hình vẽ có những cặp đoạn thẳng nào bằng nhau ? Vì sao ? b) Có những góc nào bằng nhau ? Vì sao ? c) Có những tam giác nào bằng nhau ? Vì sao ? E) Hướng dẫn HS học tập ở nhà:- Học bài.Xem lại chứng minh các định lí - ... 64 hình chóp đều và hình chóp cụt đều Ngày soạn: 4/4/2012 Ngày giảng: 7/5/2012 A- Mục tiêu bài dạy: 1. Kiến thức: -Từ mô hình trực quan, GV giúp h/s nắm chắc các yếu tố của hình chóp và hình chóp cụt đều. Nắm được cách gọi tên theo đa giác đáy của nó. Nắm được các yếu tố đáy, mặt bên, chiều cao 2. Kỹ năng: - Rèn luyện kỹ năng vẽ hình hình chóp và hình chóp cụt đều theo 3 bước: Đáy, mặt bên, đáy thứ 2 3. Thái độ: - Giáo dục cho h/s tính thực tế của các khái niệm toán học. B- phương tiện thực hiện: - GV: Mô hình hình hình chóp và hình chóp cụt đều. Bảng phụ ( tranh vẽ ) - HS: Bìa cứng kéo băng keo C- tiến trình bài dạy: I- Tổ chức: 8A 8B II- Kiểm tra bài cũ: Lồng vào bài mới III- Bài mới: Hoạt động của GV Hoạt động của HS * HĐ1: Giới thiệu hình chóp - GV: Dùng mô hình giới thiệu cho HS khái niệm hình chóp, dùng hình vẽ giới thiệu các yếu tố có liên quan, từ đó hướng dẫn cách vẽ hình chóp - GV: Đưa ra mô hình chóp cho HS nhận xét: - Đáy của hình chóp ? - Các mặt bên là các tam giác - Đường cao SH * HĐ2: Hình thành khái niệm hình chóp đều - GV: Đưa ra mô hình chóp đều cho HS nhận xét: - Đáy của hình chóp - Các mặt bên là các tam giác - Đường cao SH Khái niệm : SGK/ 117 S. ABCD là hình chóp đều : ( ABCD) là đa giác đều SBC = SBA = SDC = ? . Cắt tấm bìa hình 118 rồi gấp lại thành hình chóp đều. GV yêu cầu HS làm bài tập 37/ SGK tr118 * HĐ3: Hình thành khái niệm hình chóp cụt đều - GV: Cho HS quan sát và cắt hình chóp thành hình chóp cụt - Nhận xét mặt phẳng cắt - Nhận xét các mặt bên 1) Hình chóp - Đáy là một đa giác - Các mặt bên là các tam giác có chung 1 đỉnh S A B C D H - SAB, SBC, SCD, SDA là các mặt bên - SH (ABCD) là đường cao - S là đỉnh - Mặt đáy: ABCD Hình chóp S.ABCD có đỉnh là S, đáy là tứ giác ABCD, ta gọi là hình chóp tứ giác S B H Hình chóp đều D C A - Đáy là một đa giác đều - Các mặt bên là các tam giác cân = nhau - Đường cao trùng với tâm của đáy - Hình chóp tứ giác đều có mặt đáy là hình vuông, các mặt bên là các tam giác cân - Chân đường cao H là tâm của đường tròn đi qua các đỉnh của mặt đáy - Đường cao vẽ từ đỉnh S của mỗi mặt bên của hình chóp đều gọi là trung đoạn của hình chóp đó Trung đoạn của hình chóp không vuông góc với mặt phẳng đáy, chỉ vuông góc cạnh đáy của hình chóp ? Cắt tấm bìa hình 118 rồi gấp lại thành hình chóp đều. Bài tập 37/ SGK tr118 a.Sai, vì hình thoi không phảI là tứ giác đều b.Sai, vì hình chữ nhật không phải là tứ giác đều 3) Hình chóp cụt đều A C S B D H + Cắt hình chóp bằng một mặt phẳng // đáy của hình chóp ta được hình chóp cụt - Hai đáy của hình chóp cụt đều // Nhận xét :- Các mặt bên của hình chóp cụt là các hình thang cân IV: Củng cố - HS đứng tại chỗ trả lời bài 37 - HS làm bài tập 38 Điền vào bảng - Hình chóp cụt đều có hai mặt đáy là 2 đa giác đều đồng dạng với nhau Chóp tam giác đều Chóp tứ giác đều Chóp ngũ giác đều Chóp lục giác đều Đáy Tam giác đều Hình vuông Ngũ giác đều Lục giác đều Mặt bên Tam giác cân Tam giác cân Tam giác cân Tam giác cân------ Số cạnh đáy 3 4 5 6 Số cạnh 6 8 10 12 Số mặt 4 5 6 7 V: Hướng dẫn về nhà - Làm các bài tập 38, 39 sgk/119 c Tiết 65 Diện tích xung quanh hình chóp đều Ngày soạn: 4/4/2012 Ngày giảng: 9/5/2012 A- Mục tiêu bài dạy: 1. Kiến thức: -Từ mô hình trực quan, GV giúp HS nắm chắc công thức tính S xung quanh của hình chóp đều.Nắm được cách gọi tên theo đa giác đáy của nó. Nắm được các yếu tố đáy, mặt bên, chiều cao. 2. Kỹ năng: - Rèn luyện kỹ năng tính diện tích xung quanh hình chóp. 3. Thái độ: - Giáo dục cho h/s tính thực tế của các khái niệm toán học. B- phương tiện thực hiện: - GV: Mô hình hình hình chóp đều, và hình lăng trụ đứng. Bảng phụ - HS: Bìa cứng kéo băng keo C- tiến trình bài dạy: I- Tổ chức: 8A 8B II- Kiểm tra bài cũ: - Phần làm bài tập ở nhà của HS III- Bài mới: Hoạt động của GV Hoạt động của HS * HĐ1: Giới thiệu công thức tính diện tích xung quanh hình chóp GV: Yêu cầu HS đưa ra sản phẩm bài tập đã làm ở nhà & kiểm tra bằng câu hỏi sau: - Có thể tính được tổng diện tích của các tam giác khi chưa gấp? - Nhận xét tổng diện tích của các tam giác khi gấp và diện tích xung quanh hình hình chóp đều? a.Số các mặt bằng nhau trong 1 hình chóp tứ giác đều là: b.Diện tích mỗi mặt tam giác là: c.Diện tích đáy của hình chóp đều.. d.Tổng diện tích các mặt bên của hình chóp đều là: GV giải thích : tổng diện tích tất cả các mặt bên là diện tích xung quanh của hình chóp GV đưa mô hình khai triển hình chóp tứ giác Tính diện tích xung quanh của hình chóp tứ giác đều: GV : Với hình chóp đều nói chung ta có: Tính diện tích toàn phần của hình chóp đều thế nào? áp dụng: Bài 43 a/ SGK/ 121 - GV: Cho HS thảo luận nhóm bài tập VD *HĐ2: Ví dụ Hình chóp S.ABCD 4 mặt là tam giác đều bằng nhau H là tâm đường tròn ngoại tiếp tam giác đều ABC bán kính HC = R = Biết AB = R S A C I H B 1) Công thức tính diện tích xung quanh - Tính được S của các tam giác đó bằng công thức - Sxq = tổng diện tích các mặt bên ?a. Là 4 mặt, mỗi mặt là 1 tam giác cân = 12 cm2 4. 4 = 16 cm2 12 . 4 = 48 cm2 Diện tích xung quanh của hình chóp tứ giác đều: Diện tích mỗi tam giác là: Sxq của tứ giác đều: S Xq = p. d Sxq = 4. = = P. d Công thức: SGK/ 120 p: Nửa chu vi đáy d: Trung đoạn hình chóp đều * Diện tích toàn phần của hình chóp đều: Stp = Sxq + Sđáy Bài 43 a/ SGK: S Xq = p. d = = 800 cm2 Stp = Sxq + Sđáy= 800 + 20 . 20 = 1200 cm2 2) Ví dụ: Hình chóp S.ABCD đều nên bán kính đường tròn ngoại tiếp tam giác đều là R Nên AB = R = = 3 ( cm) * Diện tích xung quanh hình hình chóp : S xq = p.d = ( cm2) A C S B D H IV: Củng cố Chữa bài tập 40/121 * Chữa bài tập 40/121 + Trung đoạn của hình chóp đều: SM2 = 252 - 152 = 400 SM = 20 cm + Nửa chu vi đáy: 30. 4 : 2 = 60 cm + Diện tích xung quanh hình hình chóp đều: 60 . 20 = 1200 cm2 + Diện tích toàn phần hình chóp đều: 1200 + 30.30 = 2100 cm2 V: Hướng dẫn về nhà - Làm các bài tập: 41, 42, 43 sgk c Tiết 66 Thể tích của hình chóp đều Ngày soạn: 4/4/2012 Ngày dạy 8A 10/5/2012 8B 11/5/2012 A- Mục tiêu bài dạy: -Từ mô hình trực quan, GV giúp HS nắm chắc công thức tính Vcủa hình chóp đều. - Rèn luyện kỹ năng tính thể tích hình chóp . Kỹ năng quan sát nhận biết các yếu tố của hình chóp đều qua nhiều góc nhìn khác nhau. Kỹ năng vẽ hình chóp. - Giáo dục cho HS tính thực tế của các khái niệm toán học. B- phương tiện thực hiện: - GV: Mô hình hình hình chóp đều, và hình lăng trụ đứng. Dụng cụ đo lường - HS: Công thức tính thể tích hình lăng trụ đứng C- tiến trình bài dạy: I- Tổ chức: 8A 8B II- Kiểm tra bài cũ: - Phát biểu công thức tính thể tích hình lăng trụ đứng. áp dụng tính chiều cao của hình lăng trụ đứng tứ giác đều có dung tích là 3600 lít và cạnh hình vuông của đáy là 3 m III- Bài mới: Hoạt động của GV Hoạt động của HS * HĐ1: Giới thiệu công thức tính thể tích của hình chóp đều - GV: đưa ra hình vẽ lăng trụ đứng tứ giác và nêu mối quan hệ của thể tích hai hình lăng trụ đứng có đáy là đa giác đều và một hình chóp đều có chung đáy và cùng chiều cao - GV: Cho HS làm thực nghiệm để chứng minh thể tích của hai hình trên có mối quan hệ biểu diễn dưới dạng công thức Vchóp đều = S. h + S: là diện tích đáy + h: là chiều cao * Chú ý: Người ta có thể nói thể tích của khối lăng trụ, khối chóp thay cho khối lăng trụ, khối chóp * HĐ2: Các ví dụ * Ví dụ 1: sgk * Ví dụ 2: Tính thể tích của hình chóp tam giác đều chiều cao hình chóp bằng 6 cm, bán kính đường tròn ngoại tiếp là 6 cm * HĐ3: Tổ chức luyện tập * Vẽ hình chóp đều - Vẽ đáy, xác định tâm (0) ngoại tiếp đáy - Vẽ đường cao của hình chóp đều - Vẽ các cạnh bên ( Chú ý nét khuất) 1) Thể tích của hình chóp đều A' S D' B' A B C D C' HS vẽ và làm thực nghiệm rút ra CT tính V hình chóp đều Vchóp đều = S. h - HS làm ví dụ + Đường cao của tam giác đều: ( 6: 2). 3 = 9 cm Cạnh của tam giác đều: a2 - = h a = 2. h . = 10,38 cm IV: Củng cố chữa bài 44/123 a) HS chữa b) Làm bài tập sau + Đường cao của hình chóp = 12 cm; AB = 10 cm Tính thể tích của hình chóp đều? + Cho thể tích của hình chóp đều 18 cm3 Cạnh AB = 4 cm Tính chiều cao hình chóp? S B D H C A - HS làm việc theo nhóm * Đường cao của tam giác AB * Diện tích đáy: * Thể tích của hình chóp đều V = *Ta có: V: Hướng dẫn về nhà - Làm các bài tập 45, 46/sgk - Xem trước bài tập luyện tập Tiết 67 ôn tập chương iv Ngày soạn: 4/4/2012 Ngày dạy 8A 10/5/2012 8B ..../.../2012 A- Mục tiêu bài dạy: - GV giúp HS nắm chắc kiến thức có liên quan đến hình chóp đều - công thức tính thể tích của hình chóp đều. - Rèn luyện kỹ năng tính thể tích hình chóp . Kỹ năng quan sát nhận biết các yếu tố của hình chóp đều qua nhều góc nhìn khác nhau. Kỹ năng vẽ hình chóp. - Giáo dục cho HS tính thực tế của các khái niệm toán học. B- phương tiện thực hiện: - GV: Mô hình hình hình chóp đều, và hình lăng trụ đứng. Bài tập - HS: công thức tính thể tích các hình đã học - Bài tập C- tiến trình bài dạy: I- Tổ chức: 8A 8B II- Kiểm tra: III- Bài mới HĐ 1. Hệ thống hóa kiến thức cơ bản Hình Sxung quanh Stoàn phần Thể tích C1 B1 C D1 A1 D A * Lăng trụ đứng - Các mặt bên là B hình chữ nhật - Đáy là đa giác * Lăng trụ đều: Lăng trụ đứng đáy là đa giác đều Sxq = 2 p .h P: Nửa chu vi đáy h: chiều cao Stp= Sxq + 2 Sđáy V = S. h S: diện tích đáy h: chiều cao B C F G A D E H * Hình hộp chữ nhật: Hình có 6 mặt là hình chữ nhật Sxq= 2(a+b)c a, b: 2 cạnh đáy c: chiều cao Stp=2(ab+ac+bc) V = abc A' S D' B' A B C D C' S B D H * Hình lập phương: Hình hộp chữ nhật có 3 kích thước bằng nhau. Các mặt bên đều là hình vuông Sxq= 4 a2 a: cạnh hình lập phương Stp= 6 a2 V = a3 Chóp đều: Mặt đáy L à đa giác đều C A Sxq = p .d P: Nửa chu vi đáy d: chiều cao mặt bên ( trung đoạn) Stp= Sxq + Sđáy V = S. h S: diện tích đáy h: chiều cao *HĐ2: Luyện tập 2) Chữa bài 48 - GV: dùng bảng phụ và HS lên bảng tính a) Sxq = p.d = 2.5.4,33 = 43,3 Stp = Saq + S đáy = 43,3 + 25 = 68,3 cm2 3) Chữa bài 49 a) Nửa chu vi đáy: 6.4 : 2 = 12(cm) Diện tích xung quanh là: 12. 10 = 120 (cm2) b) Nửa chu vi đáy: 7,5 . 2 = 15 Diện tích xung quanh là: Sxq = 15. 9,5 = 142,5 ( cm 2) 4) Bài tập 65(1)SBT : Hình vẽ đưa lên bảng phụ B H -HS lên bảng làm BT S D C A BT65: a)Từ tam giác vuông SHK tính SK SK = (m) Tam giác SKB có: SB = (m) b) Sxq= pd 87 235,5 (m2) c) V = S.h2 651 112,8(m3 ) IV: Củng cố - GV: nhắc lại phương pháp tính Sxq ; Stp và V của hình chóp HS nhắc lại các công thức tính đã học. V: Hướng dẫn về nhà - Làm bài 50,52,57
Tài liệu đính kèm:
 giao an hinh 8(3).doc
giao an hinh 8(3).doc





