Giáo án Hình học 8 - Tiết 67: Ôn tập cuối năm (Bản đẹp)
I . MỤC TIÊU :
Qua tiết học này HS cần đạt được :
- Hệ thống các kiến thức trong chương I và chương II đã học theo một sơ đồ và theo bảng tóm tắt các nội dung chủ yếu.
- Tìm hiểu một số cách chứng minh, suy luận thường gặp .
- Tự trình bày chứng minh một bài toán hình học cụ thể theo những suy luận có lý và lôgíc chặt chẽ.
- Nắm vững các trọng tâm của chương trình để thi HKI có kết quả.
II . CHUẨN BỊ CỦA THẤY VÀ TRÒ:
Thầy : Giáo án, các nội dung trọng tâm theo sơ đồ và theo bảng tóm tắt, các dụng cụ học tập.
Trò : các kiến thức đã học chuẩn bị trước dưới các hình thức tự hiểu và tóm tắt chúng.
III . Các hoạt động của thầy và trò:
A . Hoạt động 1 : Tiến hành ôn tập lý thuyết:
GV : Hãy nêu lần lượt các tính chất, định lý đã học trong chương I?
HS Trả lời.
GV : đưa ra các phần nội dung lý thuyết theo bảng mà người thầy chuẩn bị trước để HS tham khảo.
* CHƯƠNG I :
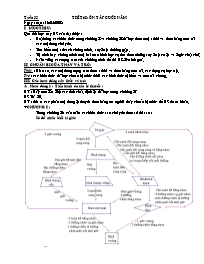
Trong chương I ta cần nắm các kiến thức sau chủ yếu theo sơ đồ sau :
Tuần 35 TIẾT 68: ÔN TẬP CUỐI NĂM Ngày soạn : 13/05/2008 I . MỤC TIÊU : Qua tiết học này HS cần đạt được : Hệ thống các kiến thức trong chương I và chương II đã học theo một sơ đồ và theo bảng tóm tắt các nội dung chủ yếu. Tìm hiểu một số cách chứng minh, suy luận thường gặp . Tự trình bày chứng minh một bài toán hình học cụ thể theo những suy luận có lý và lôgíc chặt chẽ. Nắm vững các trọng tâm của chương trình để thi HKI có kết quả. II . CHUẨN BỊ CỦA THẤY VÀ TRÒ: Thầy : Giáo án, các nội dung trọng tâm theo sơ đồ và theo bảng tóm tắt, các dụng cụ học tập. Trò : các kiến thức đã học chuẩn bị trước dưới các hình thức tự hiểu và tóm tắt chúng. III . Các hoạt động của thầy và trò: A . Hoạt động 1 : Tiến hành ôn tập lý thuyết: GV : Hãy nêu lần lượt các tính chất, định lý đã học trong chương I? HS Trả lời. GV : đưa ra các phần nội dung lý thuyết theo bảng mà người thầy chuẩn bị trước để HS tham khảo. * CHƯƠNG I : Trong chương I ta cần nắm các kiến thức sau chủ yếu theo sơ đồ sau : Sơ đồ nhận biết tứ giác Chương II : HS cần nắm các kiến thức trọng tâm của chương như các định lý tính chất và các định nghĩa liên quan. * Một số công thức tính diện tích : a . Tam Giác : S = a.h Với a là cạnh đáy , h là đường cao tương ứng . b . Hình Chữ Nhật : S = a.b Trong đó : a , b là hai chiều dài và rộng . c . Hình Vuông : S = a2 Trong đó : a là cạnh . d . Hình Thang : S = (a + b) h Trong đó : a ,b là hai đáy , h là đường cao. e . Hình Bình Hành : S = a.h Trong đó : a là độ dài một cạnh và h là chiều cao tương ứng. f . Công thức tính diện tích tứ giác có hai đường chéo vuông góc nhau : S = (Trong đó d và d’ là hai đường chéo} g . Hình thoi : S = (Trong đó d và d’ là hai đường chéo} Có thể tính theo công thức diện tích hình bình hành : S = a.h Trong đó : a ,b là hai đáy , h là đường cao. II . Bài tập : GV : Hãy làm bài tập sau : Cho hình bình hành MNPQ có MN=2 MQ và . Gọi I; K lần lượt là trung điểm của MN và PQ và A là điểm đối xứng của Q qua M. a/ Tứ giác MIKQ là hình gì ? Vì sao? b/ Chứng minh tam giác AMI là tam giác đều. c/ Chứng minh tứ giác AMPN là hình chữ nhât. d/ Cho AI = 4cm. Tính diện tích của hình chữ nhật AMPN. GT KL MNPQ là hình bình hành MN=2MQ; ; MI=IK;KQ=KP;AM=MQ AI = 4cm a/ a/Tứ giác MIKQ là hình gì ? Vì sao? b/AMI là tam giác đều. c/ AMPN là hình chữ nhât. d/ Tính diện tích của hình chữ nhật AMPN V ? Hãy vẽ hình và ghi GT/ KL của bài? ? Hãy tập suy luận để tìm ra cách giải trong từng câu của bài? HS suy nghĩ và thực hiện lên bảng . GV : nhận xét và điều chỉnh sai sót trong quá trình làm bài tập này. Chốt lại các nội dung cần ôn tập trong hình học là lý thuyết chương I và chương II đồng thời cần ôn lại các kiến thức của chương trình lớp 7 để áp dụng tốt trong quá trình chứng minh và suy luận chứng minh. Tuần 35 TIẾT 53 : ÔN TẬP CHƯƠNG III. Ngày soạn : 14/05/2008 I . MỤC TIÊU : Qua tiết học này HS cần đạt được : * Về kiến thức lý thuyết : Củng cố các kiến thức về tam giác đồng dạng, định lí thales, tính chất về tia phân giác của góc theo hệ thống các kiến thức theo kí hiệu và bằng lời. * Về thực hành : HS thực hiện thành thạo các dạng bài tập về định lí Thales, tính chất về tia phân giác của góc trong tam giác, các dạng tam giác đồng dạng của tam giác thường và tam giác vuông. * Về liên hệ thực tế : HS nắm bắt được các vấn đề của tam giác đồng dạng trong thực tế là rất quan trọng vì có thể tránh được nguy hiểm cho con người. II . CHUẨN BỊ CỦA THẦY VÀ TRÒ : Thầy : Giáo án điện tử, bảng phụ , phiếu học tập, các dụng cụ dạy học. Trò : SGK, các dụng cụ học tập. III . Các hoạt động dạy và học : A . Hoạt động 1 : Ổn định lớp . B . Hoạt động 2 : Kiểm tra bài cũ: HS1 : Hai tam giác vuông có những trường hợp đồng dạng nào? HS2 : Nêu dấu hiệu đặc biệt đồng dạng của hai tam giác vuông? Hai tam giác đồng dạng thì tỉ số của hai đường cao tương ứng có tỉ số thế nào? Tỉ số hai diện tích thế nào? HS3 : Hai tam giác thường có những trường hợp đồng dạng nào? Nêu nội dung mỗi dạng? C . Hoạt động 3 : Tiến hành ôn tập : Hoạt động của giáo viên & HS Nội Dung ? Hãy nhắc lại lần lượt các kiến thức lý thuyết của chương III? GV : Yêu cầu HS về nhà tóm tắt bằng kí hiệu và học theo SGK. BT 1. Hãy cho biết các khẳnh định sau đúng hay sai? a. Hai tam giác bằng nhau thì đồng dạng với nhau. b. Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng. c. Nếu theo tỉ số đồng dạng và theo tỉ số thì theo tỉ số . d. Trên hai cạnh AB, AC của lấy hai điểm M và N sao cho thì MN // BC. BT 2 : Cho tam giác ABC có AB = 6 cm, AC= 9cm, BC=12 cm, và có DE=24 cm, EF=18 cm, DF=12 cm . Hai tam giác ABC và FDE có đồng dạng với nhau không? Vì sao? Tính tỉ số chu vi của hai tam giác đó, so sánh tỉ số đó với tỉ số đồng dạng? ? Hãy vẽ hình và thực hiện bài làm? ? Có nhận xét gì cho bài làm? GV : Chốt lại. BT 3 : Bóng của một cây trên mặt đất có độ dài 15 mét, cùng thời điểm đó một thanh sắt cao 2 m có bóng trên mặt đất 1m. Tính chiều cao của cây? ? Hãy vẽ hình biểu diển cho bài toán? GV: Cây và cọc xem như vuông góc với mặt đất, khi cùng thời điểm thì các góc tạo ra như thế nào? ? Vậy hai tam giác ABC và MNP thế nào? ? Hãy trình bày bài làm? GV : chốt lại bài làm và cách làm. BT 4:Cho hình vẽ sau : MN // BC. Tính x ? . BT2 : a . vì : b . Tỉ số hai chu vi : Gọi P1 , P2 lần lượt là hai chu vi của hai tam giác ABC và DEF ta có : Do đó tỉ số hai chu vi bằng tỉ số đồng dạng. BT 3 : Gọi chiều cao cây là AB, bóng của cây là AC, chiều cao cọc là MN, bóng của cọc là MP Ta có : Nên : cm. BT 4 : Vì MN // BC nên : Theo định lí Thales ta có BT 5 : Cho tam giác ABC vuông tại A có đường cao AH, cho biết AB = 15 cm, AH = 12 cm. a . Chứng minh : . b . Tính độ dài các đoạn thẳng BH, HC, AC. c . Trên cạnh AC lấy điểm E sao cho CE = 5 cm, trên cạnh BC lấy điểm F sao cho CF = 4 cm. Chứng minh tam giác CEF vuông. d . Chứng minh : CE.CA = CF.CB? ? Hãy đọc đề vẽ hình và ghi GT/KL của bài toán? Theo hình vẽ và đề bài thì hai tam giác AHB và CHA có gì? Vậy cần phải chứng minh thêm điều gì thì có thể kết luận chúng đồng dạng với nhau? Trong các đoạn cần tính ta có thể tính đoạn nào trước dựa vào đâu? Tính đoạn CH và AC bằng cách nào? HS : trả lời có thể theo nhiều cách GV chọn cách ngắn gọn nhất để tính. ? Câu c muốn chứng minh tam giác CEF vuông thì ta có thể chứng minh gì? GV có thể gợi ý cho HS. ? Hãy trình bày chứng minh? Câu d hãy làm theo cách suy luận ngược để tìm ra tam giác đồng dạng và trình bày chứng minh? ? có nhận xét gì cho bài làm? GV : Chốt lại bài làm. Bài tập 6 : Cho tam giác ABC, AH, BK lần lượt là đường cao tại A và B. Chứng minh rằng : CK.CA = CH.CB? ? Hãy vẽ hình và ghi GT/KL của bài? Theo cách chứng minh đẳng thức trong hình học ta thường làm thế nào? Hãy trình bày cách suy luận và chứng minh? Có nhận xét gì cho bài làm? GV chốt lại bài làm. BT 5 : GT , AH đường cao AB=15 cm, AH = 12 cm E Ỵ AC, F Ỵ BC, CE = 5 cm, CF = 4 cm. KL a. b. Tính:BH, HC, AC. c. CM : vuông. d. CM:CE.CA=CF.CB. Chứng minh : . Ta có : (1) Mà : => (2) Từ 1 và 2 suy ra : (g-g) Tính BH, HC, AC? Theo định lý Pitago cho tam giác vuông AHB ta có : BH2 = AB2 – AH2 = 152 – 122 = 225 – 144 = 81 = 92 Nên : BH = 9 cm. Ta lại có : ( CMT) Nên : Chứng minh : vuông. Ta có : CÂ chung. Nên : (c-g-c) Mà vuông tại H. Suy ra : vuông tại F. (đpcm) Chứng minh : CE.CA = CF.CB. Ta có Nên : (đpcm) BT6 : GT , AH, BK là Đường cao. KL CK.CA = CH.CB Chứng minh : CK.CA = CH.CB. Xét hai tam giác : CKB và CHA ta có : => suy ra : => CK.CA = CH.CB (đpcm) D. Hoạt động 4 : Củng cố tại lớp : ? Muốn tính toán các đoạn thẵng ta có thể áp dụng những kiến thức nào? HS : ? Để chứng minh đảng thức trong tam giác ta thường làm theo cách nào? HS : GV : Trong những bài chứng minh tam giác đồng dạng ta cần phải nhìn nhận bài toán theo những điều để bài đã cho là theo góc hay theo cạnh để có thể xác định được chúng đồng dạng với nhau theo trường hợp nào rồi từ đó suy luận và chứng minh. Lưu ý : Khi chứng minh hay tính toán các đoạn thẳng ta phải bám theo đề bài về những gì đã biết tránh tình trạng áp dụng những điều chưa biết để đưa vào và cho là đã biết. E. Hoạt động 5: Hướng dẩn học về nhà : -Học các kiến thức trong chương theo SGK ở phần ôn tập. - Làm các bài tập ở phần ôn tập và xem lại các bài vừa giải trong tiết - Chuẩn bị Kiểm tra học kì II - Cần ôn bổ sung các kiến thức về định lý Pytago và các tính chất khác có liên quan như tính chất về tổng các góc trong tam giác, các tính chấtt về đường cao, đường phân giác, trung tuyến, tính chất dãy tỉ số bằng nhau, tính chất tỉ lệ thức,
Tài liệu đính kèm:
 giao_an_hinh_hoc_8_tiet_67_on_tap_cuoi_nam_ban_dep.doc
giao_an_hinh_hoc_8_tiet_67_on_tap_cuoi_nam_ban_dep.doc





