Giáo án Hình học 8 - Tiết 15 đến 16 (Bản đẹp)

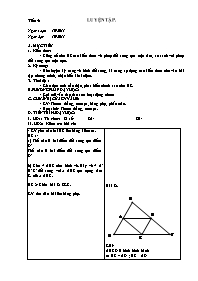
Tiết15: LUYỆN TẬP.
Ngày soạn: 	10/2011
Ngày dạy:	10/2011
A. MỤC TIÊU:
1. Kiến thức: 
	- Củng cố cho HS các kiến thức về phép đối xứng qua một tâm, so sánh với phép đối xứng qua một trục.
2. Kỹ năng: 
	- Rèn luyện kỹ năng vẽ hình đối xứng, kĩ năng áp dụng các kiến thức trên vào bài tập chứng minh, nhận biết khái niệm.
3. Thái độ : 
	- Giáo dục tính cẩn thận, phát biểu chính xác cho HS.
B.PHƯƠNG PHÁP DẠY HỌC:
	- Gợi mở vấn đáp đan xen hoạt động nhóm
C. CHUẨN BỊ CỦA GV VÀ HS: 
	- GV: Thước thẳng, com pa, bảng phụ, phấn màu.
	- Học sinh: Thước thẳng, com pa.
D. TIẾN TRÌNH DẠY HỌC: 
I. HĐ1: Tổ chức: 	Sĩ số:	8A:	8B:
II. HĐ2: Kiểm tra bài cũ:
- GV yêu cầu hai HS lên bảng kiểm tra.
HS 1: 
a) Thế nào là hai điểm đối xứng qua điểm O?
Thế nào là hai điểm đối xứng qua điểm O?
b) Cho D ABC như hình vẽ. Hãy vẽ D A' B' C' đối xứng với D ABC qua trọng tâm G của D ABC.
HS 2: Chữa bài 52 SGK.
GV đưa đầu bài lên bảng phụ.
- GV nhận xét cho điểm.
Bài 52.
Giải:
ABCD là hình bình hành
Þ BC // AD ; BC = AD
Þ BC // AE (vì D, A, E thẳng hàng) và BC = AE (= AD)
Þ Tứ giác AEBC là hình bình hành (theo dấu hiệu nhận biết)
Þ BE // AC (1) 
Chứng minh tương tự
Þ BF // AC và BF = AC (2)
Từ (1 ) (2) ta có:
E,B,F thẳng hàng theo tiên đề Ơclít và BE = BF (= AC)
Þ E đối xứng với F qua B.
Hoạt động 3
LUYỆN TẬP (23 ph)
Bài 54 tr 96 SGK.
- GV hướng dẫn HS phân tích theo sơ đồ ngược từ dưới lên. Yêu cầu HS trình bày miệng, GV ghi lại.
- Bài 56 SGK
- GV cần phân tích kĩ về tam giác đều để HS thấy rõ là tam giac đều có 3 trục đối xứng nhưng không có tâm đối xứng.
- HS quan sát hình vẽ rồi trả lời bằng miệng.
Bài 57 SGK
Bài 54.
Giải:
C và A đối xứng với nhau qua Oy Þ Oy là trung trực của CA Þ OC = OA.
Þ D OCA cân tại O, có OE ^ CA 
Þ Ô3 = Ô4 (T/C D cân)
Chứng minh tương tự
Þ OA = OB và O1 = O2
Vậy OC = OB = OA (1)
Ô3 + Ô2 = Ô4 + Ô1 = 900
Þ Ô1 + Ô2 + Ô3 + Ô4 = 1800 (2)
Từ (1) và (2) Þ O là trung điểm của CB hay C và B đối xứng nhau qua O.
Bài 56
a) Đoạn thẳng AB ;à hình có tâm đối xứng.
b) Tam giác đều ABC không có tâm đối xứng.
c) Biển cấm đi ngược chiều là hình có tâm đối xứng.
d) Biển chỉ hướng đi vòng tránh chướng ngại vật không có tâm đối xứng.
Bài 57 SGK
a) Đúng.
b) Sai 
c) Đúng vì hai tam giác đó bằng nhau.
Hoạt động 4
CỦNG CỐ (8 ph)
- GV cho HS lập bảng so sánh hai phép đối xứng.
 Đối xứng trục
 Đối xứng tâm
Hai điểm đối xứng
A và A' đối xứng nhau qua d Û d là trung trực của đoạn thẳng 
A A'.
A và A' đối xứng nhau qua O Û O là trung điểm của đoạn thẳng A A'.
Hai hình đối xứng
Hình có trục đối xứng
Hình có tâm đối xứng
Hoạt động IV
HƯỚNG DẪN VỀ NHÀ (2 ph)
- Làm các bài tập 95, 96, 97 tr 70 SBT.
- Ôn tập định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành. So sánh hai phép đối xứng để ghi nhớ.
Tiết16: 
HÌNH CHỮ NHẬT.
	Ngày soạn: 15/10/2011
	Ngày dạy: 17/10/2011
A. MỤC TIÊU:
1. Kiến thức: 
	HS hiểu định nghĩa hình chữ nhật, các tính chất của hình chữ nhật, các dấu hiệu nhận biết một tứ giác là hình chữ nhật.
2. Kỹ năng : 
	- HS biết vẽ hình chữ nhật, bước đầu biết cách chứng minh một tứ giác là hình chữ nhật. Biết vận dụng các kiến thức về hình chữ nhật áp dụng vào tam giác.
 - Bước đầu biết vận dụng các kiến thức về hình chữ nhật để tính toán, chứng minh.
3. Thái độ : 
	- Giáo dục tính cẩn thận, phát biểu chính xác cho HS.
B.PHƯƠNG PHÁP DẠY HỌC:
	- Gợi mở vấn đáp đan xen hoạt động nhóm
C. CHUẨN BỊ CỦA GV VÀ HS: 
	- GV: Thước thẳng, com pa, bảng phụ, phấn màu.Bảng vẽ sẵn một tứ giác để kiểm tra xem có là hình chữ nhật không.
	- Học sinh: Thước thẳng, com pa. Ôn tập định nghĩa tính chất, dấu hiệu nhận biết hình bình hành, hình thang cân. Ôn tập phép đối xứng trục, phép đối xứng tâm.
D. TIẾN TRÌNH DẠY HỌC: 
I. HĐ1: Tổ chức: 	Sĩ số:	8A:	8B:
II. HĐ2: Kiểm tra bài cũ:
- GV đặt vấn đề vào bài: Hình chữ nhật đã rất quen thuộc với chúng ta, hãy lấy ví dụ thực tế về hình chữ nhật.
- GV vẽ một hình chữ nhật lên bảng. Yêu cầu HS vẽ vào vở.
- H×nh ch÷ nhËt lµ mét tø gi¸c cã ®Æc ®iÓm g× vÒ gãc?
- Yªu cÇu HS tãm t¾t ®Þnh nghÜa b»ng kÝ hiÖu.
- H×nh ch÷ nhËt cã ph¶i lµ h×nh b×nh hµnh kh«ng ? Cã ph¶i lµ h×nh thang c©n kh«ng? V× sao?
- H×nh ch÷ nhËt lµ mét h×nh b×nh hµnh, lµ mét h×nh thang c©n, vËy h×nh ch÷ nhËt cã nh÷ng tÝnh chÊt g×, ta chuyÓn sang phÇn 2.
- HS lÊy vÝ dô thùc tÕ vÒ h×nh ch÷ nhËt nh­ ®­êng viÒn viªn g¹ch hoa, quyÓn s¸ch, quyÓn vë...
- H×nh ch÷ nhËt lµ mét tø gi¸c cã 4 gãc vu«ng.
- Tø gi¸c ABCD lµ h×nh ch÷ nhËt Û A = B = C = D = 900.
- H×nh ch÷ nhËt lµ mét h×nh b×nh hµnh v× cã A = C = 900 vµ B = D = 900.
- H×nh ch÷ nhËt lµ mét h×nh thang c©n v× cã: AB // DC (Theo c/m trªn vµ D = C = 900).
Hoạt động 3
2. TÍNH CHẤT (6 ph)
- Hình chữ nhật có tính chất gì?
- Kết hợp các tính chất trên, hình chữ nhật có tính chất riêng nào?
- Yêu cầu HS nêu tính chất này dưới dạng GT, KL.
Hình chữ nhật có tất cả các tính chất của hình bình hành, hình thang cân.
Trong hình chữ nhật:
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
GT ABCD là hình chữ nhật
 AC cắt BD tại O
KL OA = OB = OC = OD
Hoạt động 4
3. DẤU HIỆU NHẬN BIẾT (14 ph)
- Để nhận biết một tứ giác là hình chữ nhật, cần chứng minh tứ giác có mấy góc vuông? Vì sao?
- Một tứ giác là hình thang cân cần có thêm đều kiện về góc sẽ là hình chữ nhật?Vì sao?
- Nếu tứ giác là hình bình hành cần có thêm điều kiện gì sẽ thành hình chữ nhật?
- GV yêu cầu HS đọc lại dấu hiệu nhận biết SGK.
- GV đưa H85 SGK và GT, KL lên bảng phụ, yêu cầu HS chứng minh dấu hiệu 4.
- Tứ giác có hai góc vuông có phải là hình chữ nhật không?
- Hình thang có một góc vuông có phải là hình chữ nhật không?
- Tứ giác có hai đường chéo bằng nhau có phải là hình chữ nhật không?
- Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường có là hình chữ nhật không?
- Yêu cầu HS làm ?2.
- Yêu cầu 1 HS lên bảng kiểm tra.
* Dấu hiệu nhận biết: SGK.
HS chứng minh dấu hiệu 4 tương tự như SGK.
Cách 1: Kiểm tra nếu có:
 AB = CD ; AD = BC
Và AC = BD thì kết luận ABCD là hình chữ nhật.
Cách 2: Kiểm tra nếu có: OA = OB = OC = OD thì kết luận ABCD là hình chữ nhật.
Hoạt động 5
4. ÁP DỤNG VÀO TAM GIÁC VUÔNG (10 ph)
- GV yêu cầu HS hoạt động nhóm.
Nửa lớp làm ?3.
Nửa lớp làm ?4.
- GV phát phiếu học tập có hình vẽ sẵn cho các nhóm.
- Yêu cầu đại diện hai nhóm lên trình bày.
- GV đưa định lí tr 99 lên bảng phụ yêu cầu HS đọc lại.
- Hai định lí trên có liên quan với nhau như thế nào?
?3.
a)Tứ giác ABCD là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường, hình bình hành ABCD có A = 900 nên là hình chữ nhật.
b) ABCD là hình chữ nhật nên AD = BC. Có AM = .
c) Vậy trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
?4. a) Tứ giác ABCD là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường. Hình bình hành ABCD là hình chữ nhật vì có hai đường chéo bằng nhau.
b) ABCD là hình chữ nhật nên BAC = 900. Vậy D ABC vuông.
c) Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
- HS đọc định lí SGK.
- Là hai định lí thuận và đảo của nhau.
Hoạt động 6
CỦNG CỐ (4 ph)
- Phát biểu định nghĩa hình chữ nhật.
- Nêu các dấu hiệu nhận biết hình chữ nhật.
- Nêu các tính chất của hình chữ nhật.
- Làm bài 60 SGK.
Bài 60 
D ABC vuông có:
BC2 = AB2 + AC2 ( Đ/L Pi ta go)
BC2 = 72 + 242 
BC2 = 625
Þ BC = 25
AM = (tính chất tam giác vuông)
AM = = 12, 5 cm
Hoạt động 7
HƯỚNG DẪN VỀ NHÀ (1 ph)
- Ôn tập định nghĩa tính chất, dấu hiệu nhận biết của hình thang cân, hình bình hành, hình chữ nhật và các định lí áp dụng vào tam giác vuông.
- Làm bài 58,59,61,62 tr 99 SGK.