Đề kiểm tra môn Hình học Lớp 8 (Kèm đáp án)

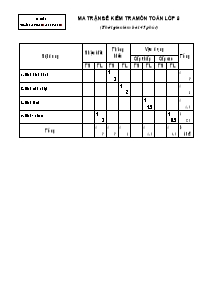
Mã đề : 
toan 8-045-1211-0124-1614-9
ma trận Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp thấp
Cấp cao
TN
TL
TN
TL
TN
TL
TN
TL
1. Hình bình hành
1
3
1
3
2. Hình chữ nhật
1
2
1
2
3. Hình thoi
1
1.5
1
1.5
4. Hình vuông 
1
3
1
0.5
2
3.5
Tổng
1
3
1
3
1
2
1
1.5
1
0.5
5
10đ
Mã đề : 
toan 8-045-1211-0124-1614-9
Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Câu 1 (3 điểm): Cho hình vẽ dưới đây, biết ABCD là hình bình hành:
	Chứng minh tứ giác AHCK là hình bình hành như sau:
	Xét hai tam giác vuông: AHD và CKB có: AD = (1) (cạnh đối của hình bình hành) ; = (2) (so le trong) (3) = DCKB (cạnh huyền - góc nhọn) (4) = CK, lại có: (5) // CK vì (6) với BD. Vậy tứ giác AHCK là hình bình hành.
	Hãy cho biết các vị trí: (1), (2), (3), (4), (5), (6) là những nội dung nào? 
Câu 2 (3 điểm): Tứ giác ở hình vẽ dưới đây là hình gì? Vì sao?
Câu 3 (4 điểm): Cho hình thoi ABCD, O là giao điểm hai đường chéo AC và BD. Từ B kẻ đường thẳng song song với đường chéo AC, Từ C kẻ đường thẳng song song với đường chéo BD. Hai đường thẳng đó cắt nhau tại E.
	a. Chứng minh tứ giác BOCE là hình chữ nhật.
	b. Tính độ dài cạnh của hình thoi biết độ dài hai đường chéo lần lượt là 24cm và 10 cm.
	c. Tìm thêm điều kiện của hình thoi ABCD để tứ giác BOCE là hình vuông.
	Ghi chú: - Có thể sử dụng máy tính bỏ túi;
	 - Giáo viên không được giải thích gì thêm!
Mã đề : 
toan 8-045-1211-0124-1614-9
đáp án Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Câu
Nội dung
Điểm
1
(1)
(2)
(3) 
(4) 
 (5) 
(6) 
BC
DAHD
AH
CK
cùng vuông góc
0.5x6
= 3 điểm
2
Tứ giác ABCD là hình vuông.
1.0 điểm
Vì ABCD có hai đường chéo bằng nhau, cắt nhau tại trung điểm của mỗi đường;
1.0 điểm
Và có hai cạnh kề bằng nhau. 
1.0 điểm
3
Hình vẽ đúng:
a
Theo giả thiết ta có: BOCE là hình bình hành;
1.0 điểm
Lại vì ABCD là hình thoi = 900; 
0.5 điểm
Vậy BOCE là hình bình hành có một góc vuông nên là hình chữ nhật.
0.5 điểm
b
Theo giả thiết ta có: BD = 10cm BO = 5cm
AC = 24cm OC = 12 cm;
0.75 điểm
áp dụng định lý Pitago trong tam giác BOC ta có:
BC2 = BO2 + OC2 = 25 + 144 = 169 BC = 13 (cm).
0.75 điểm
c
BOCE là hình vuông = 450= 900 
0.25 điểm
ABCD là hình vuông. 
0.25 điểm
Lưu ý: HS có thể làm cách khác, kết quả đúng và hợp lý vẫn cho điểm tối đa, 
vẽ hình sai không tính điểm cả câu.
Mã đề : 
toan 8-045-1212-0124-1614-0
ma trận Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng
Cấp thấp
Cấp cao
TN
TL
TN
TL
TN
TL
TN
TL
1. Hình bình hành
1
1.5
1
1.5
2. Hình chữ nhật
1
3
1
2
2
5
3. Hình thoi
1
3
1
3
4. Hình vuông 
1
0.5
1
0.5
Tổng
2
6
2
3.5
1
0.5
5
10đ
Mã đề : 
toan 8-045-1212-0124-1614-0
Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Câu 1 (3 điểm): Cho hình vẽ dưới đây:
	Chứng minh hai điểm E và F đối xứng nhau qua O như sau:
	Tứ giác AEDF có (1) nên là (2), O là (3) của (4) ị O cũng là (5) của đường chéo (6) ị hai điểm E và F đối xứng nhau qua O.
	Hãy cho biết các vị trí: (1), (2), (3), (4), (5), (6) là những nội dung nào? 
Câu 2 (3 điểm): Tứ giác ở hình vẽ dưới đây là hình gì? Vì sao?
Câu 3 (4 điểm): Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi E là trung điểm của AC; K là điểm đối xứng với M qua E. 
	1. Chứng minh AKCM là hình chữ nhật.
	2. Chứng minh tứ giác AKMB là hình bình hành.
	3. Tìm thêm điều kiện của tam giác ABC để AKCM là hình vuông.
	Ghi chú: - Có thể sử dụng máy tính bỏ túi;
	 - Giáo viên không được giải thích gì thêm!
Mã đề : 
toan 8-045-1212-0124-1614-0
đáp án Đề kiểm tra môn Toán lớp 8
(Thời gian làm bài 45 phút)
Câu
Nội dung
Điểm
1
(1)
(2)
(3) 
(4) 
 (5) 
(6) 
3 góc vuông
hình chữ nhật
trung điểm
đường chéo AD
trung điểm
EF
0.5x6
= 3 điểm
2
Tứ giác ABCD là hình thoi.
1.0 điểm
Vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường
1.0 điểm
và có đường chéo BD là phân giác của góc B.
1.0 điểm
3
Hình vẽ đúng:
a
Theo giả thiết ta có: Tứ giác AKCM có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành, 
1.0 điểm
DABC có AM là trung tuyến AM cũng là đường cao
= 900;
0.5 điểm
Vậy AKCM là hình bình hành có một góc vuông nên là hình chữ nhật.
0.5 điểm
b
Theo câu trên ta có AK // MC AK // BM (1), và có 
AK = MC, giả thiết: AM là trung tuyến của DABC 
MC = BM AK = BM (2)
0.75 điểm
Kết hợp (1) và (2) AK song song và bằng BM 
0.75 điểm
Vậy AKMB là hình bình hành.
c
AKCM là hình vuông = 450 = 450
0.25 điểm
Khi đó DABC là tam giác vuông cân tại A.
0.25 điểm
Lưu ý: HS có thể làm cách khác, kết quả đúng và hợp lý vẫn cho điểm tối đa, 
vẽ hình sai không tính điểm cả câu.