Đề kiểm tra 1 tiết môn Hình học 8 (Có ma trận và đáp án)

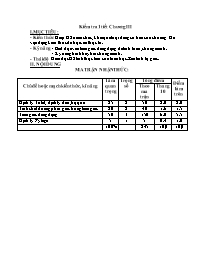
Kiểm tra 1 tiết Chương III
I.MỤC TIÊU:
- Kiến thức: Giúp HS nắm chắc, khái quát nội dung cơ bản của chương Để vận dụng kiến thức đã học vào thực tế .
- Kỹ năng: - Biết dựa vào tam giác đồng dạng để tính toán, chứng minh.
 - Kỹ năng trình bày bài chứng minh.
- Thái độ: Giáo dục HS tính thực tiễn của toán học. Rèn tính tự giác.
II. NỘI DUNG
MA TRẬN NHẬN THỨC:
Chủ đề hoặc mạch kiến thức, kĩ năng
Tầm 
quan trọng
Trọng số
Tổng điểm
Điểm
làm
tròn
Theo
ma trận
Thang
10
Định lý Ta lét, định lý đảo, hệ quả
25
2
50
2.0
2.0
Tính chất đường phân giác trong tam giác
20
2
40
1.6
1.5
Tam giác đồng dạng
50
3
150
6.0
5.5
Định lý Pytago
5
1
5
0.4
1.0
100%
245
10,0
10,0
MA TRẬN ĐỀ KIỂM TRA:
 Cấp độ
 Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Định lý Ta lét, định lý đảo, hệ quả
Bài 1
Số câu:
Điểm:
Tỉ lệ %:
1
2.0
20%
1
2.0
20%
Tính chất đường phân giác trong tam giác
Bài 2
c
Số câu:
Điểm:
Tỉ lệ %:
1
1.5
15%
1
1.5
15%
Tam giác đồng dạng
Hình vẽ
Bài 2
b
Bài 2 bài 3
D a,b
Bài 3
c
Số câu:
Điểm:
Tỉ lệ %:
1
0.5
5%
1
1.5
15%
1 2
1.0 1.5
10% 15%
1
1
10%
6
5.5
55%
4) Định lý Pytago
Hình vẽ
Bài 2
a
Số câu:
Điểm:
Tỉ lệ %:
1
0.5
5%
1
0.5
5%
1
1
10%
Tổng
Số câu:
Điểm:
Tỉ lệ %:
2
1
10%
3
4.0
40%
3
4.0
40%
1
1.0
10%
9
10.0
100%
BẢNG MÔ TẢ
Bài 1: Thông hiểu định lý talet và hệ quả 
Bài 2:
Nhận biết định lý pytago
Thông hiểu chứng minh tam giác đồng dạng
Vận dụng cấp thấp tính chất tia phân giác
Vận dụng cấp thấp tam giác đồng dạng
Bài 3:
Vận dụng cấp thấp tam giác đồng dạng
Vận dụng cấp thấp tam giác đồng dạng
Vận dụng cấp cao tam giác đồng dạng
ĐỀ KIỂM TRA 1 TIẾT
Bài 1: (2 điểm)
Bài 2: (5 điểm) 	(Hình vẽ 0.5 điểm)
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Tia phân giác góc A cắt BC tại D, vẽ đường cao AH
Tính BC	(0.5 điểm)
Chứng minh: ΔHBA ΔABC. Tính AH	(1.5 điểm)
Tính BD, DC	(1.5 điểm)
Chứng minh AH2 = HB.HC	(1 điểm)
Bài 3 : (3điểm) 	(Hình vẽ 0.5 điểm)
Cho hình bình hành ABCD, AC là đường chéo lớn. Từ C kẻ CE vuông góc AB, CF vuông góc AD ; từ B kẻ BG vuông góc AC (E; F thuộc phần kéo dài AB; AD) Chứng minh rằng : 
	a. DABG D ACE 	(0.75 điểm)
	b. DCBG DACF	(0.75 điểm)
	c. Cm AB.AE + AD.AF = AC2 	(1 điểm)
đáp án
Bài 1
2
DE//BC
Theo định lý talet => 
Theo hệ quả talet=>	
0.5
0.5
0.5
0.5
Bài 2:
5
Hình vẽ:
0.5
a. Theo pytago tính BC=10
0.5
b. DHBA DABC. Tính AH
xét DHBA và DABC có B chung
=>DHBA DABC.
=>AH=AB.AC/BC=4,8
1.5
0.5
0.5
0.5
c. Tính BD, DC
AD là phân giác=>
BD= DC=	
1.5
0.5
0.5
0.5
d. Chứng minh AH2 = HB.HC	
Xét DHBA và DHAC có góc B = góc HAC cùng phụ BHA
=>DHBA DHAC
=>
	=>HA2=HB.HC	
1.5
0.5
0.5
0.5
Bài 3: hình vẽ:
0.5
a. DABG D ACE 
góc A chung
0.75
b. DCBG DACF	
góc nhọn bằng nhau (so le trong)
0.75
c. Cm AB.AE + AD.AF = AC2
Từ a và b => tỉ số đồng dạng
Lấy tổng
1