Đề kiểm tra 1 tiết môn Đại số Lớp 8 - Tiết 21 - Trường THCS Tân Phú

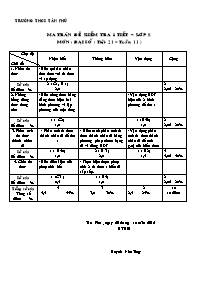
TRÖÔØNG THCS TAÂN PHUÙ
MA TRAÄN ÑEÀ KIEÅM TRA 1 TIEÁT – LÔÙP 8
MOÂN : ÑAÏI SOÁ ( Tieát 21 – Tuaàn 11 )
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
1. Nhân đa thức
- Biết qui tắc nhân đơn thức với đa thức và áp dụng
Soá caâu
Số điểm %
2 ( C1, B 1)
2,0
2
2,0đ 20%
2. Những hằng đẳng thức đáng nhớ
- Biết công thức hằng đẳng thức hiệu hai bình phương và lập phương của một tổng
- Vận dụng HĐT hiệu của 2 bình phương để tìm x
Soá caâu
Số điểm %
1 ( C2)
1,0
1 ( B4b)
1,0
2
2,0đ 20%
3. Phân tích đa thức thành nhân tử
- Phân tích đa thức thành nhân tử để tìm x
- Hiểu cách phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử và dùng HĐT
- Vận dụng phân tích đa thức thành nhân tử để tính g.trị của biểu thức
Soá caâu
Số điểm %
1 ( B4a)
1,0
2 ( B 3 )
2,0 
1 ( B2)
1,5
4
4,0đ 40%
4. Chia đa thức
- Biết điều kiện của phép chia hết
- Thực hiện được phép chia 2 đa thức 1 biến đã sắp xếp.
Soá caâu
Số điểm %
1 (C3 )
0,5
1 ( B5)
1,0
2
2,0đ 20%
Toång soá caâu
Tổng số điểm %
5
4,5 45%
3
3,0 30%
2
2,5 25% 
10
10 điểm
 Taân Phuù , ngaøy 20 thaùng 10 naêm 2012
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑEÀ KIEÅM TRA 1 TIEÁT CHÖÔNG I – LÔÙP 8
MOÂN : ÑAÏI SOÁ ( Tieát 21 – Tuaàn 11 )
I . Lyù thuyeát : (2,5 ñ) 
Caâu 1: Phát biểu qui tắc nhân đơn thức với đa thức? ( 1đ)
Caâu 2: Viết công thức hằng đẳng thức hiệu của hai bình phương và lập phương của một tổng ? ( 1ñ)
Caâu 3 : Khi nào đa thức A chia hết cho đa thức B ?. (0,5ñ)
II. Baøi taäp : (7,5 ñ)
Bài 1 : ( 1đ) 
 Làm tính nhân : 3x2 ( 2x2 – 5x + 9 )
Bài 2 : ( 1,5đ) 
 Tính giaù trò cuûa bieåu thöùc : x2 – 2xy + y2 - 81 taïi x = 93 ; y = 2 
Bài 3 : ( 2đ) 
 Phaân tích caùc ña thöùc sau thaønh nhaân töû :
 a ) x2 – y2 – 5x – 5y 
 b) x2 – 4y2+ 2x + 1 
Bài 4 : (2 ñ) 
 Tìm x bieát : a) 
 b) ( 1 - 2x )2 – ( x + 5)2 = 0
Bài 5 : (1ñ) 
 Làm tính chia 
 Taân Phuù , ngaøy 20 thaùng 10 naêm 2012
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑAÙP AÙN ÑEÀ KIEÅM TRA 1 TIEÁT – LÔÙP 8 
MOÂN : ÑAÏI SOÁ ( Tieát 21 – Tuaàn 11 )
Câu – Bài 
Ñaùp aùn
Ñieåm
1
* Muốn nhân một đơn thức với đa thức ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau
1ñ
2
 * A2 – B2 = ( A + B) ( A – B )
* ( A + B)3 = A3 + 3A2B + 3AB2 + B3
0,5ñ
0,5ñ
3
* Đa thức A chia hết cho đa thức B 0 neáu tìm ñöôïc moät đña thức Q sao cho A = B.Q 
0,5ñ
1
 3x2 ( 2x2 – 5x + 9 ) = 3x2. 2x2 - 3x2.5x + 3x2.9
 = 6x4 - 15x3 + 27x2
0,5ñ
0,5ñ
2
x2 – 2xy + y2 - 81 = ( x –y)2 – 92 = (x –y + 9 ) ( x – y -9 )
Thay x = 93 ; y = 2 vào biểu thức : (x –y + 9 ) ( x – y -9 ) 
 = (93 – 2 + 9 ) ( 93 -2 -9 )
 = 100. 82 = 8200
Vậy giá trị của biểu thức tại x = 93 ; y = 2 là: 8200
0,5ñ
0,5đ
0,25đ
0,25đ
3
a ) x2 – y2 – 5x – 5y = ( x2 – y2 ) – ( 5x + 5y)
 = (x +y ) ( x –y) - 5 ( x +y) = ( x + y ) ( x –y -5 )
b) x2 – 4y2+ 2x + 1 = ( x2 + 2x + 1 ) – 4y2 
 = ( x +1 )2 – (2y)2 = ( x +1+ 2y) ( x + 1 -2y )
0,5ñ
0,5ñ
0,5ñ
0,5ñ
4
a) 
 x( x -7) = 0 
 x = 0 Hoặc x -7 = 0 x = 7 
b) ( 1 - 2x )2 – ( x + 5)2 = 0
 ( 1 – 2x + x + 5) ( 1 - 2x – x - 5 ) = 0
 ( -x + 6 ) ( - 3x - 4 ) = 0
 - x + 6 = 0 x = 6 
Hoặc : -3x – 4 = 0 x = 
Vậy x = 6 và x = 
0,5ñ
0,5ñ
0,5ñ
0,5ñ
5
2x3 – 5x2 + 6x - 15 2x - 5
2x3 - 5x2 x2 + 3
 0x2 + 6x - 15
 6x -15
 0 
Vậy : 
0,75ñ
0,25ñ
TRÖÔØNG THCS TAÂN PHUÙ
MA TRAÄN ÑEÀ KIEÅM TRA 1 TIEÁT – LÔÙP 8
MOÂN : ÑAÏI SOÁ ( Tieát 32 – Tuaàn 16 )
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
1. Rút gọn phân thức và qui đồng mẫu thức
- Biết qui tắc qui đồng mẫu thức.
- Biết rút gọn phân thức
- Hiểu cách qui đồng mẫu thức
- Hiểu cách rút gọn phân thức
Soá caâu
Số điểm %
2 
2,0
2 
2,0
4
4,0đ 40%
2. Cộng trừ phân thức đại số
- Biết cộng 2 phân thức cùng mẫu
- Vận dụng HĐT để tìm MTC và thực hiện phép cộng 2 phân thức.
- Vận dụng qui tắc đổi dấu để tìm MTC thực hiện phép trừ 2 phân thức.
Soá caâu
Số điểm %
1 
1,5
2
3,0
3
4,5đ 45%
3. Nhân phân thức đại số
- Hiểu cách nhân 2 phân thức đại số
Soá caâu
Số điểm %
1
1,5
1
1,5đ 15%
Toång soá caâu
Tổng số điểm %
3
3,5 35%
3
3,5 35%
2
3 30% 
8
10 điểm
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑEÀ KIEÅM TRA 1 TIEÁT CHÖÔNG I – LÔÙP 8
MOÂN : ÑAÏI SOÁ ( Tieát 32 – Tuaàn 16 )
Caâu 1 : ( 2đ) a) Muốn qui đồng mẫu thức nhiều phân thức ta làm thế nào ? 
 Áp dụng : Qui đồng mẫu thức 2 phân thức sau :
Caâu 2: ( 2đ) Rút gọn phân thức
 a) 
 b ) 
Caâu 3. ( 6đ) thực hiện phép tính .
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑAÙP AÙN ÑEÀ KIEÅM TRA 1 TIEÁT – LÔÙP 8 
MOÂN : ÑAÏI SOÁ ( Tieát 32 – Tuaàn 16 )
Caâu
Ñaùp aùn
Ñieåm
 1
a) Muốn qui đồng mẫu thức nhiều phân thức ta có thể làm như sau :
- Phân tích mẫu thức thành nhân tử rồi tìm MTC.
- Tìm nhân tử phụ của mỗi mẫu thức.
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
1đ
b) * x2 – 9 = ( x + 3 )( x – 3 )
* MTC: 2x ( x -3) ( x + 3)
* 
* 
0,5ñ
0,5ñ
2
 a) 
1,0ñ
b ) 
1,0ñ
3
1,5ñ
0,5ñ
0,5đ
0,5ñ
0,5ñ
0,5ñ
0,5ñ
d) 
0,75ñ
0,75ñ
TRÖÔØNG THCS TAÂN PHUÙ
MA TRẬN ÑEÀ KIEÅM TRA 1 TIEÁT CHƯƠNG III – LÔÙP 8 
MOÂN : ÑAÏI SOÁ ( Tieát 56 – Tuaàn27 )
 Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
1. Khái niệm phương trình tương đương
- Biết khái niệm 2 phương trình tương đương và áp dụng
Số câu
Số điểm %
2 
2,0
2
2,0đ 20%
2. Phương trình bậc nhất 1 ẩn 
- Biết giải phương trình bậc nhất 1 ẩn dạng đơn giản
- Hiểu cách giải phương trình bậc nhất có mẫu số, chứa ẩn ở mẫu và ph. trình tích.
Số câu
Số điểm %
1 
1,5
3
4,5
4
6,0đ 60%
3. Giải bài toán bằng cách lập phương trình
- Vận dụng công thức tính chu vi hình chữ nhật để giải bài toán bằng cách lập ph. Trình.
Số câu
Số điểm %
1
2,0
1
2,0đ 20%
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑEÀ KIEÅM TRA 1 TIEÁT CHƯƠNG III – LÔÙP 8 
MOÂN : ÑAÏI SOÁ ( Tieát 56 – Tuaàn27 )
Câu 1 : ( 2đ) a)Thế nào là 2 phương trình tương đương ? 
 b) Áp dụng : Hai phương trình sau có tương đương không ? vì sao ?
 x - 3 = 0 ; 2x = 6 
Câu 2: ( 6 đ)Giải các phương trình sau:
 a) 2( x +3 ) - ( 3x - 5 ) = 4( x - 1 ) ( 1,5đ)
 b) ( 2x + 1 ) ( x -3 ) = ( x -3 ) ( x + 4 ) ( 1,5đ)
 c) ( 1,5đ)
 d) ( 1,5đ)	
Câu 3. ( 2đ) Một hình chữ nhật có chiều dài lớn hơn chiều rộng là 6cm và chu vi của nó là 88cm.Tính diện tích hình chữ nhật đó.
 GVBM
 Huyønh Nhu Thuïy
TRÖÔØNG THCS TAÂN PHUÙ
ÑAÙP AÙN ÑEÀ KIEÅM TRA 1 TIEÁT – LÔÙP 8 
MOÂN : ÑAÏI SOÁ ( Tieát 56 – Tuaàn27 )
Câu
Đáp án
Điểm
 1
a) Hai phương trình được gọi là tương đương nếu chúng có cùng tập hợp nghiệm.
1đ
Phương trình : x – 3 = 0 2x = 6 
vì chúng có cùng tập nghiệm : 
 0,5đ
 0,5đ
2
2( x +3 ) - ( 3x - 5 ) = 4( x - 1 )
 2x + 6 – 3x + 5 = 4x – 4
 -x – 4x = -4 - 11 = -15
 - 5x = -15
 x = 3
Vậy: 
0,5đ
0,5đ
0,25đ
0,25đ
( 2x + 5 ) ( x -3 ) = ( x -3 ) ( x + 4 ) 
 ( 2x + 5 ) ( x -3 ) – ( x -3)( x + 4 ) = 0
 ( x -3)( 2x + 5 – x – 4 ) = 0
 ( x -3)( x + 1 ) = 0 
 x – 3 = 0 x = 3
Hoặc : x + 1 = 0 x = -1 
Vậy : 
0,5đ
0,5đ
0,25đ
0,25đ
Vậy : 
0,5đ
0,5đ
0,25đ
0,25đ
d) ĐKXĐ: 
 (Không thỏa mãn ĐKXĐ)
Vậy, phương trình (1) vô nghiệm
0,5đ
0,5đ
0,25đ
0,25đ
3
Gọi là chiều dài hình chữ nhật : x > 6
Khi đó, chiều rộng của hình chữ nhật 
Do chu vi là 88cm nên ta có ptr:	
Giải ptr: 
 (nhận)	
Vậy, chiều dài: 
Chiều rộng: 
Do đó diện tích của hình chữ nhật: 
0,5đ
0,5đ
0,5đ
0,5đ
 GVBM
 Huyønh Nhu Thuïy