Đề cương tổng hợp các dạng Toán thi vào Lớp 10 - Trường THCS Đồng Thịnh
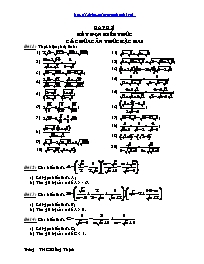
I.Điểm thuộc đường – đường đi qua điểm.
Điểm A(xA; yA) thuộc đồ thị hàm số y = f(x) yA = f(xA).
Ví dụ 1: Tìm hệ số a của hàm số: y = ax2 biết đồ thị hàm số của nó đi qua điểm A(2;4).
Giải:
Do đồ thị hàm số đi qua điểm A(2;4) nên: 4= a.22 a = 1
Ví dụ 2: Trong mặt phẳng tọa độ cho A(-2;2) và đường thẳng (d) có phương trình: y = -2(x + 1). Đường thẳng (d) có đi qua A không?
Giải:
Ta thấy -2.(-2 + 1) = 2 nên điểm A thuộc v ào đường thẳng (d)
II.Cách tìm giao điểm của hai đường y = f(x) và y = g(x).
Bước 1: Tìm hoành độ giao điểm là nghiệm của phương trình f(x) = g(x) (II)
Bước 2: Lấy nghiệm đó thay vào 1 trong hai công thức y = f(x) hoặc y = g(x) để tìm tung độ giao điểm.
Bạn đang xem 20 trang mẫu của tài liệu "Đề cương tổng hợp các dạng Toán thi vào Lớp 10 - Trường THCS Đồng Thịnh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
D¹ng I: rót gän biÓu thøc Cã chøa c¨n thøc bËc hai Bµi 1: Thùc hiÖn phÐp tÝnh: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) ; 17) ; 18) ; 19) 20) . Bµi 2: Cho biÓu thøc Rót gän biÓu thøc A; T×m gi¸ trÞ cña x ®Ó A > - 6. Bµi 3: Cho biÓu thøc Rót gän biÓu thøc B; T×m gi¸ trÞ cña x ®Ó A > 0. Bµi 4: Cho biÓu thøc Rót gän biÓu thøc C; T×m gi¸ trÞ cña x ®Ó C < 1. Bµi 5: Rót gän biÓu thøc : a) ; b) ; c) ; d) Bµi 6: Cho biÓu thøc Rót gän biÓu thøc M; So s¸nh M víi 1. Bµi 7: Cho c¸c biÓu thøc vµ Rót gän biÓu thøc P vµ Q; T×m gi¸ trÞ cña x ®Ó P = Q. Bµi 8: Cho biÓu thøc Rót gän biÓu thøc P So s¸nh P víi 5. Víi mäi gi¸ trÞ cña x lµm P cã nghÜa, chøng minh biÓu thøc chØ nhËn ®óng mét gi¸ trÞ nguyªn. Bµi 9: Cho biÓu thøc T×m ®iÒu kiÖn ®Ó P cã nghÜa, rót gän biÓu thøc P; T×m c¸c sè tù nhiªn x ®Ó lµ sè tù nhiªn; TÝnh gi¸ trÞ cña P víi x = 4 – 2. Bµi 10: Cho biÓu thøc : Rót gän biÓu thøc P; T×m x ®Ó . D¹ng II CÁC BÀI TOÁN VỀ HÀM SỐ VÀ ĐỒ THỊ I.Điểm thuộc đường – đường đi qua điểm. Điểm A(xA; yA) thuộc đồ thị hàm số y = f(x) yA = f(xA). Ví dụ 1: Tìm hệ số a của hàm số: y = ax2 biết đồ thị hàm số của nó đi qua điểm A(2;4). Giải: Do đồ thị hàm số đi qua điểm A(2;4) nên: 4= a.22 a = 1 Ví dụ 2: Trong mặt phẳng tọa độ cho A(-2;2) và đường thẳng (d) có phương trình: y = -2(x + 1). Đường thẳng (d) có đi qua A không? Giải: Ta thấy -2.(-2 + 1) = 2 nên điểm A thuộc v ào đường thẳng (d) II.Cách tìm giao điểm của hai đường y = f(x) và y = g(x). Bước 1: Tìm hoành độ giao điểm là nghiệm của phương trình f(x) = g(x) (II) Bước 2: Lấy nghiệm đó thay vào 1 trong hai công thức y = f(x) hoặc y = g(x) để tìm tung độ giao điểm. Chú ý: Số nghiệm của phương trình (II) là số giao điểm của hai đường trên. III.Quan hệ giữa hai đường thẳng. Xét hai đường thẳng : (d1) : y = a1x + b1. (d2) : y = a2x + b2. (d1) cắt (d2) a1 a2. d1) // (d2) d1) (d2) (d1) (d2) a1 a2 = -1 IV.Tìm điều kiện để 3 đường thẳng đồng qui. Bước 1: Giải hệ phương trình gồm hai đường thẳng không chứa tham số để tìm (x;y). Bước 2: Thay (x;y) vừa tìm được vào phương trình còn lại để tìm ra tham số . V.Quan hệ giữa (d): y = ax + b và (P): y = cx2 (c0). 1.Tìm tọa độ giao điểm của (d) và (P). Bước 1: Tìm hoành độ giao điểm là nghiệm của phương trình: cx2= ax + b (V) Bước 2: Lấy nghiệm đó thay vào 1 trong hai công thức y = ax +b hoặc y = cx2 để tìm tung độ giao điểm. Chú ý: Số nghiệm của phương trình (V) là số giao điểm của (d) và (P). 2.Tìm điều kiện để (d) và (P). a) (d) và (P) cắt nhau phương trình (V) có hai nghiệm phân biệt. b) (d) và (P) tiếp xúc với nhau phương trình (V) có nghiệm kép. c) (d) và (P) không giao nhau phương trình (V) vô nghiệm . VI.Viết phương trình đường thẳng y = ax + b biết. 1.Quan hệ về hệ số góc và đi qua điểm A(x0;y0) Bước 1: Dựa vào quan hệ song song hay vuông góc tìm hệ số a. Bước 2: Thay a vừa tìm được và x0;y0 vào công thức y = ax + b để tìm b. 2.Biết đồ thị hàm số đi qua điểm A(x1;y1) và B(x2;y2). Do đồ thị hàm số đi qua điểm A(x1;y1) và B(x2;y2) nên ta có hệ phương trình: Giải hệ phương trình tìm a,b. 3.Biết đồ thị hàm số đi qua điểm A(x0;y0) và tiếp xúc với (P): y = cx2 (c0). +) Do đường thẳng đi qua điểm A(x0;y0) nên có phương trình : y0 = ax0 + b (3.1) +) Do đồ thị hàm số y = ax + b tiếp xúc với (P): y = cx 2 (c0) nên: Pt: cx2 = ax + b có nghiệm kép (3.2) +) Giải hệ gồm hai phương trình trên để tìm a,b. VII.Chứng minh đường thẳng luôn đi qua 1 điểm cố định ( giả sử tham số là m). +) Giả sử A(x0;y0) là điểm cố định mà đường thẳng luôn đi qua với mọi m, thay x0;y0 vào phương trình đường thẳng chuyển về phương trình ẩn m hệ số x0;y0 nghiệm đúng với mọi m. +) Đồng nhất hệ số của phương trình trên với 0 giải hệ tìm ra x0;y0. VIII.Một số ứng dụng của đồ thị hàm số. 1.Ứng dụng vào phương trình. 2.Ứng dụng vào bài toán cực trị. bµi tËp vÒ hµm sè. Bµi tËp 1. cho parabol y= 2x2. (p) a. t×m hoµnh ®é giao ®iÓm cña (p) víi ®êng th¼ng y= 3x-1. b. t×m to¹ ®é giao ®iÓm cña (p) víi ®êng th¼ng y=6x-9/2. c. t×m gi¸ trÞ cña a,b sao cho ®êng th¼ng y=ax+b tiÕp xóc víi (p) vµ ®i qua A(0;-2). d. t×m ph¬ng tr×nh ®êng th¼ng tiÕp xóc víi (p) t¹i B(1;2). e. biÖn luËn sè giao ®iÓm cña (p) víi ®êng th¼ng y=2m+1. ( b»ng hai ph¬ng ph¸p ®å thÞ vµ ®¹i sè). f. cho ®êng th¼ng (d): y=mx-2. T×m m ®Ó +(p) kh«ng c¾t (d). +(p)tiÕp xóc víi (d). t×m to¹ ®é ®iÓm tiÕp xóc ®ã? + (p) c¾t (d) t¹i hai ®iÓm ph©n biÖt. +(p) c¾t (d). Bµi tËp 2. cho hµm sè (p): y=x2 vµ hai ®iÓm A(0;1) ; B(1;3). a. viÕt ph¬ng tr×nh ®êng th¼ng AB. t×m to¹ ®é giao ®iÓm AB víi (P) ®· cho. b. viÕt ph¬ng tr×nh ®êng th¼ng d song song víi AB vµ tiÕp xóc víi (P). c. viÕt ph¬ng tr×nh ®êng th¼ng d1 vu«ng gãc víi AB vµ tiÕp xóc víi (P). d. chøng tá r»ng qua ®iÓm A chØ cã duy nhÊt mét ®êng th¼ng c¾t (P) t¹i hai ®iÓm ph©n biÖt C,D sao cho CD=2. Bµi tËp 3. Cho (P): y=x2 vµ hai ®êng th¼ng a,b cã ph¬ng tr×nh lÇn lît lµ y= 2x-5 y=2x+m a. chøng tá r»ng ®êng th¼ng a kh«ng c¾t (P). b. t×m m ®Ó ®êng th¼ng b tiÕp xóc víi (P), víi m t×m ®îc h·y: + Chøng minh c¸c ®êng th¼ng a,b song song víi nhau. + t×m to¹ ®é tiÕp ®iÓm A cña (P) víi b. + lËp ph¬ng tr×nh ®êng th¼ng (d) ®i qua A vµ cã hÖ sè gãc b»ng -1/2. t×m to¹ ®é giao ®iÓm cña (a) vµ (d). Bµi tËp 4. cho hµm sè (P) a. vÏ ®å thÞ hµm sè (P). b. víi gi¸ trÞ nµo cña m th× ®êng th¼ng y=2x+m (d) c¾t ®å thÞ (P) t¹i hai ®iÓm ph©n biÖt A,B. khi ®ã h·y t×m to¹ ®é hai ®iÓm A vµ B. c. tÝnh tæng tung ®é cña c¸c hoµnh ®é giao ®iÓm cña (P) vµ (d) theo m. Bµi tËp5. cho hµm sè y=2x2 (P) vµ y=3x+m (d) khi m=1, t×m to¹ ®é c¸c giao ®iÓm cña (P) vµ (d). tÝnh tæng b×nh ph¬ng c¸c hoµnh ®é giao ®iÓm cña (P) vµ (d) theo m. t×m mèi quan hÖ gi÷a c¸c hoµnh ®é giao ®iÓm cña (P) vµ (d) ®éc lËp víi m. Bµi tËp 6. cho hµm sè y=-x2 (P) vµ ®êng th¼ng (d) ®I qua N(-1;-2) cã hÖ sè gãc k. a. chøng minh r»ng víi mäi gi¸ trÞ cña k th× ®êng th¼ng (d) lu«n c¾t ®å thÞ (P) t¹i hai ®iÓm A,B. t×m k cho A,B n»m vÒ hai phÝa cña trôc tung. b. gäi (x1;y1); (x2;y2) lµ to¹ ®é cña c¸c ®iÓm A,B nãi trªn, t×m k cho tæng S=x1+y1+x2+y2 ®¹t gi¸ trÞ lín nhÊt. Bµi tËp7. cho hµm sè y= t×m tËp x¸c ®Þnh cña hµm sè. t×m y biÕt: + x=4 + x=(1- )2 + x=m2-m+1 + x=(m-n)2 c¸c ®iÓm A(16;4) vµ B(16;-4), ®iÓm nµo thuéc ®å thÞ hµm sè, ®iÓm nµo kh«ng thuéc ®å thÞ hµm sè? t¹i sao. kh«ng vÏ ®å thÞ h·y t×m hoµnh ®é giao ®iÓm cña ®å thÞ hµm sè ®· cho víi ®å thÞ hµm sè y= x-6 Bµi tËp 8. cho hµm sè y=x2 (P) vµ y=2mx-m2+4 (d) a.t×m hoµnh ®é cña c¸c ®iÓm thuéc (P) biÕt tung ®é cña chóng y=(1- )2. b.chøng minh r»ng (P) víi (d) lu«n c¾t nhau t¹i 2 ®iÓm ph©n biÖt. t×m to¹ ®é giao ®iÓm cña chóng. víi gi¸ trÞ nµo cña m th× tæng c¸c tung ®é cña chóng ®¹t gi¸ trÞ nhá nhÊt. Bµi tËp 9. cho hµm sè y= mx-m+1 (d). chøng tá r»ng khi m thay ®æi th× ®êng th¼ng (d) lu«n ®I qua ®iÓm cè ®Þnh. t×m ®iÓm cè ®Þnh Êy. t×m m ®Ó (d) c¾t (P) y=x2 t¹i 2 ®iÓm ph©n biÖt A vµ B, sao cho AB= . Bµi tËp 10. trªn hÖ trôc to¹ ®é Oxy cho c¸c ®iÓm M(2;1); N(5;-1/2) vµ ®êng th¼ng (d) y=ax+b. t×m a vµ b ®Ó ®êng th¼ng (d) ®I qua c¸c ®iÓm M, N. x¸c ®Þnh to¹ ®é giao ®iÓm cña ®êng th¼ng MN víi c¸c trôc Ox, Oy. Bµi tËp 11. cho hµm sè y=x2 (P) vµ y=3x+m2 (d). chøng minh víi bÊt kú gi¸ trÞ nµo cña m ®êng th¼ng (d) lu«n c¾t (P) t¹i 2 ®iÓm ph©n biÖt. gäi y1, y2 kµ c¸c tung ®é giao ®iÓm cña ®êng th¼ng (d) vµ (P) t×m m ®Ó cã biÓu thøc y1+y2= 11y1.y2 bµi tËp 12. cho hµm sè y=x2 (P). vÏ ®å thÞ hµm sè (P). trªn (P) lÊy 2 ®iÓm A, B cã hoµnh ®é lÇn lît lµ 1 vµ 3. h·y viÕt ph¬ng tr×nh ®êng th¼ng AB. lËp ph¬ng tr×nh ®êng trung trùc (d) cña ®o¹n th¼ng AB. t×m to¹ ®é giao ®iÓm cña (d) vµ (P). Bµi tËp 13.. a. viÕt ph¬ng tr×nh ®êng th¼ng tiÕp xóc víi (P) y=2x2 t¹i ®iÓm A(-1;2). b. cho hµm sè y=x2 (P) vµ B(3;0), t×m ph¬ng tr×nh tho¶ m·n ®iÒu kiÖn tiÕp xóc víi (P) vµ ®i qua B. c. cho (P) y=x2. lËp ph¬ng tr×nh ®êng th¼ng ®i qua A(1;0) vµ tiÕp xóc víi (P). d. cho (P) y=x2 . lËp ph¬ng tr×nh d song song víi ®êng th¼ng y=2x vµ tiÕp xóc víi (P). e. viÕt ph¬ng tr×nh ®êng th¼ng song song víi ®êng th¼ng y=-x+2 vµ c¾t (P) y=x2 t¹i ®iÓm cã hoµnh ®é b»ng (-1). f. viÕt ph¬ng tr×nh ®êng th¼ng vu«ng gãc víi (d) y=x+1 vµ c¾t (P) y=x2 t¹i ®iÓm cã tung ®é b»ng 9. D¹ng III: HÖ ph¬ng tr×nh Baøi 1: : Gi¶i c¸c HPT sau: 1.1. a. b. Gi¶i: a. Dïng PP thÕ: Vaäy HPT ®· cho cã nghiÖm lµ: Dïng PP céng: Vaäy HPT ®· cho cã nghiÖm lµ: §Ó gi¶I lo¹i HPT nµy ta thêng sö dông PP céng cho thuËn lîi. Vaäy HPT cã nghiÖm lµ §èi víi HPT ë d¹ng nµy ta cã thÓ sö dông hai c¸ch gi¶I sau ®©y: 1.2. + C¸ch 1: Sö dông PP céng. §K: . Vaäy HPT cã nghiÖm lµ + C¸ch 2: Sö dông PP ®Æt Èn phô. §K: . §Æt ; . HPT ®· cho trë thµnh: (TM§K) Vaäy HPT cã nghiÖm lµ Lu ý: - NhiÒu em cßn thiÕu §K cho nh÷ng HPT ë d¹ng nµy. - Cã thÓ thö l¹i nghiÖm cña HPT võa gi¶i. Baøi 2: Giaûi caùc heä phöông trình sau (baèng pp theá) 1.1: 1.2. Baøi 3: Giaûi caùc heä phöông trình sau (baèng pp coäng ñaïi soá) 2.1. 2.2. Baøi 4: Giaûi heä phöông trình trong moãi tröôøng hôïp sau a) m = -1 b) m = 0 c) m = 1 Baøi 5: a) Xaùc ñònh heä soá avaøb, bieát raèng heä phöông trìnhcoù nghieäm laø (1; -2) b) Cuõng hoûi nhö vaäy neáu heä phöông trình coù nghieäm Baøi 6: Giaûi heä phöông trình sau: Töø ñoù suy ra nghieäm cuûa heä phöông trình Baøi 7: Giaûi caùc heä phöông trình sau: ; ; ; ; ; ; ; ; ; Bµi 8: Cho hÖ ph¬ng tr×nh Gi¶i hÖ khi a=3 ; b=-2 T×m a;b ®Ó hÖ cã nghiÖm lµ (x;y)=( Bµi 9: Gi¶I c¸c hÖ ph¬ng tr×nh sau a) b) c) (®k x;y2 ) ; ; ; ; ; ; . ; ; ; ; ; Gi¶i bµi to¸n b»ng c¸ch lËp hÖ ph¬ng tr×nh. I, Môc tiªu: * KiÕn thøc: HS gi¶i ®îc c¸c bµi to¸n thùc tÕ b»ng c¸ch lËp HPT. * KÜ n¨ng: - HS ®îc cñng cè kÜ n¨ng ph©n tÝch t×m lêi gi¶i, tr×nh bµy lêi gi¶i bµi to¸n b»ng c¸ch lËp HPT. * Th¸i ®é: RÌn tÝnh cÈn thËn, chÝnh x¸c, l« gÝc chÆt chÏ, râ rµng. II, LÝ thuyÕt cÇn nhí: * Bíc 1: + LËp HPT - Chän Èn, t×m ®¬n vÞ vµ §K cho Èn. - BiÓu diÔn mèi quan hÖ cßn l¹i qua Èn vµ c¸c ®¹i lîng ®· biÕt. - LËp HPT. * Bíc 2: Gi¶i HPT. * Bíc 3: §èi chiÕu víi §K ®Ó tr¶ lêi. III, Bµi tËp vµ híng dÉn: Bµi 1. Hai « t« cïng khëi hµnh mét lóc tõ hai tØnh A vµ B c¸ch nhau 160 km, ®i ngîc chiÒu nhau vµ gÆp nhau sau 2 giê. T×m vËn tèc cña mçi « t« biÕt r»ng nÕu « t« ®i tõ A t¨ng vËn tèc thªm 10 km/h sÏ b»ng hai lÇn vËn tèc «t« ®i tõ B. Bµi 2. Mét ngêi ®i xe m¸y ®i tõ A ®Õn B trong mét thêi gian dù ®Þnh. NÕu vËn tèc t¨ng14 km/h th× ®Õn B sím h¬n 2 giê. nÕu vËn tèc gi¶m 2 km/h th× ®Õn B muén 1 giê. TÝnh qu·ng ®êng AB, vËn tèc vµ thêi gian dù ®Þnh. Bµi 3. Ha ... 0 hay ÐFAC = 450 (2). Tõ (1) vµ (2) suy ra DFBC lµ tam gi¸c vu«ng c©n t¹i F. 3. Theo trªn ÐBFC = 900 => ÐCFM = 900 ( v× lµ hai gãc kÒ bï); ÐCDM = 900 (t/c h×nh vu«ng). => ÐCFM + ÐCDM = 1800 mµ ®©y lµ hai gãc ®èi nªn tø gi¸c CDMF néi tiÕp mét ®êng trßn suy ra ÐCDF = ÐCMF , mµ ÐCDF = 450 (v× AEDC lµ h×nh vu«ng) => ÐCMF = 450 hay ÐCMB = 450. Ta còng cã ÐCEB = 450 (v× AEDC lµ h×nh vu«ng); ÐBKC = 450 (v× ABHK lµ h×nh vu«ng). Nh vËy K, E, M cïng nh×n BC díi mét gãc b»ng 450 nªn cïng n»m trªn cung chøa gãc 450 dùng trªn BC => 5 ®iÓm b, k, e, m, c cïng n»m trªn mét ®êng trßn. 4. DCBM cã ÐB = 450 ; ÐM = 450 => ÐBCM =450 hay MC ^ BC t¹i C => MC lµ tiÕp tuyÕn cña ®êng trßn ngo¹i tiÕp tam gi¸c ABC. Bµi 24. Cho tam gi¸c nhän ABC cã ÐB = 450 . VÏ ®êng trßn ®êng kÝnh AC cã t©m O, ®êng trßn nµy c¾t BA vµ BC t¹i D vµ E. Chøng minh AE = EB. Gäi H lµ giao ®iÓm cña CD vµ AE, Chøng minh r»ng ®êng trung trùc cña ®o¹n HE ®i qua trung ®iÓm I cña BH. Chøng minh OD lµ tiÕp tuyÕn cña ®êng trßn ngo¹i tiÕp tam gi¸c BDE. Lêi gi¶i: 1. ÐAEC = 900 (néi tiÕp ch¾n nöa ®êng trßn ) => ÐAEB = 900 ( v× lµ hai gãc kÒ bï); Theo gi¶ thiÕt ÐABE = 450 => DAEB lµ tam gi¸c vu«ng c©n t¹i E => EA = EB. 2. Gäi K lµ trung ®iÓm cña HE (1) ; I lµ trung ®iÓm cña HB => IK lµ ®êng trung b×nh cña tam gi¸c HBE => IK // BE mµ ÐAEC = 900 nªn BE ^ HE t¹i E => IK ^ HE t¹i K (2). Tõ (1) vµ (2) => IK lµ trung trùc cña HE . VËy trung trùc cña ®o¹n HE ®i qua trung ®iÓm I cña BH. 3. theo trªn I thuéc trung trùc cña HE => IE = IH mµ I lµ trung ®iÓm cña BH => IE = IB. Ð ADC = 900 (néi tiÕp ch¾n nöa ®êng trßn ) => ÐBDH = 900 (kÒ bï ÐADC) => tam gi¸c BDH vu«ng t¹i D cã DI lµ trung tuyÕn (do I lµ trung ®iÓm cña BH) => ID = 1/2 BH hay ID = IB => IE = IB = ID => I lµ t©m ®êng trßn ngo¹i tiÕp tam gi¸c BDE b¸n kÝnh ID. Ta cã DODC c©n t¹i O (v× OD vµ OC lµ b¸n kÝnh ) => ÐD1 = ÐC1. (3) DIBD c©n t¹i I (v× ID vµ IB lµ b¸n kÝnh ) => ÐD2 = ÐB1 . (4) Theo trªn ta cã CD vµ AE lµ hai ®êng cao cña tam gi¸c ABC => H lµ trùc t©m cña tam gi¸c ABC => BH còng lµ ®êng cao cña tam gi¸c ABC => BH ^ AC t¹i F => DAEB cã ÐAFB = 900 . Theo trªn DADC cã ÐADC = 900 => ÐB1 = ÐC1 ( cïng phô ÐBAC) (5). Tõ (3), (4), (5) =>ÐD1 = ÐD2 mµ ÐD2 +ÐIDH =ÐBDC = 900=> ÐD1 +ÐIDH = 900 = ÐIDO => OD ^ ID t¹i D => OD lµ tiÕp tuyÕn cña ®êng trßn ngo¹i tiÕp tam gi¸c BDE. Bµi 25. Cho ®êng trßn (O), BC lµ d©y bÊt k× (BC< 2R). KÎ c¸c tiÕp tuyÕn víi ®êng trßn (O) t¹i B vµ C chóng c¾t nhau t¹i A. Trªn cung nhá BC lÊy mét ®iÓm M råi kÎ c¸c ®êng vu«ng gãc MI, MH, MK xuèng c¸c c¹nh t¬ng øng BC, AC, AB. Gäi giao ®iÓm cña BM, IK lµ P; giao ®iÓm cña CM, IH lµ Q. 1. Chøng minh tam gi¸c ABC c©n. 2. C¸c tø gi¸c BIMK, CIMH néi tiÕp . 3. Chøng minh MI2 = MH.MK. 4. Chøng minh PQ ^ MI. Lêi gi¶i: 1. Theo tÝnh chÊt hai tiÕp tuyÕn c¾t nhau ta cã AB = AC => DABC c©n t¹i A. 2. Theo gi¶ thiÕt MI ^ BC => ÐMIB = 900; MK ^ AB => ÐMKB = 900. => ÐMIB + ÐMKB = 1800 mµ ®©y lµ hai gãc ®èi => tø gi¸c BIMK néi tiÕp * ( Chøng minh tø gi¸c CIMH néi tiÕp t¬ng tù tø gi¸c BIMK ) 3. Theo trªn tø gi¸c BIMK néi tiÕp => ÐKMI + ÐKBI = 1800; tø gi¸c CHMI néi tiÕp => ÐHMI + ÐHCI = 1800. mµ ÐKBI = ÐHCI ( v× tam gi¸c ABC c©n t¹i A) => ÐKMI = ÐHMI (1). Theo trªn tø gi¸c BIMK néi tiÕp => ÐB1 = ÐI1 ( néi tiÕp cïng ch¾n cung KM); tø gi¸c CHMI néi tiÕp => ÐH1 = ÐC1 ( néi tiÕp cïng ch¾n cung IM). Mµ ÐB1 = ÐC1 ( = 1/2 s® ) => ÐI1 = ÐH1 (2). Tõ (1) vµ (2) => DMKI DMIH => => MI2 = MH.MK 4. Theo trªn ta cã ÐI1 = ÐC1; còng chøng minh t¬ng tù ta cã ÐI2 = ÐB2 mµ ÐC1 + ÐB2 + ÐBMC = 1800 => ÐI1 + ÐI2 + ÐBMC = 1800 hay ÐPIQ + ÐPMQ = 1800 mµ ®©y lµ hai gãc ®èi => tø gi¸c PMQI néi tiÕp => ÐQ1 = ÐI1 mµ ÐI1 = ÐC1 => ÐQ1 = ÐC1 => PQ // BC ( v× cã hai gãc ®ång vÞ b»ng nhau) . Theo gi¶ thiÕt MI ^BC nªn suy ra IM ^ PQ. Bµi 26. Cho ®êng trßn (O), ®êng kÝnh AB = 2R. VÏ d©y cung CD ^ AB ë H. Gäi M lµ ®iÓm chÝnh gi÷a cña cung CB, I lµ giao ®iÓm cña CB vµ OM. K lµ giao ®iÓm cña AM vµ CB. Chøng minh : 1. 2. AM lµ tia ph©n gi¸c cña ÐCMD. 3. Tø gi¸c OHCI néi tiÕp 4. Chøng minh ®êng vu«ng gãc kÎ tõ M ®Õn AC còng lµ tiÕp tuyÕn cña ®êng trßn t¹i M. Lêi gi¶i: 1. Theo gi¶ thiÕt M lµ trung ®iÓm cña => => ÐCAM = ÐBAM (hai gãc néi tiÕp ch¾n hai cung b»ng nhau) => AK lµ tia ph©n gi¸c cña gãc CAB => ( t/c tia ph©n gi¸c cña tam gi¸c ) 2. (HD) Theo gi¶ thiÕt CD ^ AB => A lµ trung ®iÓm cña => ÐCMA = ÐDMA => MA lµ tia ph©n gi¸c cña gãc CMD. 3. (HD) Theo gi¶ thiÕt M lµ trung ®iÓm cña => OM ^ BC t¹i I => ÐOIC = 900 ; CD ^ AB t¹i H => ÐOHC = 900 => ÐOIC + ÐOHC = 1800 mµ ®©y lµ hai gãc ®èi => tø gi¸c OHCI néi tiÕp 4. KÎ MJ ^ AC ta cã MJ // BC ( v× cïng vu«ng gãc víi AC). Theo trªn OM ^ BC => OM ^ MJ t¹i J suy ra MJ lµ tiÕp tuyÕn cña ®êng trßn t¹i M. Bµi 27 Cho ®êng trßn (O) vµ mét ®iÓm A ë ngoµi ®êng trßn . C¸c tiÕp tuyÕn víi ®êng trßn (O) kÎ tõ A tiÕp xóc víi ®êng trßn (O) t¹i B vµ C. Gäi M lµ ®iÓm tuú ý trªn ®êng trßn ( M kh¸c B, C), tõ M kÎ MH ^ BC, MK ^ CA, MI ^ AB. Chøng minh : Tø gi¸c ABOC néi tiÕp. 2. ÐBAO = Ð BCO. 3. DMIH ~ DMHK. 4. MI.MK = MH2. Lêi gi¶i: (HS tù gi¶i) Tø gi¸c ABOC néi tiÕp => ÐBAO = Ð BCO (néi tiÕp cïng ch¾n cung BO). Theo gi¶ thiÕt MH ^ BC => ÐMHC = 900; MK ^ CA => ÐMKC = 900 => ÐMHC + ÐMKC = 1800 mµ ®©y lµ hai gãc ®èi => tø gi¸c MHCK néi tiÕp => ÐHCM = ÐHKM (néi tiÕp cïng ch¾n cung HM). Chøng minh t¬ng tù ta cã tø gi¸c MHBI néi tiÕp => ÐMHI = ÐMBI (néi tiÕp cïng ch¾n cung IM). Mµ ÐHCM = ÐMBI ( = 1/2 s® ) => ÐHKM = ÐMHI (1). Chøng minh t¬ng tù ta còng cã ÐKHM = ÐHIM (2). Tõ (1) vµ (2) => D HIM ~ D KHM. Theo trªn D HIM ~ D KHM => => MI.MK = MH2 Bµi 28 Cho tam gi¸c ABC néi tiÕp (O). Gäi H lµ trùc t©m cña tam gi¸c ABC; E lµ ®iÓm ®èi xøng cña H qua BC; F lµ ®iÓm ®èi xøng cña H qua trung ®iÓm I cña BC. Chøng minh tø gi¸c BHCF lµ h×nh b×nh hµnh. E, F n»m trªn ®êng trßn (O). Chøng minh tø gi¸c BCFE lµ h×nh thang c©n. Gäi G lµ giao ®iÓm cña AI vµ OH. Chøng minh G lµ träng t©m cña tam gi¸c ABC. Lêi gi¶i: 1. Theo gi¶ thiÕt F lµ ®iÓm ®èi xøng cña H qua trung ®iÓm I cña BC => I lµ trung ®iÓm BC vµ HE => BHCF lµ h×nh b×nh hµnh v× cã hai ®êng chÐo c¾t nhau t¹i trung ®iÓm cña mçi ®êng . 2. (HD) Tø gi¸c AB’HC’ néi tiÕp => ÐBAC + ÐB’HC’ = 1800 mµ ÐBHC = ÐB’HC’ (®èi ®Ønh) => ÐBAC + ÐBHC = 1800. Theo trªn BHCF lµ h×nh b×nh hµnh => ÐBHC = ÐBFC => ÐBFC + ÐBAC = 1800 => Tø gi¸c ABFC néi tiÕp => F thuéc (O). * H vµ E ®èi xøng nhau qua BC => DBHC = DBEC (c.c.c) => ÐBHC = ÐBEC => Ð BEC + ÐBAC = 1800 => ABEC néi tiÕp => E thuéc (O) . 3. Ta cã H vµ E ®èi xøng nhau qua BC => BC ^ HE (1) vµ IH = IE mµ I lµ trung ®iÓm cña cña HF => EI = 1/2 HE => tam gi¸c HEF vu«ng t¹i E hay FE ^ HE (2) Tõ (1) vµ (2) => EF // BC => BEFC lµ h×nh thang. (3) Theo trªn E Î(O) => ÐCBE = ÐCAE ( néi tiÕp cïng ch¾n cung CE) (4). Theo trªn F Î(O) vµ ÐFEA =900 => AF lµ ®êng kÝnh cña (O) => ÐACF = 900 => ÐBCF = ÐCAE ( v× cïng phô ÐACB) (5). Tõ (4) vµ (5) => ÐBCF = ÐCBE (6). Tõ (3) vµ (6) => tø gi¸c BEFC lµ h×nh thang c©n. 4. Theo trªn AF lµ ®êng kÝnh cña (O) => O lµ trung ®iÓm cña AF; BHCF lµ h×nh b×nh hµnh => I lµ trung ®iÓm cña HF => OI lµ ®êng trung b×nh cña tam gi¸c AHF => OI = 1/ 2 AH. Theo gi¶ thiÕt I lµ trung ®iÓm cña BC => OI ^ BC ( Quan hÖ ®êng kÝnh vµ d©y cung) => ÐOIG = ÐHAG (v× so le trong); l¹i cã ÐOGI = Ð HGA (®èi ®Ønh) => DOGI ~ DHGA => mµ OI = AH => mµ AI lµ trung tuyÕn cña tam gi¸c ABC (do I lµ trung ®iÓm cña BC) => G lµ träng t©m cña tam gi¸c ABC. Bµi 29 BC lµ mét d©y cung cña ®êng trßn (O; R) (BC 2R). §iÓm A di ®éng trªn cung lín BC sao cho O lu«n n»m trong tam gi¸c ABC. C¸c ®êng cao AD, BE, CF cña tam gi¸c ABC ®ång quy t¹i H. Chøng minh tam gi¸c AEF ®ång d¹ng víi tam gi¸c ABC. Gäi A’ lµ trung ®iÓm cña BC, Chøng minh AH = 2OA’. Gäi A1 lµ trung ®iÓm cña EF, Chøng minh R.AA1 = AA’. OA’. Chøng minh R(EF + FD + DE) = 2SABC suy ra vÞ trÝ cña A ®Ó tæng EF + FD + DE ®¹t gi¸ trÞ lín nhÊt. Lêi gi¶i: (HD) 1. Tø gi¸c BFEC néi tiÕp => ÐAEF = ÐACB (cïng bï ÐBFE) ÐAEF = ÐABC (cïng bï ÐCEF) => D AEF ~ D ABC. 2. VÏ ®êng kÝnh AK => KB // CH ( cïng vu«ng gãc AB); KC // BH (cïng vu«ng gãc AC) => BHKC lµ h×nh b×nh hµnh => A’ lµ trung ®iÓm cña HK => OK lµ ®êng trung b×nh cña DAHK => AH = 2OA’ 3. ¸p dông tÝnh chÊt : nÕu hai tam gi¸c ®ång d¹ng th× tØ sè gi÷a hia trung tuyÕn, tØ sè gi÷a hai b¸n kÝnh c¸c ®êng trßn ngo¹i tiÕp b»ng tØ sè ®ång d¹ng. ta cã : D AEF ~ D ABC => (1) trong ®ã R lµ b¸n kÝnh ®êng trßn ngo¹i tiÕp DABC; R’ lµ b¸n kÝnh ®êng trßn ngo¹i tiÕp D AEF; AA’ lµ trung tuyÕn cña DABC; AA1 lµ trung tuyÕn cña DAEF. Tø gi¸c AEHF néi tiÕp ®êng trßn ®êng kÝnh AH nªn ®©y còng lµ ®êng trßn ngo¹i tiÕp DAEF Tõ (1) => R.AA1 = AA’. R’ = AA’ = AA’ . VËy R . AA1 = AA’ . A’O (2) 4. Gäi B’, C’lÇn lît lµ trung ®iÓm cña AC, AB, ta cã OB’^AC ; OC’^AB (b¸n kÝnh ®i qua trung ®iÓm cña mét d©y kh«ng qua t©m) => OA’, OB’, OC’ lÇn lît lµ c¸c ®êng cao cña c¸c tam gi¸c OBC, OCA, OAB. SABC = SOBC+ SOCA + SOAB =( OA’ . BC’ + OB’ . AC + OC’ . AB ) 2SABC = OA’ . BC + OB’ . AC’ + OC’ . AB (3) Theo (2) => OA’ = R . mµ lµ tØ sè gi÷a 2 trung tuyÕn cña hai tam gi¸c ®ång d¹ng AEF vµ ABC nªn = . T¬ng tù ta cã : OB’ = R .; OC’ = R . Thay vµo (3) ta ®îc 2SABC = R () ó 2SABC = R(EF + FD + DE) * R(EF + FD + DE) = 2SABC mµ R kh«ng ®æi nªn (EF + FD + DE) ®¹t gÝ trÞ lín nhÊt khi SABC. Ta cã SABC = AD.BC do BC kh«ng ®æi nªn SABC lín nhÊt khi AD lín nhÊt, mµ AD lín nhÊt khi A lµ ®iÓm chÝnh giìa cña cung lín BC. Bµi 30 Cho tam gi¸c ABC néi tiÕp (O; R), tia ph©n gi¸c cña gãc BAC c¾t (O) t¹i M. VÏ ®êng cao AH vµ b¸n kÝnh OA. Chøng minh AM lµ ph©n gi¸c cña gãc OAH. Gi¶ sö ÐB > ÐC. Chøng minh ÐOAH = ÐB - ÐC. Cho ÐBAC = 600 vµ ÐOAH = 200. TÝnh: ÐB vµ ÐC cña tam gi¸c ABC. b) DiÖn tÝch h×nh viªn ph©n giíi h¹n bëi d©y BC vµ cung nhá BC theo R Lêi gi¶i: (HD) 1. AM lµ ph©n gi¸c cña ÐBAC => ÐBAM = ÐCAM => => M lµ trung ®iÓm cña cung BC => OM ^ BC; Theo gi¶ thiÕt AH ^ BC => OM // AH => ÐHAM = ÐOMA ( so le). Mµ ÐOMA = ÐOAM ( v× tam gi¸c OAM c©n t¹i O do cã OM = OA = R) => ÐHAM = OAM => AM lµ tia ph©n gi¸c cña gãc OAH. 2. VÏ d©y BD ^ OA => => ÐABD = ÐACB. Ta cã ÐOAH = Ð DBC ( gãc cã c¹nh t¬ng øng vu«ng gãc cïng nhän) => ÐOAH = ÐABC - ÐABD => ÐOAH = ÐABC - ÐACB hay ÐOAH = ÐB - ÐC. 3. a) Theo gi¶ thiÕt ÐBAC = 600 => ÐB + ÐC = 1200 ; theo trªn ÐB ÐC = ÐOAH => ÐB - ÐC = 200 . => b) Svp = SqBOC - SBOC = =
Tài liệu đính kèm:
 de_cuong_tong_hop_cac_dang_toan_thi_vao_lop_10_truong_thcs_d.doc
de_cuong_tong_hop_cac_dang_toan_thi_vao_lop_10_truong_thcs_d.doc





