Đề cương ôn tập Toán Lớp 9 - Năm học 2010-2011
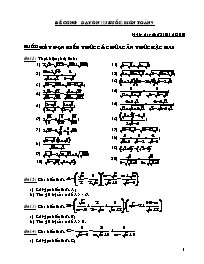
Bài 6: Cho biểu thức
a) Rút gọn biểu thức M;
b) So sánh M với 1.
Bài 7: Cho các biểu thức và
a) Rút gọn biểu thức P và Q;
b) Tìm giá trị của x để P = Q.
Bài 8: Cho biểu thức
a) Rút gọn biểu thức P
b) So sánh P với 5.
c) Với mọi giá trị của x làm P có nghĩa, chứng minh biểu thức chỉ nhận đúng một giá trị nguyên.
Bài 9: Cho biểu thức
a) Tìm điều kiện để P có nghĩa, rút gọn biểu thức P;
b) Tìm các số tự nhiên x để là số tự nhiên;
c) Tính giá trị của P với x = 4 – 2.
Bạn đang xem 20 trang mẫu của tài liệu "Đề cương ôn tập Toán Lớp 9 - Năm học 2010-2011", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Đề cương dạy ôn (15 buổi)- môn toán 9 Ngày dạy: thứ 2/10 / 5/2010 Buổi 1:rút gọn biểu thức Có chứa căn thức bậc hai Bài 1: Thực hiện phép tính: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) 9) ; 10) ; 11) ; 12) ; 13) ; 14) ; 15) ; 16) ; 17) ; 18) ; 19) 20) . Bài 2: Cho biểu thức Rút gọn biểu thức A; Tìm giá trị của x để A > - 6. Bài 3: Cho biểu thức Rút gọn biểu thức B; Tìm giá trị của x để A > 0. Bài 4: Cho biểu thức Rút gọn biểu thức C; Tìm giá trị của x để C < 1. Bài 5: Rút gọn biểu thức : a) ; b) ; c) ; d) ................................................................................................................................. Ngày dạy: thứ 3/11 / 5/2010 Buổi 2: rút gọn biểu thức Có chứa căn thức bậc hai ( Bài tập tổng hợp) Bài 6: Cho biểu thức Rút gọn biểu thức M; So sánh M với 1. Bài 7: Cho các biểu thức và Rút gọn biểu thức P và Q; Tìm giá trị của x để P = Q. Bài 8: Cho biểu thức Rút gọn biểu thức P So sánh P với 5. Với mọi giá trị của x làm P có nghĩa, chứng minh biểu thức chỉ nhận đúng một giá trị nguyên. Bài 9: Cho biểu thức Tìm điều kiện để P có nghĩa, rút gọn biểu thức P; Tìm các số tự nhiên x để là số tự nhiên; Tính giá trị của P với x = 4 – 2. Bài 10: Cho biểu thức : Rút gọn biểu thức P; Tìm x để . Buổi 3: Ôn tập phần hệ thức lượng trong tam giác vuông và góc với đường tròn. Bài 1 Cho tam giác cân ABC (AB = AC), I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp góc A, O là trung điểm của IK. Chứng minh B, C, I, K cùng nằm trên một đường tròn. Chứng minh AC là tiếp tuyến của đường tròn (O). Tính bán kính đường tròn (O) Biết AB = AC = 20 Cm, BC = 24 Cm. Lời giải: (HD) 1. Vì I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp góc A nên BI và BK là hai tia phân giác của hai góc kề bù đỉnh B Do đó BI ^ BK hayéIBK = 900 . Tương tự ta cũng có éICK = 900 như vậy B và C cùng nằm trên đường tròn đường kính IK do đó B, C, I, K cùng nằm trên một đường tròn. Ta có éC1 = éC2 (1) ( vì CI là phân giác của góc ACH. éC2 + éI1 = 900 (2) ( vì éIHC = 900 ). éI1 = é ICO (3) ( vì tam giác OIC cân tại O) Từ (1), (2) , (3) => éC1 + éICO = 900 hay AC ^ OC. Vậy AC là tiếp tuyến của đường tròn (O). Từ giả thiết AB = AC = 20 Cm, BC = 24 Cm => CH = 12 cm. AH2 = AC2 – HC2 => AH = = 16 ( cm) CH2 = AH.OH => OH = = 9 (cm) OC = = 15 (cm) Bài 2 Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì ( M khác A) kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ^ MB, BD ^ MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB. Chứng minh tứ giác AMBO nội tiếp. Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn . Chứng minh OI.OM = R2; OI. IM = IA2. Chứng minh OAHB là hình thoi. Chứng minh ba điểm O, H, M thẳng hàng. Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳngd Lời giải: (HS tự làm). Vì K là trung điểm NP nên OK ^ NP ( quan hệ đường kính Và dây cung) => éOKM = 900. Theo tính chất tiếp tuyến ta có éOAM = 900; éOBM = 900. như vậy K, A, B cùng nhìn OM dưới một góc 900 nên cùng nằm trên đường tròn đường kính OM. Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn 3. Ta có MA = MB ( t/c hai tiếp tuyến cắt nhau); OA = OB = R => OM là trung trực của AB => OM ^ AB tại I . Theo tính chất tiếp tuyến ta có éOAM = 900 nên tam giác OAM vuông tại A có AI là đường cao. áp dụng hệ thức giữa cạnh và đường cao => OI.OM = OA2 hay OI.OM = R2; và OI. IM = IA2. 4. Ta có OB ^ MB (tính chất tiếp tuyến) ; AC ^ MB (gt) => OB // AC hay OB // AH. OA ^ MA (tính chất tiếp tuyến) ; BD ^ MA (gt) => OA // BD hay OA // BH. => Tứ giác OAHB là hình bình hành; lại có OA = OB (=R) => OAHB là hình thoi. 5. Theo trên OAHB là hình thoi. => OH ^ AB; cũng theo trên OM ^ AB => O, H, M thẳng hàng( Vì qua O chỉ có một đường thẳng vuông góc với AB). 6. (HD) Theo trên OAHB là hình thoi. => AH = AO = R. Vậy khi M di động trên d thì H cũng di động nhưng luôn cách A cố định một khoảng bằng R. Do đó quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A bán kính AH = R Buổi 4: Ôn Hình tổng hợp Baứi 1: Cho (O,R) vaứ moọt ủieồm A ụỷ ngoaứi ủửụứng troứn sao cho OA = 3R. Tửứ A veừ hai tieỏp tuyeỏn AB, AC ủeỏn ủửụứng troứn (O) vụựi B, C laứ hai tieỏp ủieồm Chửựng minh: Tửự giaực OBAC laứ moọt tửự giaực noọi tieỏp. Tửứ B veừ ủửụứng thaỳng song song vụựi AC, caột ủửụứng troứn (O) taùi ủieồm D (khaực ủieồm B) ủửụứng thaỳng AD caột ủửụứng troứn (O) taùi E (khaực D). Chửựng minh: AB2 = AE. AD Chửựng minh: Tia ủoỏi cuỷa tia EC laứ tia phaõn giaực cuỷa Tớnh dieọn tớch tam giaực BDC theo R. HệễÙNG DAÃN ị OBAC laứ tửự giaực noọi tieỏp (toồng 2 goực ủoỏi baống 1800) b) Xeựt DAEB vaứ DABD, ta coự: Vaọy: DAEB ~ DABD(g-g) C) Gọi Ex là tia đối của tia EC d) D ABC vuoõng taùi B cho OA2 = OB2+ AB2( Pitago) vaứ chửựng minh ủửụùc OA ^BC taùi H ị AB2 = (3R)2- (R)2ị AB = R D ABO vuoõng coự ba caùnh laứ R, R,3R Caực tam giaực vuoõng OHC vaứ ICB cuứng ủoàng daùng vụựi tam giaực vuoõng ABO cho: Baứi 2: Cho ủửụứng troứn (O) coự baựn kớnh R vaứ moọt ủieồm S ụỷ ngoaứi ủửụứng troứn (O). Tửỷ S veừ hai tieỏp tuyeỏn SA, SB vụựi ủửụứng troứn (O)(A, B laứ hai tieỏp ủieồm). Veừ ủửụứng thaỳng a ủi qua S caột ủửụứng troứn(O) taùi hai ủieồm M, N vụựi M naốm giửừa hai ủieồm S vaứ N (ủửụứng thaỳng a khoõng ủi qua taõm O) Chửựng minh raống: SO vuoõng goực vụựi AB Goùi H laứ giao ủieồm cuỷa SO vaứ AB, goùi I laứ trung ủieồm cuỷa MN. Hai ủửụứng thaỳng OI vaứ AB caột nhau taùi ủieồm E. chửựng minh: IHSE laứ moọt tửự giaực noọi tieỏp. Chửựng minh: OI.OE = R2 Cho bieỏt SO = 2R vaứ MN = R . Tớnh dieọn tớch tam giaực ESM theo R HệễÙNG DAÃN a) Chửựng minh: SO^ AB Ta coự: SA = SB (2 tt caột nhau) Suy ra DSAB caõn taùi S. ta coự SO laứ tia phaõn giaực cuỷa neõn cuừng laứ ủửụứng cao cuỷa tam giaực SAB. Neõn SO^ AB Caựch khaực: SA = SB OA= OB Neõn SO laứ trung trửùc cuỷa AB. Suy ra: SO^ AB b) Chửng minh: IHSE laứ moọt tửự giaực noọi tieỏp Ta coự: Neõn : (cuứng nhỡn SE dửụựi goực 900) Vaọy tửự giaực IHSE noọi tieỏp ủửụùc ủửụứng troứn. c) Chửựng minh: OI.OE = R2 Xeựt DOIH vaứ DOSE, ta coự: laứ goực chung ( tửự giaực IHSE n/tieỏp) Vaọy: DOIH ~ DOSE(g-g) Maứ OH.OS = OA2 = R2(heọ thửực lửụùng trong DAOS) Vaọy: OI.OE = R2. d) Tớnh dieọn tớch tam giaực ESM theo R. Ta coự : OI = R/2 ( vỡ MN laứ caùnh cuỷa tam giaực ủeàu noọi tieỏp(O,R)) Maứ: OI.OE = R2. Neõn OE = 2R Ta coự: IE = OE – OI = 2R – R/2= 3R/2 Tam giaực vuoõng OIS cho: Ngày dạy : Buổi 5: ÔN Hệ phương trình Baứi 1: : Giải các HPT sau: 1.1. a. b. Giải: a. Dùng PP thế: Vaọy HPT đã cho có nghiệm là: Dùng PP cộng: Vaọy HPT đã cho có nghiệm là: Để giảI loại HPT này ta thường sử dụng PP cộng cho thuận lợi. Vaọy HPT có nghiệm là Đối với HPT ở dạng này ta có thể sử dụng hai cách giảI sau đây: 1.2. + Cách 1: Sử dụng PP cộng. ĐK: . Vaọy HPT có nghiệm là + Cách 2: Sử dụng PP đặt ẩn phụ. ĐK: . Đặt ; . HPT đã cho trở thành: (TMĐK) Vaọy HPT có nghiệm là Lưu ý: - Nhiều em còn thiếu ĐK cho những HPT ở dạng này. - Có thể thử lại nghiệm của HPT vừa giải. Baứi 2: Giaỷi caực heọ phửụng trỡnh sau (baống pp theỏ) 1.1: 1.2. Baứi 3: Giaỷi caực heọ phửụng trỡnh sau (baống pp coọng ủaùi soỏ) 2.1. 2.2. Baứi 4: Giaỷi heọ phửụng trỡnh trong moói trửụứng hụùp sau a) m = -1 b) m = 0 c) m = 1 Baứi 5: a) Xaực ủũnh heọ soỏ avaứb, bieỏt raống heọ phửụng trỡnhcoự nghieọm laứ (1; -2) b) Cuừng hoỷi nhử vaọy neỏu heọ phửụng trỡnh coự nghieọm Baứi 6: Giaỷi heọ phửụng trỡnh sau: Tửứ ủoự suy ra nghieọm cuỷa heọ phửụng trỡnh Baứi 7: Giaỷi caực heọ phửụng trỡnh sau: ; ; ; ; ; ; ; ; ; Bài 8: Cho hệ phương trình Giải hệ khi a=3 ; b=-2 Tìm a;b để hệ có nghiệm là (x;y)=( Bài 9: GiảI các hệ phương trình sau a) b) c) (đk x;y2 ) ; ; ; ; ; ; . ; ; ; ; ; ........................................................................................................................... Ngày dạy: Buổi 6: Ôn hình tổng hợp( Tiếp) Baứi 1: Cho r ABC coự ba goực nhoùn noọi tieỏp trong ủửụứng troứn (O,R) vaứ coự 3 ủửụứng cao AD , BE , CF caột nhau taùi H . a) CMR: caực tửự giaực BFEC, AFHE laứ caực tửự giaực noọi tieỏp ủửụùc . b) CMR: Tia DA laứ tia phaõn giaực cuỷa goực EDF. c) ẹửụứng thaỳng AO caột ủửụứng troứn (O) taùi ủieồm K (khaực ủieồm A). CMR: Tửự giaực BHCK laứ moọt hỡnh bỡnh haứnh. d)Goùi G laứ troùng taõm cuỷa r ABC. CMR : HệễÙNG DAÃN a) Chửựng minh: tửự giaực BFEC, AFHE laứ caực tửự giaực noọi tieỏp ủửụùc. Trong tửự giaực BFEC, ta coự: Vaọy: tửự giaực BFEC noọi tieỏp. Trong tửự giaực AFHE, ta coự: Vaọy: AFHE noọi tieỏp ủửụùc ( toồng 2 goực ủoỏi dieọn baống 1800) b) CMR: Tia DA laứ tia phaõn giaực cuỷa goực EDF. Trong BFHD, ta coự: Vaọy: BFHDnoọi tieỏp ủửụùc ( toồng 2 goực ủoỏi dieọn baống 1800) Trong ABDE, ta coự: Vaọy: ABDE noọi tieỏp ủửụùc Vaọy: Tia DA laứ tia phaõn giaực cuỷa c) CMR: Tửự giaực BHCK laứ moọt hỡnh bỡnh haứnh d) CMR : Ta coự: BHCK laứ hỡnh bỡnh haứnh (cmt) hai ủửụứng cheựo HK, BC caột nhau taùi trung ủieồm M cuỷa moói ủửụứng. OM laứ trung bỡnh cuỷa DAHK. Trong DAHK, ta coự: AM vaứ OH laứ trung tuyeỏn gaởp nhau taùi troùng taõm G’. ị Maứ: G laứ troùng taõm cuứa DABC. ị Do ủoự: G’º G ị Gẻ OH Vaọy: H, G, O thaỳng haứng ị G laứ troùng taõm DAHK ị HG = 2 OG (t/c troùng taõm) Maứ: ị Baứi 2: Cho r ABC coự ba goực nhoùn noọi tieỏp trong ủửụứng troứn (O,R) vaứ coự 2 ủửụứng cao BE vaứ CF caột nhau taùi H . a) CMR: tửự giaực BFEC laứ caực tửự giaực noọi tieỏp ủửụùc . b) Hai ủửụứng thaỳng BE vaứ CF caột ủửụứng troứn (O) laàn lửụùt taùi P vaứ Q . CMR : , suy ra : EF // PQ c) CMR: OA ^ EF d) Cho BC = R. Tớnh baựn kớnh ủửụứng troứn ngoaùi tieỏp r AEF theo R HệễÙNG DAÃN CMR: tửự giaực BFEC laứ caực tửự giaực noọi tieỏp ủửụùc . Trong tửự giaực BFEC, ta coự: Vaọy: tửự giaực BFEC noọi tieỏp ủửụùc. b) CMR : , suy ra : EF // PQ Maứ: 2 goực naứy ụỷ vũ trớ ủoàng vũ ị EF// QP. c) CMR: OA ^ EF Maứ: laứ goực n/tieỏp chaộn laứ goực n/tieỏp chaộn ị = ị AQ = AP (= R) ị OA laứ trung trửùc cuỷa QP. ị OA ^ PQ Maứ : EF // PQ(cmt) OA ^ EF d) Tớnh baựn kớnh ủửụứng troứn ngoaùi tieỏp r AEF theo R Goùi I laứ trung ủieồm cuỷa AH. Trong tửự giaực AFHE, ta coự: Vaọy: tửự giaực AFHE noọi tieỏp ủửụùc.(toồng hai goực baống 1800) ị IA = IP = IE = IH = AH/2 Vaọy: I laứ taõm (AEF), baựn kớnh laứ AH/2 Keỷ ủửụứng kớnh AK; goùi H laứ giao ủieồm BE, CF. Goùi N laứ trung ủieồm BC. ị ON^ BC(ủớnh lyự ủ/ kớnh vaứ daõy cung) Ta coự: ị BH // CK (cuứng ^ AC ... ường kính CD trên tia đối của CD lấy điểm S. Nối SA cắt đường tròn tại M (M khác A). Nối MB cắt CD tại K, MC cắt AD tại H. a, Chứng minh tứ giác DKHM nội tiếp một đường tròn. b, Chứng minh HK song song với AB. c, Chứng minh CK.CD = CH.CM Bài 4:(1,5 điểm) Cho đường thẳng d: y = ax + b và (P): y = kx2 a, Tìm a và b để đường thẳng d đi qua 2 điểm A(2;3) ; B(3;9). b, Tìm k (k khác không) sao cho (P) tiếp xúc với đường thẳng d. Bài 5:(1,0 điểm) Cho x và y là 2 số thỏa mãn: Tính B = x2 + y2. ------------------------------- Hết ------------------------------- Đáp án tuyển sinh 10 Hướng dẫn chấm và thang điểm Đề thi tuyển sinh vào 10 Năm học: 2007-2008 Môn : Toán Bài Nội dung Thang điểm B1 (2đ) 1a (1đ) 1b (1đ) 1a. 1b. Đặt suy ra t2 - t - 12 = 0 Tính t1 = -3 (loại); t2 = 4 . Kết luận nghiệm x = 16 0.5 đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ B2 (2đ) 2a (1đ) 2b (1đ) 2a. Với m = 2 thay vào được x2 - 2x - 3 = 0 có dạng a - b + c = 0 ( Hoặc tính ) x1 = -1 ; x2 = 3 và kết luận nghiệm 2b. Tính Suy ra m < 4 và kết luận m < 4 phương trình có nghiệm 0.25đ 0.25đ 0.5 đ 0.5 đ 0.25đ 0.25đ B3 (3,5đ) 3a (1,5đ) 3b (1đ) 3c (1đ) 3a. Vẽ hình đúng (Chú ý không vẽ hình không chấm điểm) Ta có chắn cung CB chẵn cung CA mà cung CA = cung CB Từ đó Suy ra tứ giác DKHM nội tiếp một đường tròn 3b. Ta có ( tứ giác DMHK nội tiếp) ( tứ giác ABDM nội tiếp) Từ đó suy ra Vậy ta có HK song song với AB 3c. Chứng minh đồng dạng . Thật vậy ta có Xét và có góc C chung ( tứ giác DMHK nội tiếp) Từ đó ta có Đpcm. 0.5 đ 0.5 đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.5 đ B4 (1,5đ) 4a (1đ) 4b (0.5đ) 4a. Đi qua điểm A(2;3) thay x = 2 và y = 3 3 = 2a + b (1) Đi qua điểm B(3;9) thay x = 3 và y = 9 9 = 3a + b (2) Kết hợp (1) và (2) ta được hệ Kết luận đường thẳngd: y = 6x - 9 4b. Suy ra kx2 = 6x - 9 có nghiệm kép Suy ra k = 1 và kết luận 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ 0.25đ B5 (1 đ) Từ x3 + 2y2 - 4y + 3 = 0 x3 = -1 - 2(y - 1)2 -1(1) Từ x2 + x2y2 - 2y = 0 (2) Kết hợp (1) và (2) suy ra x = -1 do đó y = 1 Vậy B = x2 + y2 = 2 0.25đ 0.25đ 0.25đ 0.25đ Chú ý: Học sinh làm theo cách khác nếu đúng vẫn cho điểm tối đa. ------------------------------------ Hết ------------------------------------ Buổi 14: Đề 2 Câu1 : Cho biểu thức A=Với xạ;±1 .a, Ruý gọn biểu thức A .b , Tính giá trị của biểu thức khi cho x= c. Tìm giá trị của x để A=3 Câu2.a, Giải hệ phương trình: b. Giải bất phương trình: <0 Câu3. Cho phương trình (2m-1)x2-2mx+1=0 Xác định m để phương trình trên có nghiệm thuộc khoảng (-1,0) Câu 4. Cho nửa đường tròn tâm O , đường kính BC .Điểm A thuộc nửa đường tròn đó Dưng hình vuông ABCD thuộc nửa mặt phẳng bờ AB, không chứa đỉnh C. Gọi Flà giao điểm của Aevà nửa đường tròn (O) . Gọi Klà giao điểm của CFvà ED chứng minh rằng 4 điểm E,B,F,K. nằm trên một đường tròn Tam giác BKC là tam giác gì ? Vì sao. ? đáp án Câu 1: a. Rút gọn A= b.Thay x= vào A ta được A= c.A=3 x2-3x-2=0=> x= Câu 2 : a)Đặt x-y=a ta được pt: a2+3a=4 => a=-1;a=-4 Từ đó ta có * (1) *(2) Giải hệ (1) ta được x=3, y=2 Giải hệ (2) ta được x=0, y=4 Vậy hệ phương trình có nghiệm là x=3, y=2 hoặc x=0; y=4 Ta có x3-4x2-2x-15=(x-5)(x2+x+3) mà x2+x+3=(x+1/2)2+11/4>0 với mọi x Vậy bất phương trình tương đương với x-5>0 =>x>5 Câu 3: Phương trình: ( 2m-1)x2-2mx+1=0 Xét 2m-1=0=> m=1/2 pt trở thành –x+1=0=> x=1 Xét 2m-1ạ0=> mạ 1/2 khi đó ta có = m2-2m+1= (m-1)2³0 mọi m=> pt có nghiệm với mọi m ta thấy nghiệm x=1 không thuộc (-1,0) với mạ 1/2 pt còn có nghiệm x== pt có nghiệm trong khoảng (-1,0)=> -1<<0 =>=>m<0 Vậy Pt có nghiệm trong khoảng (-1,0) khi và chỉ khi m<0 Câu 4: a. Ta có KEB= 900 mặt khác BFC= 900( góc nội tiếp chắn nữa đường tròn) do CF kéo dài cắt ED tại D => BFK= 900 => E,F thuộc đường tròn đường kính BK hay 4 điểm E,F,B,K thuộc đường tròn đường kính BK. b. BCF= BAF Mà BAF= BAE=450=> BCF= 450 Ta có BKF= BEF Mà BEF= BEA=450(EA là đường chéo của hình vuông ABED)=> BKF=450 Vì BKC= BCK= 450=> tam giác BCK vuông cân tại B Buổi 15 : Đề 3 Bài 1: Cho biểu thức: P = a,Rút gọn P b,Tìm x nguyên để P có giá trị nguyên. Bài 2: Cho phương trình: x2-( 2m + 1)x + m2 + m - 6= 0 (*) a.Tìm m để phương trình (*) có 2 nghiệm âm. b.Tìm m để phương trình (*) có 2 nghiệm x1; x2 thoả mãn =50 Bài 3: Cho phương trình: ax2 + bx + c = 0 có hai nghiệm dương phân biệt x1, x2Chứng minh: a,Phương trình ct2 + bt + a =0 cũng có hai nghiệm dương phân biệt t1 và t2. b,Chứng minh: x1 + x2 + t1 + t2 4 Bài 4: Cho tam giác có các góc nhọn ABC nội tiếp đường tròn tâm O . H là trực tâm của tam giác. D là một điểm trên cung BC không chứa điểm A. a, Xác định vị trí của điẻm D để tứ giác BHCD là hình bình hành. b, Gọi P và Q lần lượt là các điểm đối xứng của điểm D qua các đường thẳng AB và AC . Chứng minh rằng 3 điểm P; H; Q thẳng hàng. c, Tìm vị trí của điểm D để PQ có độ dài lớn nhất. Bài 5: Cho hai số dương x; y thoả mãn: x + y 1 Tìm giá trị nhỏ nhất của: A = Đáp án Bài 1: (2 điểm). ĐK: x a, Rút gọn: P = P = b. P = Để P nguyên thì Vậy với x= thì P có giá trị nguyên. Bài 2: Để phương trình có hai nghiệm âm thì: b. Giải phương trình: Bài 3: a. Vì x1 là nghiệm của phương trình: ax2 + bx + c = 0 nên ax12 + bx1 + c =0. . Vì x1> 0 => c. Chứng tỏ là một nghiệm dương của phương trình: ct2 + bt + a = 0; t1 = Vì x2 là nghiệm của phương trình: ax2 + bx + c = 0 => ax22 + bx2 + c =0 vì x2> 0 nên c. điều này chứng tỏ là một nghiệm dương của phương trình ct2 + bt + a = 0 ; t2 = Vậy nếu phương trình: ax2 + bx + c =0 có hai nghiẹm dương phân biệt x1; x2 thì phương trình : ct2 + bt + a =0 cũng có hai nghiệm dương phân biệt t1 ; t2 . t1 = ; t2 = b. Do x1; x1; t1; t2 đều là những nghiệm dương nên t1+ x1 = + x1 2 t2 + x2 = + x2 2 Do đó x1 + x2 + t1 + t2 4 Bài 4 a. Giả sử đã tìm được điểm D trên cung BC sao cho tứ giác BHCD là hình bình hành . Khi đó: BD//HC; CD//HB vì H là trực tâm tam giác ABC nên CH và BH => BD và CD. Do đó: ABD = 900 và ACD = 900 . Vậy AD là đường kính của đường tròn tâm O Ngược lại nếu D là đầu đường kính AD của đường tròn tâm O thì tứ giác BHCD là hình bình hành. Vì P đối xứng với D qua AB nên APB = ADB nhưng ADB =ACB nhưng ADB = ACB Do đó: APB = ACB Mặt khác: AHB + ACB = 1800 => APB + AHB = 1800 Tứ giác APBH nội tiếp được đường tròn nên PAB = PHB Mà PAB = DAB do đó: PHB = DAB Chứng minh tương tự ta có: CHQ = DAC Vậy PHQ = PHB + BHC + CHQ = BAC + BHC = 1800 Ba điểm P; H; Q thẳng hàng c). Ta thấy APQ là tam giác cân đỉnh A Có AP = AQ = AD và PAQ = 2BAC không đổi nên cạnh đáy PQ đạt giá trị lớn nhất ú AP và AQ là lớn nhất hay ú AD là lớn nhất ú D là đầu đường kính kẻ từ A của đường tròn tâm O . ........................................................................................................ Tham khảo một số đề sau tuỳ đối tượng HS Đề 1: Câu 1: Cho hàm số f(x) = a) Tính f(-1); f(5) b) Tìm x để f(x) = 10 c) Rút gọn A = khi x ạ Câu 2: Giải hệ phương trình Câu 3: Cho biểu thứcA = với x > 0 và x ạ 1 a) Rút gọn A b) Tìm giá trị của x để A = 3 Câu 4: Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA; PB. Gọi H là chân đường vuông góc hạ từ A đến đường kính BC. a) Chứng minh rằng PC cắt AH tại trung điểm E của AH b) Giả sử PO = d. Tính AH theo R và d. Câu 5: Cho phương trình 2x2 + (2m - 1)x + m - 1 = 0 Không giải phương trình, tìm m để phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn: 3x1 - 4x2 = 11 đáp án Câu 1a) f(x) = Suy ra f(-1) = 3; f(5) = 3 b) c) Với x > 2 suy ra x - 2 > 0 suy ra Với x < 2 suy ra x - 2 < 0 suy ra Câu 2 Câu 3 a) Ta có: A = = = = = = = b) A = 3 => = 3 => 3x + - 2 = 0 => x = 2/3 Câu 4 O B C H E A P Do HA // PB (Cùng vuông góc với BC) nên theo định lý Ta let áp dụng cho CPB ta có ; (1) Mặt khác, do PO // AC (cùng vuông góc với AB) => POB = ACB (hai góc đồng vị) => D AHC D POB Do đó: (2) Do CB = 2OB, kết hợp (1) và (2) ta suy ra AH = 2EH hay E là trung điểm của AH. b) Xét tam giác vuông BAC, đường cao AH ta có AH2 = BH.CH = (2R - CH).CH Theo (1) và do AH = 2EH ta có AH2.4PB2 = (4R.PB - AH.CB).AH.CB 4AH.PB2 = 4R.PB.CB - AH.CB2 AH (4PB2 +CB2) = 4R.PB.CB Câu 5 Để phương trình có 2 nghiệm phân biệt x1 ; x2 thì D > 0 (2m - 1)2 - 4. 2. (m - 1) > 0 Từ đó suy ra m ạ 1,5 (1) Mặt khác, theo định lý Viét và giả thiết ta có: Giải phương trình ta được m = - 2 và m = 4,125 (2) Đối chiếu điều kiện (1) và (2) ta có: Với m = - 2 hoặc m = 4,125 thì phương trình đã cho có hai nghiệm phân biệt thỏa mãn: x1 + x2 = 11 Đề 2: Câu 1: Cho P = + - a/. Rút gọn P. b/. Chứng minh: P < với x 0 và x 1. Câu 2: Cho phương trình : x2 – 2(m - 1)x + m2 – 3 = 0 ( 1 ) ; m là tham số. a/. Tìm m để phương trình (1) có nghiệm. b/. Tìm m để phương trình (1) có hai nghiệm sao cho nghiệm này bằng ba lần nghiệm kia. Câu 3: a/. Giải phương trình : + = 2 b/. Cho a, b, c là các số thực thõa mãn : Tìm giá trị lớn nhất và giá trị bé nhất của Q = 6 a + 7 b + 2006 c. Câu 4: Cho cân tại A với AB > BC. Điểm D di động trên cạnh AB, ( D không trùng với A, B). Gọi (O) là đường tròn ngoại tiếp . Tiếp tuyến của (O) tại C và D cắt nhau ở K . a/. Chứng minh tứ giác ADCK nội tiếp. b/. Tứ giác ABCK là hình gì? Vì sao? c/. Xác định vị trí điểm D sao cho tứ giác ABCK là hình bình hành. Đáp án Câu 1: Điều kiện: x 0 và x 1. (0,25 điểm) P = + - = + - = = = b/. Với x 0 và x 1 .Ta có: P < < 3 0 ) x - 2 + 1 > 0 ( - 1)2 > 0. ( Đúng vì x 0 và x 1) Câu 2:a/. Phương trình (1) có nghiệm khi và chỉ khi ’ 0. (m - 1)2 – m2 – 3 0 4 – 2m 0 m 2. b/. Với m 2 thì (1) có 2 nghiệm. Gọi một nghiệm của (1) là a thì nghiệm kia là 3a . Theo Viet ,ta có: a= 3()2 = m2 – 3 m2 + 6m – 15 = 0 m = –32 ( thõa mãn điều kiện). Câu 3: Điều kiện x 0 ; 2 – x2 > 0 x 0 ; < . Đặt y = > 0 Ta có: Từ (2) có : x + y = 2xy. Thay vào (1) có : xy = 1 hoặc xy = - * Nếu xy = 1 thì x+ y = 2. Khi đó x, y là nghiệm của phương trình: X2 – 2X + 1 = 0 X = 1 x = y = 1. * Nếu xy = - thì x+ y = -1. Khi đó x, y là nghiệm của phương trình: X2 + X - = 0 X = Vì y > 0 nên: y = x = Vậy phương trình có hai nghiệm: x1 = 1 ; x2 = Câu 4: c/. Theo câu b, tứ giác ABCK là hình thang. Do đó, tứ giác ABCK là hình bình hành AB // CK Mà sđ = sđ = Nên Dựng tia Cy sao cho .Khi đó, D là giao điểm của và Cy. Với giả thiết > thì > > . D AB . Vậy điểm D xác định như trên là điểm cần tìm.
Tài liệu đính kèm:
 giao an on thi toan 9.doc
giao an on thi toan 9.doc





