Bồi dưỡng học sinh giỏi Toán Lớp 8 - Tạ Phạm Hải
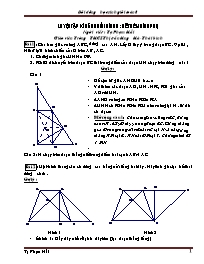
Cho tam giác vuông ABC , đờng cao AH . Lấy D tùy ý trong đoạn BC . Gọi M , N thứ tự là hình chiếu của D trên AB , AC .
1. Chứng minh góc MHN = 900.
2. Khi D di chuyển trên đoạn BC thì trung điểm của đoạn MN chạy trên đờng nào ?
Gợi ý :
Câu 1
- Dễ c/m tứ giác ANDM là h.c. n
- Vẽ thêm các đoạn AD , MN . HK , K là giao của AD với MN.
- ∆AHD vuông ? KH = KD = KA
- ∆MHN có KH = KN = KM nên vuông tại H . từ đó có đpcm
- Mở rộng câu 1: Cho tam giác vuông ABC , đờng cao AH . Lấy D tùy ý trong đoạn BC .Đờng thẳng qua D song song với AB cắt AC tại N và cắt đờng thẳng HM tại E . HN cắt DM tại I . Chứng minh EI ? MN
Bạn đang xem tài liệu "Bồi dưỡng học sinh giỏi Toán Lớp 8 - Tạ Phạm Hải", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
luyện tập kĩ năng giải hình 8 : Vẽ thêm hình phụ Người viết : Tạ Phạm Hải Giáo viên Trường THCS Thị trấn Hưng Hà - Thái bình Bài 1 : Cho tam giác vuông ABC , đường cao AH . Lấy D tùy ý trong đoạn BC . Gọi M , N thứ tự là hình chiếu của D trên AB , AC . Chứng minh góc MHN = 900. Khi D di chuyển trên đoạn BC thì trung điểm của đoạn MN chạy trên đường nào ? Gợi ý : Câu 1 Dễ c/m tứ giác ANDM là h.c. n Vẽ thêm các đoạn AD , MN . HK , K là giao của AD với MN. ∆AHD vuông ị KH = KD = KA ∆MHN có KH = KN = KM nên vuông tại H . từ đó có đpcm Mở rộng câu 1: Cho tam giác vuông ABC , đường cao AH . Lấy D tùy ý trong đoạn BC .Đường thẳng qua D song song với AB cắt AC tại N và cắt đường thẳng HM tại E . HN cắt DM tại I . Chứng minh EI ^ MN Câu 2 : H chạy trên đoạn thẳng nối trung điểm hai cạnh AB và AC Bài 2 : Một hình thang cân có đường cao bằng nửa tổng hai đáy. Hãy tính góc tạo bởi hai đường chéo . Gợi ý : Hình 1 Hình 2 ở hình 1 : Đẩy đáy nhỏ về phía đáy lớn ( tạo đoạn thẳng tổng ) ở hình 2 : Đẩy đáy lớn về phía đáy nhỏ . Bài 3 : Tứ giác ABCD có = 1800 , CB = CD . Chứng minh AC là phân giác của Gợi ý : Hình 1 Hình 2 Hình 1 : Lấy DE = AB ị ∆CBA = ∆CDE ị ∆ACE cân tại C ... Hình 2 : Lấy BE = AD ị ∆CBE = ∆CDA ị ∆ACE cân tại C ... Bài 4 : Cho ∆ABC cân tại A . Trên cạnh AB , AC thứ tự lấy các điểm D , E sao cho BD = AE . Gọi I là trung điểm của DE . Tia AI cắt BC tại K . Chứng minh tứ giác ADKE là hình bình hành . Gợi ý : Qua E kẻ EF // BC , F ∈ AB ị ∆AEF cân tại A , nên AE = AF = BD . Gọi M là trung điểm của DF thì IM là đường trung bình của ∆DEF ị IM // BC Lại có AF + FM = BD + DM = AB / 2 vậy M cũng là trung điểm của AB và IM // BK nên IM là đường trung bình của ∆ABK , vậy IA = IK Từ đó tứ giác ADKE là h.b.h Bài 5 : Cho điểm E thuộc cạnh AC của tam giác đều ABC. Đường thẳng vuông góc với AB kẻ từ E cắt đường thẳng vuông góc với BC kẻ từ C tại D. Gọi K là trung điểm của AE, Tính góc KBD . Gợi ý : Gọi I là điểm đối xứng với D qua điểm K thì tứ giác AIED là h.b.h ị AI // DE và AI = DE ị AI ^ AB . Mặt khác dễ ch/m ∆EDC cân tại D nên DE = DC = IA vì vậy suy được ∆AIB = ∆CDB ( cgv – cgv ) ị BI = BD . ∆DBI cân tại B có BK là trung tuyến nên cũng là đường cao . Vậy góc KBD = 900 Bài 6 : Cho tam giác ABC đều , vẽ một đường thẳng song song với BC và cắt các cạnh AB , AC thứ tự ở D và E . Gọi I là trung điểm của đoạn thẳng DC , G là trọng tâm của ∆ADE , H là điểm đối xứng của B qua I . Chứng minh ∆DGB = ∆EGH Tính các góc của ∆BGI Gợi ý : 1.C/m ∆DGB = ∆EGH : Ta có DG = EG ; góc GDB = góc GEH = 1200 , BD = CH = EH 2.Từ câu 1 suy ra GB = GH hay ∆BGH cân tại G có GI là trung tuyến nên cũng là đường cao nên ∆BGI vuông tại I . Lại từ câu 1 thì góc DGB = góc EGH nên góc BGH = góc DGE = 1200 . từ đó góc BGI = 600 và góc GBI = 300 Bài 7 : Cho tam giác vuông ABC , AB < AC , đường cao AH . Trên tia HC lấy điểm D sao cho HD = HA . Đường vuông góc với BC kẻ từ D cắt AC ở E . Gọi M là trung điểm của BE , tính góc AHM Chứng minh AB = AE Gợi ý : 1.Từ đề bài suy ra MD = MA = ME = MB , từ đó đường thẳng HM là đường trung trực của đoạn thẳng AD , từ đó HM là phân giác của góc vuông AHD , vậy góc AHM = 450 2.Vì ∆BMD cân tại M nên góc MBD = MDB = MAH ( kết hợp với câu 1) . Xét hai tam giác ∆AMK và ∆BHK có góc B1 = góc A1 ( cmt) ; K1 = K2 ( đ đ) nên góc AMB = góc AHB vậy góc AMB = 900 , ị ∆ABE vuông cân , vậy AB = AE đpcm Cách 2 : Gọi F là hình chiếu của E trên AH ta có EF = HD = AH ị ∆VAEF = ∆VBAH ... Bài 8 : Cho hình thang vuông ABCD có AB // CD ; góc A = góc D = 900 ; CD = 2.AB = 2.AD . Qua điểm E thuộc cạnh AB kẻ đường vuông góc với DE , cắt BC tại F . Chứng minh tam giác DEF vuông cân . Gợi ý : Tứ giác ABCK là h.b.h ị OI // BF nên IO là đường trung bình của ∆DBF ị I là trung điểm của DF. Từ đó ∆DEF vuông cân . Bài 9 : Cho ∆ABC , trên các cạnh AC , AB thứ tự lấy các điểm E , F . Gọi H là giao điểm của BE và CF , Tia AH cắt BC ở D . Gọi trung điểm của các cạnh AB , BC , AC thứ tự là M , S , Q ; Trung điểm của các đoạn thẳng HA , HB , HC thứ tự là R , N , P. Chứng minh MP , NQ , RS đồng quy Các điểm E và F cần có thêm điều kiện gì để MP = NQ = RS ? Gợi ý : 1.Vẽ đường phụ tạo h.b.h MNPQ và gọi O là giao hai đường chéo của nó nên O là trung điểm của MP Vẽ đường phụ tạo h.b.h MRPS nên đường chéo RS của h.b.h này đi qua trung điểm của MP . Từ đó có đpcm 2.Để MP = NQ thì h.b.h MNPQ phải là h.c.n ị AH ^ BC . Để MP = RS thì h.b.h MRPS phải là h.c.n ị BH ^ AC ị H phải là trực tâm của ∆ABC ị ... Bài tập luyện tập Bài 1 : Cho ∆ABC có góc B = 450 , góc C = 1200 . trên tia BC lấy điểm D sao cho CD = 2.CB . Tính góc ADB . Bài 2 : Cho ∆ABC cân tại B và góc ABC = 800. Lấy điểm I trong tam giác sao cho góc IAC = 100 và góc ICA = 300 . Tính góc AIB ? Bài 3 : Cho ∆ABC cân tại A và có góc A = 200. từ B và C kẻ các đường thẳng BD và CE cắt các cạnh đối diện tại D , E sao cho góc CBD = 600 và góc BCE = 500. Tính góc BDE ? Bài 4 : Cho ∆ABC , trong tam giác lấy điểm P sao cho góc PBA = góc PCA . Gọi D , E thứ tự là hình chiếu của P trên AB , AC. Gọi M , H , N thứ tự là trung điểm của các đoạn thẳng PB , BC , PC . Chứng minh ∆HDE cân Bài 5 : Độ dài đường trung bình của một hình thang là 40 cm ; Hai góc kề đáy nhỏ ( góc trong ) của hình thang bằng 1300 và 1400. Hãy tìm độ dài của mỗi đáy hình thang biết rằng độ dài của đoạn thẳng nối trung điểm của hai đáy hình thang bằng 1 cm . Bài 6 : Trên cạnh Oy của góc nhọn xOy lấy hai điểm A , B sao cho A nằm giữa O và B .Trên cạnh Oy của góc này cũng lấy hai điểm C , D sao cho C nằm giữa O và D ; Cho biết AB = CD ; gọi M , N thứ tự là trung điểm của các đoạn thẳng AC , BD ; vẽ tia phân giác Oz của góc xOy . Chứng minh MN // Oz Bài 1: Cho hình vuông ABCD , lấy điểm M tùy ý trên đường chéo BD . Gọi P , Q thứ tự là hình chiếu của M trên AB , AD ; BQ cắt PD tại O . Chứng minh PC ^ BQ và CQ ^ PD Chứng minh CM ^ PQ Tìm vị trí của M trên đường chéo BD để ∆CPQ có diện tích lớn nhất
Tài liệu đính kèm:
 boi_duong_hoc_sinh_gioi_toan_lop_8_ta_pham_hai.doc
boi_duong_hoc_sinh_gioi_toan_lop_8_ta_pham_hai.doc





