Bồi dưỡng học sinh giỏi Toán Lớp 8 - Chuyên đề: Phương pháp diện tích - Tạ Phạm Hải
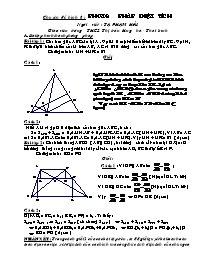
Nối AM và gọi S là diện tích của tam giác ABC , ta có :
S = SABM + SACM = 0,5.MH.AB + 0,5.MK.AC = 0,5.AC.( MH + MK ), Vì AB = AC
mà S = 0,5 BI.AC nên 0,5 BI.AC = 0,5.AC.( MH + MK ). Vậy MH + MK = BI ( đpcm )
Bài tập 2 : Cho hình thang ABCD ( AB // CD ) , hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với hai đáy cắt các cạnh bên AD , BC thứ tự ở E và F.
Chứng minh : EO = FO
Giải :
Cách 1 : Vì OF // AB nên ;
Vì OE // AB nên ( Hệ quả ĐL Ta lét )
Vì OE // DC nên (Hệ quả ĐL Ta lét )
Vậy OF = OE ( đpcm
Bạn đang xem tài liệu "Bồi dưỡng học sinh giỏi Toán Lớp 8 - Chuyên đề: Phương pháp diện tích - Tạ Phạm Hải", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Chuyên đề hình 8 : phương pháp diện tích Người viết : Tạ Phạm Hải Giáo viên trường THCS Thị trấn Hưng hà - Thái bình A.Bài tập hình thành phương pháp Bài tập 1 : Cho tam giác ABC cân tại A . Gọi M là một điểm bất kì trên đáy BC . Gọi H , K thứ tự là hình chiếu của M trên AB , AC và BI là đường cao của tam giác ABC. Chứng minh : MH + MK = BI Giải: Cách 1 : Cách 2 : Nối AM và gọi S là diện tích của tam giác ABC , ta có : S = SABM + SACM = 0,5.MH.AB + 0,5.MK.AC = 0,5.AC.( MH + MK ), Vì AB = AC mà S = 0,5 BI.AC nên 0,5 BI.AC = 0,5.AC.( MH + MK ). Vậy MH + MK = BI ( đpcm ) Bài tập 2 : Cho hình thang ABCD ( AB // CD ) , hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với hai đáy cắt các cạnh bên AD , BC thứ tự ở E và F. Chứng minh : EO = FO Giải : Cách 1 : Vì OF // AB nên ; Vì OE // AB nên ( Hệ quả ĐL Ta lét ) Vì OE // DC nên (Hệ quả ĐL Ta lét ) Vậy Û OF = OE ( đpcm) Cách 2 : Đặt AD1 = BC1 = h1 ; E E1 = FF1 = h2 . Ta thấy : SABC = SABD , ị SAOD = SCOB ( có chung SAOB ) Û SAOE + SDOE = SBFO + SCFO Û 0,5.EO.h1+ 0,5EO.h2= 0,5.FO.h1+ 0,5.FO.h2 Û EO.( h1+ h2)/2 = FO.( h1+ h2)/2 Û EO = FO ( đpcm ) Nhận xét : Trong cách giải 2 của các bài tập trên , ta đã giải quyết bài toán hoàn toàn dựa vào việc xét diện tích của các hình mà công thức tính diện tích của chúng có liên quan tới các hệ thức cần phải chứng minh .Cách giải quyết bài toán dựa vào việc xét diện tích của các hình có liên quan như trên được gọi là phương pháp diện tích . Để rèn luyện cách giải này ta cần chú ý một vài đặc điểm sau : Không phải bài tập hình nào cũng giải được bằng phương pháp diện tích Có những bài tập chỉ giải được nhờ phương pháp diện tích Có những bài cần kết hợp cách giải thông thường với việc xét diện tích. Sau đây là các ví dụ minh họa nhận xét trên : Ví dụ 1 : Cho tam giác đều ABC cạnh a và M là một điểm bất kì ở trong tam giác . Gọi da , db , dc thứ tự là khoảng cách từ M đến các cạnh BC , AC, AB . Chứng minh rằng tổng : da + db + dc có giá trị không phụ thuộc vào cách chọn điểm M trong tam giác ABC Giải : Gọi hình chiếu vuông góc của M trên AB , AC , BC thứ tự là F , E , D . Khi đó dặt MD , ME , MF thứ tự là da , db , dc và nối M với A , B , C . Ta có SAMB + SBMC + SAMC = SABC Û 2SAMB + 2SBMC + 2SAMC = 2SABC Hay AB.MF + BC.MD + AC.ME = BC.AH Û BC.dc + BC.da + BC.db = BC.h Û BC(da + db + dc) = BC.h Û da + db + dc = h Vì h không đổi nên từ đó ta có điều phải chứng minh . Ví dụ 2 : Trong tam giác ABC lấy tùy ý điểm O. Goi da , db , dc thứ tự là khoảng cách từ O đến các cạnh BC , AC , AB và gọi h a , hb ,hc thứ tự là các đường cao hạ xuống BC , AC , AB . Chứng minh rằng : Giải tóm tắt : Từ hình vẽ trên ta có : Û ( Vì sao ? Bạn hãy tự giải thích ) Ví dụ 3 : Cho tam giác ABC . Tìm điểm M trong tam giác sao cho biểu thức : K = MA.BC + MB.AC + MC.AB đạt giá trị nhỏ nhất. Giải : Cộng các bất đẳng thức trên ta có MA.BC + MB.AC + MC.AB ≥ 4SABC , dấu bằng xảy ra khi M là trực tâm của DABC. Vậy giá trị nhỏ nhất của K là 4SABC khi M là trực tâm của tam giác ABC Các ví dụ 1, 2, 3 là các bài chỉ giải bằng phương pháp diện tích là thuận lợi ! Ví dụ 4 : Cho tam giác ABC có các đường cao AD , BE , CF cắt nhau tại H . Chứng minh rằng : Nếu BC + AD = AC + BE = AB + CF thì tam giác ABC là tam giác đều Giải : Trước hết cần nhận xét rằng đẳng thức kép BC + AD = AC + BE = AB + CF có các vế tương tự nhau đều là tổng của cạnh đáy và đường cao tương ứng với cạnh đáy đó , vì vậy ta chỉ cần xét một trường hợp rồi tương tự cho các trường hợp còn lại . Chẳng hạn ta xét BC + AD = AC + BE Ta có BC + AD = AC + BE Û ( BC + AD )2= ( AC + BE)2 Û BC2 + AD2 + 2.BC.AD = AC2 + BE2 + 2.AC.BE (1) Mà 2.BC.AD = 2.AC.BE = 4.SABC nên từ (1) ta có BC2 + AD2 = AC2 + BE2 Û BC2 – BE2 = AC2 – AD2 Û CE2 = CD2 Û CE = CD . Từ đó ∆VCBE = ∆VCAD ị CB = CA vậy ∆ABC cân tại C . Hoàn toàn tương tự ta có ∆ABC cân tại A và B nên nó là tam giác đều ở ví dụ 4 ta đã giải quyết bằng cách kết hợp cách giải thông thường với việc xét diện tích ; Rõ ràng là tổng của cạnh đáy và đường cao tương ứng của tam giác đã gợi cho ta nghĩ tới việc bình phương hai vế để tạo ra diện tích ! Phương pháp diện tích thường cho các lời giải đẹp , ngắn gọn , bất ngờ đầy thú vị . Việc nắm thành thạo phương pháp này ngay từ lớp 8 sẽ rất thuận lợi khi học hình học ở các lớp trên . Bài viết này mới chỉ đưa ra một khởi đầu đơn giản mà thôi . Bài tập luyện tập phương pháp Bài tập 1 : Cho tam giác ABC và điểm O bất kì trong tam giác . Qua O kẻ đường thẳng song song với AB cắt BC , AC thứ tự ở E , D ;kẻ đường thẳng song song với AC cắt AB , BC thứ tự ở F , K ; kẻ đường thẳng song song với BC cắt AB , AC thứ tự ở M , N . Chứng minh : Bài tập 2 : Cho tam giác ABC và điểm O bất kì trong tam giác . Vẽ các tia AO , BO , CO thứ tự cắt các cạnh BC , AC , AB tại D , E , K . Chứng minh : Bài tập 3 : Cho tam giác có hai cạnh là a và b . Tổng chiều cao ứng với hai cạnh ấy bằng chiều cao ứng với cạnh thứ ba . Tính cạnh thứ ba đó theo a và b . Giải : Gọi chiều cao ứng với các cạnh a , b thứ tự là ha , hb .Gọi cạnh thứ ba là c và chiều cao ứng với nó là hc .Theo bài ra ta có : ha + hb = hc (1) .Gọi diện tích tam giác ABC là S ,ta có 2S = aha = bhb = chc . Từ đó suy ra ha = 2S/a ; hb = 2S/b ; hc = 2S /c , thế vào (1) ta được : 2S/a + 2S/b = 2S/c Û 1/a + 1/b = 1/c .Vậy c = ab / ( a + b ) Bài tập 4 : Cho điểm P nằm trong tam giác ABC . Chứng ming rằng tổng các khoảng cách từ P tới ba cạnh tam giác không nhỏ hơn chiều cao nhỏ nhất và không lớn hơn chiều cao lớn nhất của tam giác ABC Bài tập 4 : Cho DABC nhọn , vẽ các đường cao BD và CE.Gọi K , L thứ tự là hình chiếu của B , C trên đường thẳng ED . Chứng minh rằng : a ) EL = DK b ) SBEC + SBDC = SBKLC Gợi ý giải : 1.Gọi N , M thứ tự là trung điểm của ED và BC thì từ DEMD cân tại M suy ra MN ^ KL nên MN là đường trung bình của hình thang vuông BKLC , ị KN = NL mà ND = NE , do đó ta có KN + ND = NL + NE hay KD = EL 2. Gọi F , R , Q thứ tự là hình chiếu của E , N , D trên BC . Dễ thấy NR = ( FE+ DQ ) : 2 . SBEC + SBDC = BC.( FE + DQ ) : 2 = NR.BC Qua N kẻ đường thẳng Qua N kẻ đường thẳng song song với BC cắt các đường thẳng BK và CL thứ tự ở T và P , ta có tứ giác BTPC là hình bình hành có diện tích bằng BC.NR Mặt khác dễ chứng minh được DKTN = DPLN ( g – c – g ) nên dễ suy ra diện tích hình bình hành BTPC bằng SBKLC. Vậy ta có SBEC + SBDC = SBKLC ( đpcm ) Bài tập 6 : Bên trong tam giác ABC lấy điểm M và gọi D , E , F thứ tự là giao điểm của MA , MB , MC với các cạnh đối của các góc A , B , C .Chứng minh rằng : Tổng S = và tích P = đạt giá trị nhỏ nhất khi M là trọng tâm của tam giác ABC . Gợi ý giải : Ta có : = = ị Tương tự : Cộng ba đẳng thức trên ta được phương hướng giải quyết bài toán. Bài tập 7 : Chứng minh rằng : a ) Nếu a , b là độ dài hai cạnh của DABC thì SABC ≤ ( a2 + b2 ) : 4 b) Nếu a , b , c , d là độ dài các cạnh và x , y là độ dài các đường chéo của tứ giác ABCD thì SABCD ≤ ( a2 + b2 + c2 + d2 ) : 4 và SABCD ≤ ( x2 + y2 ) : 4 Gợi ý giải : a ) SABC = ah / 2 ≤ ab/2 ≤ ( a2 + b2 ) / 4 . Dấu bằng xảy ra khi DABC vuông cân tại góc chen giữa hai cạnh a , b b ) Chia tứ giác thành hai tam giác bởi một đường chéo. Đẳng thức xảy ra khi tứ giác ABCD là hình vuông ; ý sau SABCD = ( x2 + y2 ) : 4 khi hai đường chéo của tứ giác vuông góc với nhau . Bài tập 8 : Cho DABC có các cạnh là a , b , c và các đường cao tương ứng với chúng là ha , hb , hc . Cho a > b . Chưng minh ha < hb Chưng minh a + ha ≥ b + hb Bài tập 9 : Cho AD , BE , CF là ba doạn thẳng đồng quy tại điểm M trong tam giác ABC ở đó D ẻ BC ; E ẻ AC ; F ẻ AB . Chứng minh rằng : Bài tập 10 : Cho hình thang ABCD ( AB // CD ) . Gọi M , N thứ tự là trung điểm của các đoạn thẳng AB , CD . Vẽ đường thẳng song song với hai đáy của hình thang cắt các cạnh bên AD , BC thứ tự tại E , F , cắt MN tại O .Chứng minh EO = FO
Tài liệu đính kèm:
 Boi duong HSGT8 Phuong phap Dien tich.doc
Boi duong HSGT8 Phuong phap Dien tich.doc





