Bài tập ôn tập Hình học Lớp 8 - Trường THCS Tượng Lĩnh
Hướng dẫn:
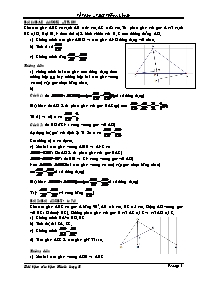
a) chứng minh hai tam giác trên đồng dạng theo
trường hợp g.g hay trường hợp hai tam giác vuông
có một cặp góc nhọn bằng nhau.
b)
Cách 1: do (tỉ số đồng dạng)
Mặt khác do AD là tia phân giác của góc BAC(gt) nên
Từ (1) và (2) ta có
Cách 2: do BD // CN ( cùng vuông góc với AD)
Ap dụng hệ quả của định lý Ta lét ta có
Cm tương tự ta có đpcm.
c) Xét hai tam giác vuông AMB và ANC có
( Do AD là tia phân giác của góc BAC)
( do BM và CN cùng vuông góc với AD)
Nên (hai tam giác vuông có một cặp góc nhọn bằng nhau)
(tỉ số đồng dạng)
Mặt khác (tỉ số đồng dạng)
Vậy (vì cùng bằng )
Bạn đang xem tài liệu "Bài tập ôn tập Hình học Lớp 8 - Trường THCS Tượng Lĩnh", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Bài 1:(BÀI 44/SGK –TR 80) Cho tam giác ABC có cạnh AB = 24 cm, AC = 28 cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B, C trên đường thẳng AD. Chứng minh tam giác AMD và tam giác AND đồng dạng với nhau. Tính tỉ số Chứng minh rằng Hướng dẫn: chứng minh hai tam giác trên đồng dạng theo trường hợp g.g hay trường hợp hai tam giác vuông có một cặp góc nhọn bằng nhau. Cách 1: do (tỉ số đồng dạng) Mặt khác do AD là tia phân giác của góc BAC(gt) nên Từ (1) và (2) ta có Cách 2: do BD // CN ( cùng vuông góc với AD) Aùp dụng hệ quả của định lý Ta lét ta có Cm tương tự ta có đpcm. Xét hai tam giác vuông AMB và ANC có ( Do AD là tia phân giác của góc BAC) ( do BM và CN cùng vuông góc với AD) Nên (hai tam giác vuông có một cặp góc nhọn bằng nhau) (tỉ số đồng dạng) Mặt khác (tỉ số đồng dạng) Vậy (vì cùng bằng ) Bài 2:(Bài 42/SBT- tr 74) Cho tam giác ABC có góc A bằng 900, AB = 3 cm, BC = 5 cm. Dựng AD vuông góc với BC ( D thuộc BC). Đường phân giác của góc B cắt AC tại E và cắt AD tại F. Chứng minh BA2 = BD. BC Tính độ dài EA, EC. Chứng minh . Tam giác AFE là tam giác gì? Vì sao. Hướng dẫn: Xét hai tam giác vuông ADB và ABC có Vậy (Tỉ số đồng dạng) hay AB2 = BD.BC Do BE là tia phân giác của góc ABC Nên ( Tính chất đường phân giác trong tam giác) Mà AB = 3 cm, BC = 5 cm nên Do tam giác ABC vuông tại A nên theo định lý PITAGO ta có AC2 = BC2 – AB2 = 52 – 32 = 16 -> AC = 4 cm. Vậy -> EA = 1,5cm; EC = 2,5 cm. Xét tam giác ABD có BF là phân giác của góc B nên ( Tính chất đường phân giác trong tam giác). Xét tam giác ABC có AE là phân giác của góc B nên ( Tính chất đường phân giác trong tam giác) Mà (cm ở ý a)Vậy Xét hai tam giác DBF và ABE có (do AE là tia phân giác của góc B) Vậy( hai góc tương ứng) (đối đỉnh) -> -> tam giác AFE cân tại A. Bài 3:(Bài tập/ đề thi năm 08-09) Cho tam giác ABC vuông đỉnh A, đường cao AH. Biết AB = 6 dm, AC = 8 dm. Viết tên tất cả các tam giác đồng dạng với tam giác HCA. Chứng minh AC2 = HC.BC. Đường phân giác của góc ACB cắt cạnh AB tại điểm K. Tính tỉ số Gọi giao điểm của AH với CK là E. Tính diện tích tam giác HCE. Hướng dẫn: Xét hai tam giác CHA và CAB có: Xét hai tam giác BHA và BAC có Do vậy ( tính chất bắc cầu) Chứng minh tương tự ý a bài 2. Do CK là đường phân giác của góc C (gt) nên ( tính chất đường phân giác trong tam giác) mà AB = 6 dm, AC = 8 dm Áp dụng định lý Pitago vào tam giác vuông ABC ta có: BC2 = AB2 + AC2 = 62 + 82 = 100 -> BC = 10 cm Vậy d)Ta có và HB = BC – HC = 10-6,4 = 3,6 cm Lại có (cmt) Ta có ( Tính chất đường phân giác trong tam giác ACH) (cm) Vậy SHCE = Bài 4:(Bài 47,50/SBT- tr 75) Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết BH = 4cm, HC = 9cm Chứng minh AH2 = BH.HC Tính diện tích tam giác AMH. Từ M kẻ MN vuông góc với AC. Tính độ dài đoạn thẳng MN. Hướng dẫn: Xét tam giác AHB và tam giác AHC ta có Mặt khác do tam giác ABC vuông tại A nên Tam giác AHC vuông tại H nên Vậy (tỉ số đồng dạng) hay AH2 = BH.HC Ta có AH2 = BH.HC = 4.9 = 36 cm -> AH = 6 cm BC = BH + HC = 4+9 = 13 cm -> BM = MC = 7,5 cm. Cách 1: SABM = ; SABH = Vậy SAHM = SABM – SABH = 22,5 – 12 = 10,5 cm2 Cách 2: HM = BM – BH = 7,5 – 4 = 3,5 cm Vậy SAHM = ta có MN // AB ( cùng vuông góc với AC) Theo hệ quả của định lí Ta lét ta có Cm hai tam giác ABH và ABC đồng dạng( tương tự ý a bài 42) -> AB2 = BH.BC -> AB2 = 4.13 -> AB = Bài 5: Cho D ABC ( ) và đường phân giác AD (D BC).Từ D kẻ DEAC(EAC). a)Chứng minh : D ABC ~D EDC. b)Qua E kẻ EK song song AD(KBC).Chứng minh : Hướng dẫn: b) do EK // AD (gt) nên (1)( định lí Ta lét) và DE // AB ( cùng vuông góc với AC) nên (2) Do AD là đường phân giác góc A của tam giác ABC (gt) Nên (3)( tính chất đường phân giác của tam giác) Vì D ABC ~D EDC (cmt) nên (4) ( tỉ số đồng dạng) Từ (1)(2)(3)(4) ta có Bài 6 : Cho ABC vuông ở A , có AB = 6cm , AC = 8cm .Vẽ đường cao AH . Tính BC Chứng minh ABC ~AHB Chứng minh AB2 = BH.BC .Tính BH , HC Vẽ phân giác AD của góc A ( D BC) .Tính DB Bài 7:Cho tam giác ABC vuông tại A . Dựng AH vuông góc với BC ( H Ỵ BC ) sao cho HB = 9cm , HC = 16cm . Đường phân giác BE cắt AH tại F . a) Chứng minh : DABH ~ DCAH . b) Tính AH . c) Chứng minh : FH . EC = EA . FA d) Từ E kẻ đường thẳng song song với AB cắt BC tại D Chứng minh : Bài 8:(Bài 58/SGK-TR92) Cho tam giác cân ABC (AB = AC) .Vẽ các đường cao BH , CK , AI . Chứng minh BK = CH Chứng minh KH //BC Chứng minh HC.AC = IC.BC Cho biết BC = a , AB = AC = b . Tính độ dài đoạn thẳng HK theo a và b . c)cm hai tam giác BHC và AIC đồng dạng. d) Tính HC rồi tính AH. Theo hệ quả của định lí Ta lét ta cĩ Bài 9 Cho ABC , các đường cao BD , CE cắt nhau tại H .Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K .Gọi M là trung điểm của BC . Chứng minh Chứng minh HE.HC = HD.HB Chứng minh H , K , M thẳng hàng ABC phải có điều kiện gì thì tứ giác BHCK là hình thoi ? Hình chữ nhật ? Hướng dẫn: b) Vì (cmt) nên (góc tương ứng) Chứng minh hai tam giác vuông EBH và DCH đồng dạng (g.g) -> đpcm c) Chứng minh BHCK là hình bình hành, dùng tính chất hai đường chéo -> đpcm d) Vì BHCK là hình bình hành +) BHCK là hình thoi khi BC là đường phân giác của các góc Vì BHCK là hình thoi nên Vậy tam giác ABC cân tại A thì BHCK là hình thoi. +) Là hình chữ nhật khi Tứ giác AEHD có ba góc vuông là hình chữ nhật nên Vậy tam giác ABC vuông tại A thì BHCK là hình chữ nhật (khi đó E,D,H trùng với A) Bài 10:Cho góc xOy khác khóc bẹt.Trên tia Ox đặt các đoạn thẳng OA= 5cm ,OB=16 cm Trên tia Oy dặt các đoạn thẳng OC = 8cm ,OD = 10cm. a)Chứng minh : D OCB ~D OAD. b)Gọi I là giao điểm của AD và BC. Chứng minh : AI . ID = IB . IC c) Tính tỉ số diện tích của hai tam giác ICD và IAB. Bài 11 :Cho góc xAy khác khóc bẹt.Trên tia Ax đặt các đoạn thẳng AE = 3cm,AC =8 cm Trên tia Ay dặt các đoạn thẳng AD = 4cm ,AF = 6cm. a)Chứng minh : D ACD ~D AFE. b)Gọi I là giao điểm của CD và EF.Tính tỉ số diện tích của hai tam giác IDF và IEC. Bài 12:Cho hình thang ABCD(AB // CD).Goi O là giao điểm của AC và BD. a)Chứng minh : OA . OD = OB . OC. b)Đường thẳng qua O vuông góc vói AB và CD theo thứ tự tại H và K. Chứng minh : Bài 14: Cho hình thang ABCD có AB // CD và AB < CD, đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH. Chứng minh D BDC ∽ D HBC Cho BC = 15cm, DC = 25cm. Tính HC, HD. Tính diện tích hình thang ABCD. Bài 15: Cho hình thang ABCD (AB // CD ) , hai đường chéo cắt nhau tại I Chứng minh : IA.ID = IB .IC Chứng minh IAD ∽ IBC. Bài 16 : Cho hình thang ABCD ( AB // CD ) . Hai cạnh bên DA và DB cắt nhau tại S . Chứng minh : Tam giác SAB đồng dạng với tam giác SDC . Gọi M là giao điểm của hai đường chéo AC và BD . Từ M kẽ MN // AB ( N Ỵ BC ) Chứng minh : . Bài 17:Cho hình thang ABCD ( AB // CD và AB<CD),hai cạnh bên DA và CB cắt nhau tại S.Gọi M là trung điểm của AB ( SM cắt DC tại N). Chứng minh: D SAB ~D SDC. SN là đường trung tuyến của D SDC. Bài 18 : Cho hình thang vuông ABCD () có AC cắt BD tại O . Chứng minh OABOCD, từ đó suy ra Chứng minh AC2 – BD2 = DC2 – AB2 Bài 19 : Cho hình thanh cân ABCD có AB // Dc và AB< DC , đường chéo BD vuông góc với cạnh bên BC .Vẽ đường cao BH , AK . Chứng minh BDC HBC Chứng minh BC2 = HC .DC Chứng minh AKD BHC Cho BC = 15cm , DC = 25 cm .Tính HC , HD . Tính diện tích hình thang ABCD. Bài 20 : Cho hình chữ nhật ABCD.Vẽ đường cao AH của D ADB.Chứng minh : D AHB ~D BCD. AD2 = DH . DB Vẽ đường cao CK của D DBC(K DB),phân giác HM của D AHB(MAB),phân giác KN của D CKD.Chứng minh : Bài 21: Cho hình chữ nhật ABCD có AB = 8cm , BC = 6cm .Vẽ đường cao AH của ADB . a) Tính DB b) Chứng minh ADH ~ADB c) Chứng minh AD2= DH.DB d) Chứng minh AHB BCD e) Tính độ dài đoạn thẳng DH , AH Bài 22:Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O, . Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng: a. DAOB ~ DDOC b. DAOD ~ DBOC c. EA . ED = EB . EC
Tài liệu đính kèm:
 BAI TAP HINH HOC 8 ON TAP CUOI NAM CO SUU TAM.doc
BAI TAP HINH HOC 8 ON TAP CUOI NAM CO SUU TAM.doc





