Bài giảng Tin học 8 - Bài 4: Bài toán và thuật toán

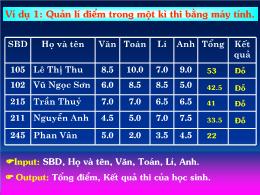
SBDHọ và tênVănToánLíAnhTổngKết quả105Lê Thị Thu 8.510.07.09.0102Vũ Ngọc Sơn6.08.58.55.0215Trần Thuỷ7.07.06.56.5211Nguyễn Anh 4.55.07.07.5245Phan Vân5.02.03.54.5Ví dụ 1: Quản lí điểm trong một kì thi bằng máy tính. Yêu cầu : 	Hãy xác định thông tin đưa vào (Input) 	 và thông tin cần lấy ra (Output) Input: SBD, Họ và tên, Văn, Toán, Lí, Anh.  Output: Tổng điểm, Kết quả thi của học sinh. 53Đỗ42.5Đỗ41Đỗ33.5Đỗ22Ví dụ 2: Giải phương trình bậc nhất ax + b = 0. Yêu cầu : 	Hãy xác định thông tin đưa vào (Input) 	 và thông tin cần lấy ra (Output) Input: Các hệ số a, b.  Output: Nghiệm của phương trình. Với a = 1, b = -5  Phương trình có nghiệm x = 51. Khái niệm bài toán Là việc nào đó ta muốn máy thực hiện để từ thông tin đưa vào (INPUT) tìm được thông tin ra (OUTPUT). Ví dụ 3: Tìm ước số chung lớn nhất của hai số nguyên dương.	INPUT: Hai số nguyên dương M và N.	OUTPUT: ước số chung lớn nhất của M và N.Ví dụ 4: Bài toán xếp loại học tập của một lớp. 	INPUT: Bảng điểm của học sinh trong lớp. 	OUTPUT: Bảng xếp loại học lực của học sinh. Bài 4. Bài toán và thuật Toán2. Khái niệm thuật toán Từ INPUT làm thế nào để tìm ra OUTPUT ?Các em cần tìm ra cách giải của bài toán. Xét ví dụ 2: Giải phương trình bậc nhất ax + b = 0. B1: Xác định hệ số a, b;B2: Nếu a=0 và b=0 => Phương trình vô số nghiệm =>B5;B3: Nếu a=0 và b≠0 => Phương trình vô nghiệm =>B5;B4: Nếu a≠0 => Phương trình có nghiệm x=-b/a =>B5;B5: Kết thúc. Thuật toán để giải một bài toán là một dãy hữu hạn các thao tác được sắp xếp theo một trình tự xác định sao cho sau khi thực hiện dãy thao tác ấy, từ Input của bài toán, ta nhận được Output cần tìm. Có hai cách thể hiện một thuật toán: 	 Cách 1: Liệt kê các bước. 	 Cách 2: Vẽ sơ đồ khối.B7: Kết thúc. B1: Bắt đầu; B2: Nhập a, b, c; B3: Tính  = b2 – 4ac; B4: Nếu  PT vô nghiệm => B7; B5: Nếu  = 0 => PT có nghiệm kép x = -b/2a => B7; B6: Nếu  > 0 => PT có hai nghiệm x1, x2 = (-b  )/2a  => B7;3. Một số ví dụ về thuật toán Thuật toán giải phương trình bậc hai (a  0). Cách 1: Liệt kê các bướcQuy ước các khối trong sơ đồ thuật toánBắt đầu thuật toán. Dùng để nhập và xuất dữ liệu.Dùng để gán giá trị và tính toán.Xét điều kiện rẽ nhánh theo một trong hai điều kiện đúng, sai.Kết thúc thuật toán. BĐ ĐKđSKTCách 2: Vẽ sơ đồ khốiNhập vào a, b, cD= b-4acD Max thì Max nhận giá trị mới là ai.Cách 1: Liệt kê các bước B1: Nhập N và dãy a1,, aN; B2: Max  a1; i  2; B3: Nếu i > N thì đưa ra giá trị Max rồi kết thúc; B4:	Bước 4.1: Nếu ai > Max thì Max  ai;	Bước 4.2: i  i+1 rồi quay lại B3.ĐSĐSNhập N và dãy a1,,aNMax  a1 ; i  2i > N ?ai > Max ? Max  aii  i + 1Đưa ra Max rồi kết thúc B1: Nhập N và dãy a1,,aN; B2: Max  a1; i  2; B3: Nếu i > N thì đưa ra giá trị  Max rồi kết thúc; B4 : 4.1: Nếu ai > Max thì Max  ai; 4.2: i  i + 1 rồi quay lại B3.Cách 2: Sơ đồ khốiĐSĐSNhập N và dãy a1,,aNMax  a1 ; i  2I > N ?ai> Max ? Max aii  i+1Đưa ra Max rồi kết thúcMaxiA77555543267415N=5 ; A [ 5 1 4 7 6 ]Max  5 ; i  22 > 5 ?1> 5 ?i  2+13 > 5 ?4> 5 ?i 3+14 > 5 ?7 > 5 ? Max 74i 4+15 > 5 ?7 > 7 ?i 5+16 > 5 ?Số lớn nhất của dãy là 7Mô phỏng thuật toán Với i = 2Với i = 3Với i = 4Với i = 5ĐSĐSNhập N và dãy a1,,aNMax  a1 ; i  2I > N ?ai> Max ? Max aii  i+1Đưa ra Max rồi kết thúcMaxiA77555543267415N=5 ; A [ 5 1 4 7 6 ]Max  5 ; i  22 > 5 ?1> 5 ?i  2+13 > 5 ?4> 5 ?i 3+14 > 5 ?7 > 5 ? Max 74i 4+15 > 5 ?7 > 7 ?i 5+16 > 5 ?Số lớn nhất của dãy là 7Thuật toán kiểm tra tính nguyên tố của một số nguyên dương Xác định bài toán: INPUT: N là một số nguyên dương. OUTPUT: Trả lời câu hỏi N có là số  nguyên tố không?ý tưởng: Xét các trường hợpCác em hãy nêu định nghĩa số nguyên tố. - Nếu N  4 và không có ước số trong phạm vi từ 2 đến phần nguyên căn bậc hai của N thì N là số nguyên tố. - Nếu N = 1 thì N không là số nguyên tố.- Nếu 1 [N ] thì thông báo N là nguyên tố, kết thúc;B6: Nếu N chia hết cho i thì thông báo N không nguyên 	tố rồi kết thúc; B7: i  i +1 rồi quay lại B5.Nhập NN =1 ?N [N ] ?N có chia hết cho i ?i  i +1Thông báo N là số nguyên tố rồi kết thúc.Thông báo N không là số nguyên tố rồi kết thúc. ĐSSĐSSĐĐCách 2 Vẽ sơ đồ khốiThuật toán sắp xếp Hãy tìm cách sắp xếp học sinh đứng chào cờ (hình a) theo thứ tự thấp trước cao sau (hình b).Hình aHình bThuật toán sắp xếp bằng tráo đổi Xác định bài toán:INPUT: Dãy A gồm N số nguyên a1, a2,, aN.OUTPUT: Dãy A được sắp xếp thành dãy không giảm. ý tưởng: Với mỗi cặp số hạng đứng liền kề trong dãy, nếu số trước lớn hơn số sau ta đổi vị trí chúng cho nhau. Việc đó được lặp lại cho đến khi không có sự đổi chỗ nào xảy ra nữa.  Với N = 6 và dãy A gồm 6 số hạng như sau : 359817 Lượt thứ nhất: 359817358917358197358179 Lượt thứ hai: 358179351879351789 Lượt thứ ba: 351789315789315789135789 Lượt thứ tư: Mô phỏng thuật toán sắp xếp bằng tráo đổiCách 1: Liệt kê các bướcB1: Nhập N, các số hạng a1, a2,, aN;B2: M  N;B3: Nếu M M thì quay lại B3;B7: Nếu ai > ai+1 thì tráo đổi ai và ai+1 cho nhau;B8: Quay lại B5.Nhập N và a1, a2,..., aN M  NM M ?ai > ai+1 ?Tráo đổi ai và ai+1Đưa ra A đã sắp xếprồi kết thúcĐĐĐSSSCách 2 Vẽ sơ đồ khốiThuật toán tìm kiếmHai bạn chó (Bi và Bông) chơi trốn tìm, Bông đã trốn vào một trong những chiếc mũ của ông già Nôen trên. Hãy chỉ ra các cách tìm chiếc mũ mà Bông đang trốn? Cho biết có những cách nào?Bông trốn đâu nhỉ ?C1: Tìm kiếm tuần tự ( mở từng mũ)C2: Do các mũ đã sắp xếp lớn dần, hai mũ đầu nhỏ hơnngười của Bông nên chỉ tìm hai mũ sau thôi!Thuật toán tìm kiếm tuần tự Xác định bài toán: INPUT: Dãy A gồm N số nguyên a1, a2,, aN đôi một khác nhau và số nguyên k. OUTPUT: Chỉ số i mà ai = k hoặc thông báo không có số hạng nào của A bằng k. 54321I5125118924175A Mô phỏng thuật toán tìm kiếm tuần tự  Với k = 2 và dãy A gồm 10 số hạng như sau: Tại vị trí i = 5 có a5 = 2 = k Với k = 6 và dãy A gồm 10 số hạng như sau: A5714298112551I1234567891011 Với mọi i từ 1 10 không có ai có giá trị bằng 6 5ý tưởng: 	Lần lượt từ số hạng thứ nhất, ta so sánh giá trị số hạng đang xét với khoá (k) cho đến khi có sự trùng nhau, nếu đã xét tới số hạng cuối cùng mà không có sự trùng nhau thì có nghĩa là dãy A không có số hạng nào có giá trị bằng k. Cách 1: Liệt kê các bước Bước 1: Nhập N, các số hạng a1, a2,, aN  và giá trị khoá k; Bước 2: i  1; Bước 3: Nếu ai = k thì thông báo chỉ số i, rồi kết thúc; Bước 4: i  i+1; Bước 5: Nếu i > N thì thông báo dãy A không có số hạng nào có giá trị bằng k, rồi kết thúc; Bước 6: Quay lại B3.Nhập N, a1, a2,..., aN và ki  1ai = k ?Đưa ra irồi kết thúcĐSĐi i + 1i > N ?Thông báo dãy A không có số hạng có giá trị bằng k, rồi kết thúcSCách 2 Vẽ sơ đồ khốiThuật toán tìm kiếm nhị phân ý tưởng: Sử dụng tính chất dãy A đã sắp xếp tăng, ta tìm cách thu hẹp nhanh phạm vi tìm kiếm bằng cách so sánh k với số hạng ở giữa dãy (agiữa), khi đó chỉ xảy ra một trong ba trường hợp: 	- Nếu agiữa= k => tìm được chỉ số, kết thúc;	- Nếu agiữa > k => do dãy A đã được sắp xếp tăng 	 nên việc tìm kiếm thu hẹp chỉ xét từ a1  agiữa - 1; 	- Nếu agiữa do dãy A đã được sắp xếp tăng 	 nên việc tìm kiếm thu hẹp chỉ xét từ agiữa + 1  aN.Quá trình trên được lặp đi lặp lại cho đến khi tìm được OUTPUT.Mô phỏng thuật toán tìm kiếm nhị phân 10987654321i333130222196542A Với k = 21 và dãy A gồm 10 số hạng như sau: Lượt thứ nhất: agiữa là a5 = 9; 9 21 vùng tìm kiếm thu hẹp trong phạm vi từ a6 a7;Lượt thứ ba: agiữa là a6 = 21; 21= 21 	 Vậy số cần tìm là i = 6.22216621 Liệt kê các bước Bước 1: Nhập N, các số hạng a1, a2,, aN  và giá trị khoá k; Bước 2: Đầu  1, Cuối  N; Bước 3: Giữa  [(Đầu + Cuối)/2]; Bước 4: Nếu aGiữa = k thì thông báo chỉ số Giữa 	 rồi kết thúc; Bước 5: Nếu aGiữa > k thì đặt Cuối = Giữa - 1 rồi	 chuyển sang bước 7; Bước 6: Đầu  Giữa + 1; Bước 7: Nếu Đầu  Cuối thì thông báo dãy A không có số hạng có giá trị bằng k, rồi kết thúc; Bước 8: Quay lại bước 3.1. Khái niệm bài toán Bài toán và thuật Toán2. Khái niệm thuật toán Thuật toán giải phương trình bậc hai (a 0). Thuật toán tìm Max của một dãy số.Thuật toán kiểm tra tính nguyên tố của một số nguyên dương.Thuật toán sắp xếp bằng tráo đổi. Thuật toán tìm kiếm tuần tự và nhị phân.