Thi chọn học sinh giỏi Lớp 9 THCS giải toán bằng máy tính Casio năm học 2008-2009

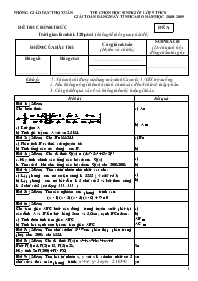
PHềNG GIÁO DỤC THỌ XUÂN 	 THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
 	GIẢI TOÁN BẰNG MÁY TÍNH CASIO NĂM HỌC 2008- 2009
 ĐỀ THI CHÍNH THỨC	ĐỀ A
Thời gian làm bài: 120 phỳt (khụng kể thời gian phỏt đề)
ĐIỂM CỦA BÀI THI
Cỏc giỏm khảo
(Họ tờn và chữ ký)
SỐ PHÁCH
(Do chủ tịch hội đồng chấm thi ghi)
Bằng số
Bằng chữ
..
.
..
Chỳ ý:	 1. Thớ sinh chỉ được sử dụng mỏy tớnh Casio fx-570ES trở xuống.
	2. Nếu khụng núi gỡ thờm hóy tớnh chớnh xỏc đến 8 chữ số thập phõn.
3. Chỉ ghi kết quả vào ụ và khụng thờm ký hiệu gỡ khỏc.
Đề bài
Kết quả
Bài 1: (2điểm)
Cho biểu thức:
a) Rút gọn A 
b) Tính giá trị của A với x=2,3154 
a) A=
b) A
Bài 2: (2điểm) Cho B=888241
a) Phân tích B ra thừa số nguyên tố.
b) Tính tổng các ước dương của B. 
a)B=
b)
Bài 3: (2điểm) Cho đa thức Q(x) = (4x3-3x2+6x-2)20
a. Hãy tính chính xác tổng các hệ số của Q(x)
b. Tìm số dư khi chia tổng các hệ số của Q(x) cho 20082008
a)
b)
Bài 4: (2điểm) Tìm số tự nhiên nhỏ nhất sao cho: 
a) Lập phương của nó có tận cùng là 3333 ( 4 chữ số 3)
b) Lập phương của nó bắt đầu là 3 chữ số 3 và kết thúc cũng là 3 chữ số 3 (có dạng 333...333 )
a)
b)
Bài 5: (2điểm) Tìm các nghiệm của phương trình sau:
 (x - 1)(x - 3)(x - 4)(x - 6) + 9 = 0
Bài 6: (2điểm)
Cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm và 3,6cm; cạnh BC= 4cm.
a) Tính diện tính tam giác ABC
b) Tính hai cạnh còn lại của tam giác ABC 
a) 
b) 
AB
AC
Bài 7: (2điểm) Tìm chữ số thứ 52009 của phần thập phân trong phép chia 2008 cho 8534
Bài 8: (2điểm) Cho đa thức P(x)= x4+ax3+bx2+cx+d
Biết P(1)=4; P(2)=13; P(3)=28; 
Hãy tính S=P(200)+P(-196)
S=
Bài 9: (2điểm) Tìm hai tự nhiên x, y với x là số nhỏ nhất có 3 chữ số và thoả mãn phương trình: x3+x2-y2-2xy+x -2103=0 
x=
y=
Bài 10: (2điểm) 
Một giải thi đấu cờ vua có khoảng 20 đến 30 người tham dự, trong đó có các kiện tướng và các vận động viên (chưa được phong cấp kiện tướng). Theo thể lệ thi đấu vòng tròn (mỗi người đấu với một người khác một trận) ai thắng được 2 điểm, thua 0 điểm còn hoà được 1 điểm. Biết rằng tổng số điểm của tất cả các đấu thủ giành được trong trận đấu mà có kiện tướng tham gia thì bằng nửa tổng số điểm của tất cả mọi người tham gia giải.
Hỏi có bao nhiêu người tham gia giải đấu và có bao nhiêu kiện tướng? 
Bài làm: (Yêu cầu trình bày vắn tắt lời giải bài 10)
.................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. .................................................................................................................................................. ..................................................................................................................................................