Ma trận và đề thi học kì I Toán Khối 8

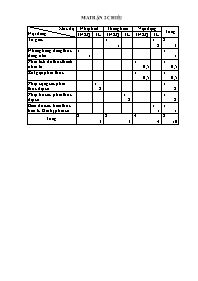
MA TRẬN 2 CHIỀU
Mức độ
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng
TNKQ
TL
TNKQ
TL
TNKQ
TL
Tứ giác
1
1
1
2
2
3
Những hằng đẳng thức đáng nhớ
1
1
1
1
Phân tích đa thức thành nhân tử
1
0,5
1
0,5
Rút gọn phân thức
1
0,5
1
0,5
Phép cộng các phân thức đại số
1
2
1
2
Phép trừ các phân thức đại số
1
2
1
2
Biến đổi các biểu thức hữu tỉ. Giá trị phân số
1
1
1
1
Tổng
2
3
2
3
4
4
8
10
ĐỀ THI HỌC KÌ I KHỐI 8
Thời gian 90 phút
TRẮC NGHIỆM KHÁCH QUAN
Câu 1: Hãy điền đúng (Đ), sai (S) vào ô trống trong các câu sau:
a. Tứ giác có hai cạnh đối vừa song song vừa bằng nhau là hình bình hành.
b. Hình thang có hai cạnh bên bằng nhau là hình thang cân.
c. Trong hình thang cân, hai cạnh bên bằng nhau.
d. Trong hình thoi, hai đường chéo bằng nhau và vuông góc với nhau.
Câu 2: Nối từ cột A đến cột B sao cho đúng
A
Nối
B
1. a2 – b2
2. a3 – b3
3. (a + b)2
4. (a + b) 3
a. a3 + 3a2b + 3ab2 + b3
b. (a + b) (a – b)
c. a2 + 2ab + b2
d. a3 – 3a2b + 3ab2 – b3
e. (a – b)(a2 + ab + b2)
Câu 3: Hãy khoanh tròn vào đáp án đúng.
Kết quả rút gọn của phân thức là:
a. 	b. 3	c. -3	d. 
Câu 4: Kết quả phân tích đa thức (x + 5)2 – 3(x + 5) thành nhân tử là:
a. (x + 5)(x + 2)	b. (x + 5)(x – 2)	c. (x – 5)(x + 2)	d. (x – 5)(x – 2)
TỰ LUẬN
Câu 1: (2 điểm) 
Phát biểu quy tắc cộng hai phân thức có mẫu thức khác nhau?
Thực hiện phép cộng sau:
Câu 2: (2 điểm) Thực hiện các phép tính sau:
a. 
b. 
Câu 3: (2 điểm) Cho hình bình hành ABCD có BC = 2AB. Gọi M, N thứ tự là trung điểm của BC và AD. Gọi P là giao điểm của AM với BN, Q là giao điểm của MD với CN.
Chứng minh rằng, tứ giác ABMN là hình thoi?
Chứng minh rằng, tứ giác PMQN là hình chữ nhật?
Câu 4: (1 điểm) Rút gọn, sau đó tính giá trị của biểu thức
 với x = 999, y = 1000.
ĐÁP ÁN
TRẮC NGHIỆM KHÁCH QUAN
Câu 1: a – Đ, b – S, c – Đ, d – S.
Câu 2: 1 – b, 2 – e, 3 – c, 4 – a.
Câu 3: b.
Câu 4: a.
TỰ LUẬN
Câu 1: 
a. Muốn cộng 2 phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi cộng các phân thức có cùng mẫu thức vừa tìm được.	(1đ)
b. Áp dụng
Câu 2: 
a. 
b. Câu 3: 
A
B
C
D
M
N
P
Q
GT ABCD là hình bình 
 hành, AN = ND, 
 BM = MC, 
 AMÇBN={P}, 
 MDÇNC={Q}
KL a. ABMN là hình thoi.
 b. PMQN là hình chữ
 nhật.
CM
a. Ta có AN = ND, BM = MC (gt) mà ABCD là hình bình hành nên MN//AB.
Mặt khác ta có BC= 2AB (gt) Þ AB = BM (gt) 
Þ ABMN là hình thoi (dấu hiệu nhận biết).
b. Xét sét DBCN, có BM = MC (gt), BP = PN (ABMN là hình thoi) Þ PM là đường trung bình của DBCN nên PM // NQ (1) và PM = NC.
Ta có tứ giác MNCD là hình thoi (chứng minh tương tự ý a), 
nên Þ NQ = QC
Þ QN = PM (2)
Từ (1) và (2) suy ra tứ giác PMQN là hình bình hành. 
Lại có ABMN là hình thoi nên BN ^ AM hay góc 
Þ PMQN là hình chữ nhật.
Câu 4:
với x = 999, y = 1000 thì biểu thức bằng