Ma trận đề kiểm tra học kì II Toán Lớp 9

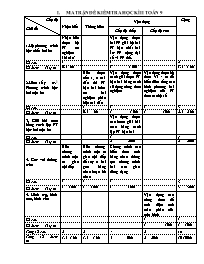
I. MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II TOÁN 9
 Cấp độ
Chủ đề 
Nhận biết
Thông hiểu
Vận dụng
Cộng
 Cấp độ thấp
Cấp độ cao
1.Hệ phương trình bậc nhất hai ẩn
Nhận biết được hệ PT có nghiệm khi nào?
Vận dụng được hai PP giải hệ hai PT bậc nhất hai ẩn: PP cộng đại số và PP thế.
Số câu 
1
1
2
Số điểm Tỉ lệ %
0,5 5%
1 1 0%
1,5 15%
2.Hàm số y = ax2. Phương trình bậc hai một ẩn
Biết được nếu a, c trái dấu thì PT bậc hai luôn có hai nghiệm phân biệt trái dấu
Vận dụng được cách giải được PT bậc hai bằng cách sử dụng công thức nghiệm
Vận dụng được hệ thức Vi - ét để biểu diễn tổng các bình phương hai nghiệm của PT theo các hệ số
Số câu 
1
1
1
3
Số điểm Tỉ lệ %
0,5 5%
1 1 0%
1 10%
2,5 25%
3. Giải bài toán bằng cách lập PT bậc hai một ẩn
Vận dụng được các bước giải bài toán bằng cách lập PT bậc hai
Số câu 
1
1
Số điểm Tỉ lệ %
2 20%
2 20%
4. Góc với đường tròn
Biết chứng minh một tứ giác nội tiếp
Biết chứng minh một tứ giác nội tiếp để suy ra hai góc bằng nhau hoặc bù nhau
Chứng minh các biểu thức tích bằng nhau thông qua chứng minh hai tam giác đồng dạng
Số câu 
1
1
1
3
Số điểm Tỉ lệ %
1 10%
1 10%
1 10%
3 30%
5. Hình trụ, hình nón, hình cầu
Vận dụng các công thức để tính diện tích toàn phần của một hình
Số câu 
1
1
Số điểm Tỉ lệ %
1 10%
1 10%
Tổng số câu 
2
2
4
2
10
Tổng số điểm %
1,5 15%
1,5 15%
5 50%
2 20%
10 100%
II. ĐỀ KIỂM TRA.
Câu 1 (1,5 đ): Giải hệ phương trình sau:
a) Không giải hệ phương trình, hãy nhận biết số nghiệm của hệ phương trình đó
b) Giải hệ phương trình
Câu 2 (2, 5 đ): Cho hàm số x2 -2mx -1 = 0 (1)
a) Giải phương trình khi m = 5
b) Chứng minh rằng phương trình luôn có hai nghiệm trái dấu với mọi m
c) Gọi x1, x2 là hai nghiệm của phương trình (1), tìm m để 
Câu 3 (2,0đ): Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 5m, diện tích bằng 300m2. Tính các kích thước của khu vườn đó.
Câu 4 (4,0 đ): Cho rABC vuông cân ở A, từ B vẽ nửa đường thẳng Bx cắt cạnh AC ở D. Kẻ CE vuông góc với Bx tại E. Các đường thẳng AB, CE cắt nhau tại F.
a) Chứng minh tứ giác ABCE nội tiếp một đường tròn.
b) Tính ?
c) Chứng minh BD.BE = BA.BF
d) Nếu , AB = a. Tính diện tích toàn phần của hình tạo bởi khi quay rBFC quanh BF.
III. ĐÁP ÁN VÀ BIỂU ĐIỂM
Câu
Nội dung
Điểm
1
a) Hệ phương trình sau: có 
nên hệ có một nghiệm duy nhất
0,25
0,25
b) 
1,0
2
a) Khi m=5 ta có phương trình là x2 - 10x - 1 = 0
Tính r' = 25 + 1 = 26
Tập nghiệm của PT là 
0,25
0,5
0,25
b) PT x2 -2mx -1 = 0 có hệ số a=1; c = -1
, chứng tỏ PT (1) có hai nghiệm trái dấu với mọi m
0,25
0,25
c) Áp dụng hệ thức Vi ét có 
Từ x1 + x2 = 2m (x1 + x2 )2 = 4m2 
0,25
0,25
0,25
0,25
3
Gọi x là chiều rộng khu vườn hình chữ nhật, (x>0,m) thì chiều dài là x+5. Vì diện tích bằng 300m2 nên ta có x(x+5) = 300
Vậy chiều rộng mảnh vườn là 15m, chiều dài là 20m
0,5
0,5
0,25
0,5
0,25
4
0,25
Hai điểm A, E cùng nhìn đoạn BC dưới một góc 900 nên bốn điểm A, B, C, E cùng thuộc một đường tròn => tứ giác ABCE nội tiếp một đường tròn
0,25
0,25
0,25
b) Tứ giác ADEF có nên ADEF nội tiếp một đường tròn 
Tứ giác ABCE nội tiếp 
0,25
0,25
0,25
0,25
c) Xét rBAD và rBEF có: 
 rBAD ∽rBEF(G.G) 
0,5
0,5
d) Diện tích toàn phần của hình tạo bởi khi quay rBFC quanh BF là Stp:
Stp = Sxq của hình chóp khi quay rABC quanh AB tạo ra + Sxq của hình chóp khi quay rACF quanh AF tạo ra.
AB=AC=a (gt) 
Sxq của hình chóp khi quay rABC quanh AB tạo ra là 
Sxq của hình chóp khi quay rACF quanh AF tạo ra là 
Trong đó 
Sxq của hình chóp khi quay rACF quanh AF tạo ra là 
Vậy 
0,25
0,25
0,25
0,25