Giáo án tự chọn môn Toán - Tiết 11: Luyện tập về hình thoi

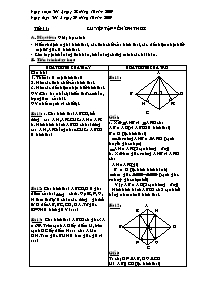
Ngaứy soaùn: Thửự 4 ngaứy 28 thaựng 10 naờm 2009
Ngaứy daùy: Thửự 5 ngaứy 29 thaựng 10 naờm 2009
 Tiết 11: luyện tập về Hình thoi
A. Mục tiêu: Giúp học sinh
- Hiểu rõ định nghĩa hình thoi, các tính chất của hình thoi, các dấu hiệu nhận biết một tứ giác là hình thoi.
- Rèn luyện khả năng tính toán, khả năng chứng minh các bài toán.
B. Tiến trình dạy học:
Hoạt động của thầy
Hoạt động của trò
Câu hỏi:
1. Thế nào là một hình thoi?
2. Nêu các tính chất của hình thoi.
3. Nêu các dấu hiệu nhận biết hình thoi.
GV: Cho hs nhắc lại kiến thức cơ bản, trọng tâm của bài.
GV nhấn mạnh và chốt lại.
Bài 1: a. Cho hình thoi ABCD, kẻ đường cao AH, AK. CMR: AH = AK
b. Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. CMR: ABCD là hình thoi	 
Bài 2: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân các đường góc kẻ từ O đến AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?
Bài 3: Cho hình thoi ABCD có góc <A = 600. Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì? vì sao?
 A
Bài 1:
 B O D
 H K
 C	
Giải:	
a. Xét AHB và AKD có:
AB = AD (vì ABCD là hình thoi)
B = D (t/c hình thoi) 
 vuông AHB = AKD (cạnh huyền góc nhọn)	 	 
AH = AK (2 cạnh tương ứng)	
b. Xét tam giác vuông AHB và AKD có: 
 AH = AK (gt) 
 B = D (t/c hình bình hành)
tam giác (cạnh góc vuông- góc nhọn kề)
Vậy AB = AD (2 cạnh tương ứng)
 Hình bình hành ABCD có 2 cạnh kề bằng nhau nên là hình thoi.
Bài 2: A
 E H
O
 B D
 F G
 C
Giải:	
Ta có; OF AB, OG CD	 
Mà AB // CD (t/c hình thoi)
	E, O, G thẳng hàng.	
Chứng minh tương tự ta có 3 điểm	
 F, O, H thẳng hàng.
- Điểm O thuộc tia phân giác của góc B
nên cách đều 2 cạnh của góc do đó: OE = OF
Tương tự ta cũng có:OF = OG, OG=OH
Vậy tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên là hình chữ nhật.
Bài 3:
Ta có: Tam giác ABD cân tai A
Và <A = 600 nên tam giác ABC là tam giác đều.
	AB = BD 	
góc <ABD = <D1 = 600 (t/c hình thoi)
Xét tam giác ABM và DBN có: 	
AB = BD (chứng minh trên)	 
Góc <A = <D2 (chứng minh trên) 
AM = DN (gt) 
ABM = (c.g.c)	
 BM = BN, <B1 = <B3
Ta lại có: góc, <B1 + <B2 = 600
	<B3 + <B2 = 600
Tam giác BMN cân có góc MBN = 600 nên là tam giác đều.