Giáo án tự chọn môn Toán Lớp 8 - Tiết 1: Ôn tập đơn thức. Đa thức - Phạm Minh Vũ

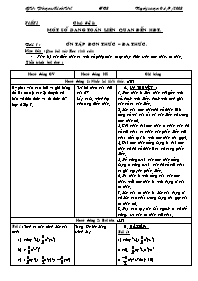
TiÕt1	Chủ đề 1:
MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN HĐT.
Bài 1:	 ÔN TẬP ĐƠN THỨC – ĐA THỨC.
Mục tiêu : Qua bài này Học sinh cần:
Nắm lại các kiến thức và một số phép toán được thực hiện trên đơn thức, đa thức.
 Tiến trình bài dạy : 
Hoạt động GV
Hoạt động HS
Ghi bảng
Hoạt động 1: Nhắc lại kiến thức. (10’)
Gv phát vấn câu hỏi và ghi bảng để Hs ôn tập các lý thuyết cơ bản về đơn thức và đa thức đã học ở lớp 7.
Trả lời theo câu hỏi của GV
Lấy ví dụ minh họa cho từng kiến thức.
LÝ THUYẾT : 
1. Đơn thức là biểu thức chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
2. Bậc của đơn thức(hệ số khác 0) là tổng số mũ của tất cả các biến có trong đơn thức đó.
3. Khi nhân hai đơn thức ta nhân các hệ số với nhau và nhân các phần biến với nhau (kết quả là một đơn thức thu gọn).
4. Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
5. Để cộng (trừ) các đơn thức đồng dạng ta cộng (trừ) các hệ số với nhau và giữ nguyên phần biến.
6. Đa thức là một tổng của các đơn thức, mỗi đơn thức là một hạng tử của đa thức.
7. Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
8. Dựa vào quy tắc dấu ngoặc ta có thể cộng, trừ các đa thức với nhau.
Hoạt động 2: Bài tập.(33’)
Bài 1: Tính và xác định bậc của tích:
(-2xy2z).(x2yz3)
(-u3v4)3
(xy2).( x2y)2.( yx2)
Từng Hs lên bảng trình bày
 B. BÀI TẬP:
Bài 1:
a) (-2xy2z).(x2yz3)
= (-2). .xy2z.x2yx3
= x3y3z4 (bậc 10)
b) (-u3v4)3
= u9v12 (bậc 21)
c) (xy2).( x2y)2.( yx2)
(BTVN)
Bài 2: Tính :
a) -3x4yz2 + x4yz2
b) ax2y3 - 2 x2y3 + b2 x2y3 (a,b:hằng số)
c) 3uv2 – ( uv2 +367 uv2 - uv2 ) +(uv2) + 367uv2
Hai Hs lên trình bày
Bài 2: Tính:
a) -3x4yz2 + x4yz2
 = (-3 +1) x4yz2
 = -2x4yz2
b) ax2y3 - 2 x2y3 + b2 x2y3
 = (a – 2 + b) x2y3
 = (a+b-2) x2y3
c) 3uv2 – ( uv2 +367 uv2 - uv2 ) + (uv2) + 367uv2 
(BTVN)
Bài 3: Tìm đa thức A biết:
a) A + (x2 + y2) = 5x2 + 3y2 - xy
b) A – (xy + x2 – y2) = x2 + y2
Một Hs trình bày.
Bài 3: Tìm đa thức A biết:
a) A + (x2 + y2) = 5x2 + 3y2 - xy
Þ A = (5x2 + 3y2 – xy) - (x2 + y2)
 = 5x2 + 3y2 – xy - x2 - y2
 = 4x2 + 2y2 – xy
b) A – (xy + x2 – y2) = x2 + y2
(BTVN)
Bài 4: Cho hai đa thức:
f(x) = x5- 3x2+ x3- 2x + 5
g(x) = x2- 3x + 1 + x2 – x4 +x5
Sắp xếp và tính theo hàng dọc:
f(x) + g(x)
f(x) – g(x).
Lưu ý: Khi sắp xếp, ta nhớ để trống các bậc bị khuyết.
Một Hs trình bày.
Bài 4: Sắp xếp và tính theo hàng dọc:
a) f(x) + g(x)
 f(x) = x5 +x3-3x2 - 2x+5
 + g(x) = x5-x4 + x2 -3x+1 
 f(x)+g(x) = 2x5-x4+x3-2x2-5x+6
b) f(x) – g(x).
(BTVN)
Hoạt động 4: Kết thúc bài học: (2’)
 +Về nhà :Xem lại lý thuyết và các bài tập đã làm.
 + Làm các bài tập còn lại.
 + Chuẩn bị bài sau: Phép nhân đa thức.