Giáo án môn Đại số 8 - Tiết 46: Luyện tập - Ngô Thanh Hữu

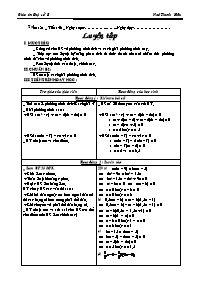
Tuần : 21 _ Tiết : 46 _ Ngày soạn:....Ngày dạy:
Luyện tập
I. MỤC TIÊU:
_ Củng cố cho HS về phương trình tích và cách giải phương trình này.
_ Tiếp tục rèn luyện kỹ năng phân tích đa thức thành nhân tử nhằm đưa phương trình đã cho về phương trình tích.
_ Rèn luyện tính cẩn thận , chính xác.
II. CHUẨN BỊ :	
HS ôn tập cách giải phương trình tích.
III. TIẾN TRÌNH DẠY HỌC :
Trợ giúp của giáo viên
Hoạt động của học sinh
Hoạt động 1 : Kiểm tra bài cũ
_ Thế nào là phương trình tích?Cách giải ?
_ Giải phương trình sau :
 + HS1 : (x2 - 4) + (x – 2)(3 – 2x) = 0
 + HS2 : x(2x – 7) – 4x + 14 = 0
_ GV nhận xét và cho điểm.
_ HS trả lời theo yêu cầu của GV.
 + HS1 : (x2 - 4) + (x – 2)(3 – 2x) = 0
 ĩ (x + 2)(x – 2) + (x – 2)(3 – 2x) = 0
 ĩ (x – 2)(-x + 5) = 0
 ĩ x = 2 hoặc x = 5
 + HS2 : x(2x – 7) – 4x + 14 = 0
 ĩ x(2x – 7) – 2 (2x – 7) = 0
 ĩ (2x – 7)(x – 2) = 0
 ĩ x = 2 và x = 3,5
Hoạt động 2 : Luyện tập
_ Làm BT 23 SGK.
 + Chia làm 4 nhóm.
 + Thảo luận khoảng 4 phút.
 + Gọi 4 HS lên bảng làm.
GV chú ý HS các vấn đề sau :
 + Khi bỏ dấu ngoặc mà bên ngoài dấu trừ thì các hạng tử bên trong phải đổi dấu.
 + Khi chuyển vế phải đổi dấu hạng tử.
_ GV nhận xét và sửa sai cho HS (có thể cho điểm nếu HS làm chính xác)
_ Làm BT 24 SGK.
 + Tương tự cho HS thảo luận nhóm khoảng 4 phút.
 + Gọi 4 HS lên bảng. 
 GV gợi ý HS áp dụng các HĐT để đưa các pt đã cho về dạng tích.
 + Câu a dùng hằng đẳng thức bình phương của một hiệu và hiệu hai bình phương.
 + Câu b dùng phương pháp nhóm hạng tử.
 + Câu c dùng hằng đẳng thức bình phương của một tổng và hiệu hai bình phương.
+ Câu d dùng phương tách hạng tử : -5x = x – 6x
_ GV nhận xét.
_ Làm BT 25 SGK.
* Đối với các pt này ta có thể :
- Chuyển tất cả các hạng tử về riêng vế trái.
- Dùng pp nhóm hạng tử để phân tích vế trái thành nhân tử à đưa về dạng pt tích.
* GV gọi HS lên bảng làm câu a
* Câu b: Nếu HS làm không được thì GV hướng dẫn HS cách giải.
* Dặn dò : 
Về nhà làm các BT còn lại và xem trước bài 5 SGK.
23) a) x(2x – 9) = 3x(x – 5) 
 2x2 – 9x = 3x2 – 15x
 3x2 – 15x – 2x2 + 9x = 0
 x2 – 6x = 0 x(x – 6) = 0 
 x = 0 hoặc x – 6 = 0
 x = 0 hoặc x = 6
b) 0,5x(x – 3) = (x – 3)(1,5x – 1)
 0,5x(x – 3) – (x – 3)(1,5x – 1) = 0
 (x – 3)(0,5x – 1,5x + 1) = 0
 (x – 3)(1 – x) = 0
 x – 3 = 0 hoặc 1 – x = 0
 x = 3 hoặc x = 1
c) 3x – 15 = 2x(x – 5)
 3(x – 5) – 2x(x – 5) = 0
 (x – 5)(3 – 2x) = 0
 x = 5 hoặc x = 1,5
d) 
24) a) (x2 – 2x + 1) – 4 = 0
 (x – 1)2 – 22 = 0 
 (x – 1 – 2)(x – 1 + 2) = 0
 (x – 3)(x +1) = 0 
 x = 3 hoặc x = -1
b) x2 – x = -2x + 2
 x2 – x + 2x – 2 = 0
 (x2 – x) + (2x – 2) = 0
 x(x – 1) + 2(x – 1) = 0
 (x – 1)(x + 2) = 0 
 x = 1 hoặc x = -2
c) 4x2 + 4x +1 = x2
 (4x2 + 4x + 1) – x2 = 0 
 (2x + 1)2 – x2 = 0 
 (2x + 1 – x)(2x+1 + x) = 0
 (x + 1)(3x + 1) = 0 
 x = -1 hoặc x = -1/3
d) x2 – 5x + 6 = 0 
 x2 + x – 6x + 6 = 0
 (x2 + x) – (6x – 6) = 0
 x(x – 1) – 6(x – 1) = 0
 (x – 1)(x – 6) = 0 
 x = 1 hoặc x = 6
25) a) 2x3 + 6x2 = x2 + 3x
 (2x3 + 6x2) – (x2 + 3x) = 0
 2x2(x + 3) – x(x + 3) = 0
 (x + 3)(2x2 – x) = 0 
 x(x + 3)(2x – 1) = 0
 x = 0 hoặc x = -3 hoặc x = ½
b) (3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
 (3x – 1)(x2 + 2) – (3x – 1)(7x – 10) = 0
 (3x – 1)[(x2 + 2) – (7x – 10)] = 0
 (3x – 1)( x2 + 2 – 7x + 10) = 0
 (3x – 1)( x2 – 7x + 12) = 0
 (3x – 1)[(x2 – 3x) – (4x – 12)] = 0
 (3x – 1)[(x(x – 3) – 4(x – 3)] = 0
 (3x – 1)(x – 3)(x – 4) = 0
 x = 1/3 ; x = 3 hoặc x = 4