Giáo án Hình học Lớp 8 - Tiết 21: Luyện tập - Lê Tấn Mạnh

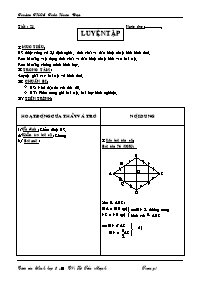
Tiết : 21 	Ngày dạy:.
LUYỆN TẬP
I/ MỤC TIÊU:
HS được củng cố lại định nghĩa, tính chất và dấu hiệu nhận biết hình thoi.
Rèn kĩ năng vận dụng tính chất và dấu hiệu nhận biết vào bài tập.
Rèn kĩ năng chứng minh hình học.
II/ TRỌNG TÂM:
-Luyện giải các bài tập về hình thoi.
III/ CHUẨN BỊ:
HS: Như dặn dò của tiết 20.
GV: Phim trong ghi bài tập, bài học kinh nghiệm.
IV/ TIẾN TRÌNH:
HOẠT ĐỘNG CỦA THẦY VÀ TRÒ
NỘI DUNG
1/ Oån định: Kiểm diện HS.
2/ Kiểm tra bài cũ: Không
3./ Bài mới:
GV đưa bài tập 134 lên màn hình.
Bài tập 134:(SBT)
a/ Cho gình thoi ABCD. Kẻ hai đường cao AH, AK
CMR: AH = AK
b/ Hình bình hành ABCD có hai đường cao AH; AK bằng nhau. CMR: ABCD là hình thoi.
GV cho HS hoạt động nhóm 
Nhóm 1, 2, 3: câu a.
Nhóm 4, 5, 6: câu b.
Thời gian 10 phút.
-GV đưa lên màn hình bài tập 139 (SBT)
Cho hình thoi ABCD có chu vi bằng 16 cm, đường cao AH bằng 2 cm. Tính các góc hình thoi.
GV gọi 1 HS lên bảng vẽ hình 
GV lưu ý: chu vi hình thoi bằng 16 cm cạnh hình thoi bằng 4 cm hS vẽ hình cho đúng.
GV hỏi: 
rAHD vuông tại H.
Muốn tính góc C thì ta cần tính góc nào?
HS: Góc DAH 
GV gợi ý vẽ thêm điểm E sao cho H là trung điểm AE rADE là tam giác đều.
 DAH = 600
 D = 300
GV: Hãy quan sát r đều ADE 
Ta thấy đường cao DC chia r đều ADE thành 2 tam giác vuông bằng nhau.
Vậy có thể nói r vuông ADH , r vuông DEH là nửa tam giác đều.
Vậy khi nào thì một tam giác vuông có thể kết luận là nửa tam giác đều.
HS phát biểu như bài học kinh nghiệm.
GV: Ta có thể xem bài học kinh nghiệm vừa rút ra như một tính chất và có thể vận dụng vào bài tập.
GV yêu cầu 1 HS vận dụng bài học kinh nghiệm chứng minh lại bài tập 139 bằng miệng.
5/ Dặn dò:
I/ Sửa bài tập cũ:
Bài tập 76 (SGK):
x
x
O
B
M
A
Q
D
P
C
N
MN là đường trung bình của rABC
Xét r ABC:
MA = MB (gt)
NC = NB (gt)
(1)
 MN // AC
 MN = AC 
Chứng minh tương tự ta có:
(2)
PQ // AC 
PQ = AC 
(1)(2) MN // PQ
 MN = PQ
Vậy MNPQ là hình bình hành. (3)
Gọi O là giao điểm của AC và BD
ACBD
xét rABD:
MQ là đường trung bình của rABD.
MA =MB (gt)
QA = QD (gt)
 MQ // BD 
Mà BD AC (cmt)
MQ MN
Nên MQ AC
 AC // MN 
QMN = 900 (4)
(3)(4) MNPQ là hình chữ nhật .
II/ Bài mới: 
Bài tập 134 (SBT):
D
H
C
K
B
A
a/ 
Hình thoi ABCD 
AHDC ; AK CB
AH = AK
GT
KL
Xét r vuông ADH và r vuông ABK:
AD = AB ( ABCD là hình thoi).
D = B ( ABCD là hình thoi)
Vậy r vuông ADH = r vuông ABK
( cạnh huyền – góc nhọn).
D
H
C
K
B
A
1
2
AH = AK.
b/ 
Hình bình hành ABCD
AHDC
AKBC
AH = AK
 ABCD là hình thoi
GT
KL
rADH có:
 H + D + A1 = 1800
A1 = A2
rABK có:
 K + B + A2 = 1800
 H = K ( cùng bằng 900)
 D = B ( ABCD là hbh).
rADH = rABK ( g- c- g)
 AD = AB
hình bình hành ABCD có AD = AB
Nên ABCD là hình thoi.
Bài tập 139 (SBT):
A
B
C
H
E
D
2
Hình thoi ABCD
AB + BC + CD + DA = 16 cm 
AHDC ; AH = 2 cm.
D = ? ; B = ? ; A= ? ; C= ?
GT
KL
Trên tia AH lấy E sao cho 
H là trung điểm AE
rADH =rEDH (g-c-g)
 AD = DE
Mà : AD = 2 cm nên DE = 2 cm 
AE = 2AH = 2.2 = 4 cm
Vậy AD = DE = EA ( cùng bằng 2 cm).
Suy ra rADE đều.
DAH = 600
rAHD vuông tại H
DAH + D = 900
600 + D = 900
 D = 300
Nên B = 300 ( vì D = B)
Ta có:
D + DAB = 1800 ( trong cùng phía do AB// DC)
300 + ADB = 1800 ADB = 1500
Nên DCA = 1500 ( vì ADB = DCA)
III/ Bài học kinh nghiệm:
Tam giác vuông có một góc bằng 300 hoặc 600 là nữa tam giác đều.
Khi đó ta có cạnh góc vuông đối diện góc 300 bằng nữa cạnh huyền.
Tam giác vuông có cạnh huyền bằng hai lần cạnh góc vuông là nửa tam giác đều. Khi đó ta có góc đối diện với cạnh góc vuông đó bằng 300.
-Học thuộc bài học kinh nghiệm.
-Làm bài tập : 139, 141 (SBT).
-Xem lại:
+Tính chất hình chữ nhật .
+ Tính chất hình thoi.
V/ RÚT KINH NGHIỆM: