Giáo án Hình học Lớp 8 - Tiết 1 đến 22 - Lê Kim Thương
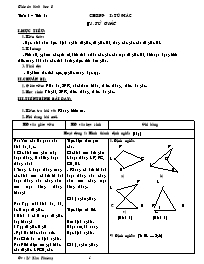
Gv: Yêu cầu Hs quan sát hình 1a, b, c.
? Các hình trên gồm mầy đoạn thẳng, là những đoạn thẳng nào?
? Trong 4 đoạn thẳng trong các hình trên có bất kì hai đoạn thẳng nào cùng nằm trên một đường thẳng không?
Gv: Vậy mỗi hình 1a, 1b, 1c là một tứ giác.
? Hình 2 có là một tứ giác hay không?
? Vậy tứ giác là gì?
- Gọi Hs khác nhân xét.
Gv: Chốt đưa ra định nghĩa.
Gv: Giới thiệu tên gọi khác của tứ giác ABCD, các đỉnh, các cạnh của tứ giác ABCD.
Gv: Yêu cầu Hs thực hiện ?1( Tr 64 – Sgk).
Gv: Tứ giác ABCD trên hình 1a được gọi là tứ giác lồi.
? Vậy thế nào là tứ giác lồi?
Gv: Đưa chú ý.
Gv: Cho Hs nghiên cứu làm ?2
- Yêu cầu Hs thực hiện trả lời câu hỏi của bài ?2.
- Gọi Hs nhận xét, bổ xung đáp án của bạn.
Gv; Chốt, bổ xung, đáp án
Gv: Thực hiện khắc sâu kiến thức cho Hs Thực hiện theo yêu cầu.
Các hình trên đều gồm 4 đoạn thẳng AB, BC, CD, DA
- Không có bất kì hai đoạn thẳng nào cùng nằm trên cùng một đường thẳng.
Chú ý nghe giảng
Thực hiện trả lời.
Nêu định nghĩa.
Nhận xet, bổ xung
Đọc định nghĩa.
Chú ý, nghe giảng
Suy nghĩ thực hiện làm ?1
Chú ý nghe giảng.
Nêu định nghĩa.
Đọc chú ý Sgk.
Thực hiên làm bài.
Lần lượt thực hiện câu trả lời.
Thựchiện theo yêu cầu.
Chú ý, sửa sai và ghi bài.
Chú ý nghe giảng.
Tuaàn 1 – Tieỏt 1: Chương I: Tứ Giác Đ1. Tứ giác I. Mục tiêu: 1. Kiến thức: - Học sinh nắm được định nghĩa tứ giác, tứ giác lồi, tổng các góc của tứ giác lồi. 2. Kĩ năng: - Biết vẽ, gọi tên các yếu tố, biết tính số đo các góc của một tứ giác lồi, biết vận dụng kiến thức trong bài vào các tình huống thực tiễn đơn giản. 3. Thái độ: - Nghiêm túc tích cực, tự giác trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, sách tham khảo, thước thẳng, thước đo góc. 2. Học sinh: Vở ghi, SGK, thước thẳng, thước đo góc. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: Không kiểm tra. 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Hình thành định nghĩa (20p) Gv: Yêu cầu Hs quan sát hình 1a, b, c. ? Các hình trên gồm mầy đoạn thẳng, là những đoạn thẳng nào? ? Trong 4 đoạn thẳng trong các hình trên có bất kì hai đoạn thẳng nào cùng nằm trên một đường thẳng không? Gv: Vậy mỗi hình 1a, 1b, 1c là một tứ giác. ? Hình 2 có là một tứ giác hay không? ? Vậy tứ giác là gì? - Gọi Hs khác nhân xét. Gv: Chốt đưa ra định nghĩa. Gv: Giới thiệu tên gọi khác của tứ giác ABCD, các đỉnh, các cạnh của tứ giác ABCD. Gv: Yêu cầu Hs thực hiện ?1( Tr 64 – Sgk). Gv: Tứ giác ABCD trên hình 1a được gọi là tứ giác lồi. ? Vậy thế nào là tứ giác lồi? Gv: Đưa chú ý. Gv: Cho Hs nghiên cứu làm ?2 - Yêu cầu Hs thực hiện trả lời câu hỏi của bài ?2. - Gọi Hs nhận xét, bổ xung đáp án của bạn. Gv; Chốt, bổ xung, đáp án Gv: Thực hiện khắc sâu kiến thức cho Hs Thực hiện theo yêu cầu. Các hình trên đều gồm 4 đoạn thẳng AB, BC, CD, DA - Không có bất kì hai đoạn thẳng nào cùng nằm trên cùng một đường thẳng. Chú ý nghe giảng Thực hiện trả lời. Nêu định nghĩa. Nhận xet, bổ xung Đọc định nghĩa. Chú ý, nghe giảng Suy nghĩ thực hiện làm ?1 Chú ý nghe giảng. Nêu định nghĩa. Đọc chú ý Sgk. Thực hiên làm bài. Lần lượt thực hiện câu trả lời. Thựchiện theo yêu cầu. Chú ý, sửa sai và ghi bài. Chú ý nghe giảng. 1. Định nghĩa. B B A C C A D D a) b) B A A C D B D c) C (Hình 1) (Hình 2) */ Định nghĩa: (Tr 64 – Sgk) - Tứ giác ABCD còn được gọi tên là tứ giác BCDA, BADC, ADCB,. Các điểm A, B, C, D gọi là các đỉnh. Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh. ?1 ( Tr 64 – Sgk). Đáp án: Tứ giác ABCD ở hình 1a. +) Tứ giác ABCD trên hình 1a gọi là tứ giác lồi. */ Định nghĩa: ( Tr 65 – Sgk). */ Chú ý: Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi. ?2 (Tr 65 – Sgk). Hình3 Đáp án: a) B và C, C và D, D và A. b) BD. c) BC và CD, CD và DA, DA và AB. - Hai cạnh đối nhau: AB và CD, AD và BC. d) Góc: , , , . - Hai góc đối nhau: và ; và e) Điểm nằm trong tứ giác: M, P - Điểm nằm ngoài tứ giác: N, Q. Hoạt động 2: Tổng các góc của một tứ giác (10p) Gv: Yêu cầu Hs thực hiện làm ?3. HD: Muốn tính tổng 4 góc của tứ giác ABCD ta nối AC hoăc BD toạ thành 2 tam giác rồi dựa vào định lí về tổng 3 góc trong 1 tam giác tính. Gv: Gọi Hs nhận xét, bổ xung. ? Em hãy phát biểu định lí về tổng các góc của một tứ giác? Gv: Chốt đưa ra nội dung định lí. 1 Hs lên bảng làm bài. 1 Hs lên bảng làm bài. Thực hiện theo yêu cầu. Thực hiện theo yêu cầu. Đọc bài và ghi bài. 2. Tổng các góc của một tứ giác. ?3 (Tr 65 – Sgk). Đáp án: a) rABC có: + + = 1800 b) Tứ giác ABCD. B C D Giải: Nối A vói C ta được hai tam giác ABC và ADC - Theo định lí tổng 3 góc trong 1 tam giác ta có:+ + = 1800 (1) + + = 1800 (2) - Từ (1) và (2) ta có: (+ )+ +(+ )+ = + + + = 3600 */ Định lí: Tổng các góc của một tứ giác bằng 3600 Hoạt động 3: Bài tập vận dụng (10p) Gv: Gọi 3 Hs lên bảng làm bài 1 HD: Ta áp dụng định lí về tổng các góc của một tứ giác để làm. - Gọi Hs nhận xét, bổ xung. Gv: Chốt, đáp án. Hs1,2: làm hình 5 Hs3: làm hình 6 Thực hiện nhân xet, bổ xung. */ Bài tập 1 (Tr 66 – Sgk). Đáp án: Hình 5: a) x = 600 ; b) x = 900 c) x = 1150 ; d) x = 750 Hình 6: a) x = (3600 – 650- 950) : 2 = 1000 b) x = 3600 : 10 = 360 3. Củng cố - Nhắc lại định nghĩa tứ giác, tứ giác lồi, định lí tổng các góc của một tứ giác. 4. Hướng dẫn học sinh tự học ở nhà - Về nhà học bài và làm các bài tập 2, 3, 4, 5 ( Tr 66, 67 – Sgk). - Đọc “ Có thể em chưa biết” (Tr 67 – Sgk). - Đọc và nghiên cứu trước bài: Hình thang. * Rỳt kinh nghiệm : Tieỏt 2: Đ2. hình thang I. Mục tiêu: 1. Kiến thức: - Học sinh nắm được định nghĩa hình thang, hình thang vuông, các yếu tố của hình thang. Biết cách chứng minh một tứ giác là hình thang, hình thang vuông. 2. Kĩ năng: - Biết vẽ hình thang, hình thang vuông. Biết tính số đo góc của hình thang, hình thang vuông. - Biết sử dụng dụng cụ để kiểm tra một tứ giác là hình thang. - Biết nhận dạng hình thang một cách linh hoạt ở những vị trí khác nhau ( hai đáy nằm ngang, hai đáy không nằm ngang) và ở các dạng đặc biệt ( hai cạnh bên song song, hai cạnh đáy bằng nhau). 3. Thái độ: - Nghiêm túc, tích cực, tự giác, cẩn thận trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, sách tham khảo, thước thẳng, thước đo góc, êke. 2. Học sinh: Vở ghi, SGK, thước thẳng, thước đo góc, êke. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: (5p) Nêu định nghĩa tứ giác? Làm bài tập 2a,b. 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Hình thành định nghĩa Gv: Đưa hình 13. Yêu cầu Hs nhận xét về hai cạnh đối AB và CD. Gv: Chốt, đưa nhận xét. ? Vậy hình thang là gì? Gv: Chốt, đưa định nghĩa. Gv: Đưa hình 14. giới thiệu các yếu tố của hình thang. +) Hình thang ABCD có: AB//CD. - AB, CD gọi là các đáy của hình thang. - AD, BC gọi là các cạnh bên. - AH gọi là đường cao của hình thang ABCD. Gv: Yêu cầu Hs thực hiện làm ?1. - Gọi Hs nêu câu trả lời. - Gọi Hs nhận xét, bổ xung. Gv: Chốt, đáp án. Gv: Yêu cầu Hs thực hiện làm ?2. HD: Từ hình vẽ ta kẻ đường chéo AC vận dụng định nghĩa hình thang và các trương hợp bằng nhau của tam giác để chúng minh. - Gọi 2 Hs lên bảng làm. - Gọi Hs nhận xét, bổ xung bài làm của bạn. Gv: Chốt, đáp án. ? Qua ?2 em cho biết: - Môt hình thang có hai cạnh bên // ( một hình thang có hai cạnh đáy bằng nhau) thì có đặc điểm gì? Gv: Chốt, đưa ra nhận xét Thực hiện nhận xét theo yêu cầu. Chú ý, ghi bài. Nêu đinh nghĩa. Chú ý, ghi bài. Quan sát hinh 14 Chú ý, nghe giảng và ghi bài. Suy nghĩ và làm bài. Nêu đáp án. Nhận xét, bổ xung Suy nghĩ làm bài. Chú ý làm bài theo hướng dẫn. Thưc hiện yêu cầu Nhận xet, bổ xung Suy nghi và nêu nhận xét. Đọc nhân xét Sgk. 1. Định nghĩa. - Hình 13 B A C D - Tứ giác ABCD có AB // CD là mọt hình thang */ Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song. Hình 14 - ở hình thang ABCD có AB // CD. - Các đoạn thẳng AB, CD gọi là các cạnh đáy (hoặc đáy). - Các đoạn thẳng AD và BC gọi là các cạnh bên. - Trong hình thang mà hai đáy không bằng nhau, người ta còn phân biệt đáy lớn và đáy nhỏ. -AH gọi là đường cao của hình thang. ?1 (Tr 69 – Sgk). Đáp án: a) Các tứ giác ABCD,GHEF là hình thang. Tứ giác IMLN không phải là hình thang. b) Hai góc kề một cạnh bên của hình thang thì bù nhau( hai góc trong cùng phía tạo bởi hai đường thẳng song song với một cát tuyến). ?2. (Tr70 – Sgk). Đáp án: - Kẻ đường chéo AC ta được hình 17, 17 tương đương như sau: Hình 16 Hình 17 a)Vì ABCD là hình thang +) AB//CD => = ( So le trong) +) AD//BC => = (so le trong) Do đó: rABC = rADC (g.c.g) => AD = BC, AB = CD. b) AB//CD => = (so le trong) Do đó: rABC = rADC (c.g.c) => AD = BC, = Do đó: AD//BC. */ Nhận xét: (Tr 70 – Sgk). Hoạt động 2: Hình thang vuông Gv: Đưa hình 18 và giới thiệu về hình thang vuông theo Sgk. ? Thế nào là hình thang vuông? Gv: Chốt, đưa định nghĩa. Chú ý nghe giang kết hợp đọc Sgk. Thực hiện trả lời. Đọc và ghi bài. 2. Hình thang vuông. Hinh 18, hình thang A B ABCD có AB//CD, = 900, khi đó: = 900. Ta goi tứ D C giác ABCD là hình thang vuông. */ Định nghĩa: Hình thang vuông là hình thang có một góc vuông. Hoạt động 3: Bài tập vận dụng Gv: Giới thiệu cách dùng thước và êke để kiểm tra hai đường thẳng //. Yêu cầu Hs làm bài tập 6 Gv: Yêu cầu cả lớp làm bài 7. - Gọi Hs lên chữa bài tâp. Gv: Nhận xét, đáp án Chú ý nghe giảng. Lên bảng thực hành làm bai 6 Cả lớp làm bài tâp 3 Hs lên bảng. Chú ý, ghi bài. */ Bài 6 (tr 70 – Sgk) Đáp án: - Hình 20(a, c) là hình thang. */ Bài 7 ( Tr 71- Sgk). Đáp án: a) x = 1000 ; y = 1400 b) x = 700 ; y = 500 c) x = 900 ; y = 1150 3. Củng cố ( - Hệ thống lại toàn bộ kiến thức cơ bản của bài. 4. Hướng dẫn học sinh tự học ở nhà - Về nhà học bài, làm bài tập 8, 9, 10 (Tr 71 – Sgk). Đọc trước bài: Hình thang cân. * Rỳt kinh nghiệm : Tuaàn 2 – Tieỏt 3: Đ3. hình thang cân I. Mục tiêu: 1. Kiến thức: - Học sinh nắm được định nghĩa, các tính chất, các dấu hiệu nhận biết hình thang cân. 2. Kĩ năng: - Biết vẽ hình thang cân, biết vận dụng kiến thức đã học vào tính toán, chứng minh, biết chứng minh một tứ giác là hình thang cân. - Rèn luyện cho học sinh tính chính xác và cách lập luận chứng minh hình học. 3. Thái độ: - Nghiêm túc, tích cực, tự giác, cẩn thận trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, sách tham khảo, thước thẳng, thước đo góc. 2. Học sinh: Vở ghi, SGK, thước thẳng, thước đo góc. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: (5p). Phát biểu nhận xét (Tr 70 – Sgk). Làm bài tập 8 ( Tr71- Sgk). 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Hình thành định nghĩa Gv: Đưa hình 23. Yêu cầu Hs thực hiện ?1. - Gọi Hs nêu đáp án. Gv: Giới thiệu hình thang ABCD ở trên gọi là hình thang cân. ? Thế nào là hình thang cân? Gv: Đưa định nghĩa. Gv: Phân tích định nghĩa. Gv: Đưa ra chú ý. Gv: Yêu cầu Hs vận dụng thực hiện làm ?2. - Gọi Hs lần lượt trả lời các câu a,b,c. - Gọi Hs nhận xet. Gv: Nhận xét, đáp án. Quan sát hình 23 và thực hiên làm bài ?1. Hình thang ABCD có = . Chú ý, nghe giảng Thực hiện trả lời. Đọc và ghi bài. Chú ý, ghi bài. Đọc chú ý Sgk. Thực hiện làm bài ?2. Trả lời theo yêu cầu. Nhận xet, bổ xung Chú ý, ghi bài. 1. Định nghĩa. ?1.(Tr 72 – Sgk) A B - Hình thang có hai góc ở đáy bằng nhau. D C */ Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. - Tứ giác ABCD là hình thang cân có dáy AB, CD ⇔ AB//CD, = hoặc = . */ Chú ý: (Tr 72 – Sgk). ?2. (Tr72 – Sgk). Đáp án: a) Các hình thang cân: ABDC, IKMN, PQST. b) Các góc còn lại: = 1000, = 1100 = 700, = 900. c) Hai góc đối của hình thang cân thì bù nhau. Hoạt động 2: Các tính chất của hình thang cân Gv: Đưa định lí. HD: Khi Cm định lí 1 ta xét 2 trường hợp: 1) AD cắt BC tại O đáy AB < DC. HD: Sử dụng Tam giác cân và phép trừ hai cạnh. 2) AD//BC. HD: Sử d ... đường phân giác. ị AC ^ BD, BD là phân giác . +) Tường tự: chứng minh AC, CA, DB là phân giác . */ Để vẽ hình thoi ta vẽ hai đoạn thẳng vuông góc với nhau tại trung điểm mỗi đường va nối các mút lại với nhau. Hoạt động 3: Dấu hiệu nhận biết. Gv: Yêu cầu Hs từ định nghĩa và tính chất đưa ra dấu hiệu nhận biết. Gv: Chốt, đưa ra dấu hiệu nhận biết. Gv: Cho Hs làm ?3. HD: Làm tương tự chứng minh Định lí a. Đưa ra các dấu hiệu nhận biết. Chú ý, đọc bài. Làm bài. 3. Dấu hiệu nhận biết. */ Dấu hiệu nhận biết: (Tr 105 – Sgk). ?3. (Tr 104 – Sgk). C/m tương tự ý a của định lí. 3. Củng cố. - Nhắc lại: +) Định nghĩa, tính chất, dấu hiệu nhận biêt hình thoi. 4. Hướng dẫn học sinh tự học ở nhà. - Về nhà học bài. Làm bài tập 73, 74(Tr 106 – Sgk). - Xem trước các bài tập 75 -> 78 (Tr 106 – Sgk) giờ sau Luyện tập. */ Hướng dẫn: Bài 75 (Tr 106 – Sgk). +) Ta chứng minh 4 tam giác vuông AEH, BEF, CGF, DGH băng nhau. * Rỳt kinh nghiệm : Tiết 20 Luyện tập ( Hỡnh Thoi ) I. Mục tiêu: 1. Kiến thức: - Củng cố, khắc sâu kiến thức về hình thoi cho Hs. 2. Kĩ năng: - Hs biết vẽ hình thoi, biết chứng minh một tứ giác là hình thoi. - Hs biết vận dụng các kiến thức về hình thoi trong tính toán, chứng minh và trong các bài toán thực tế. 3. Thái độ: Nghiêm túc, tích cực, tự giác trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, SBT, thước thẳng, êke. 2. Học sinh: Vở ghi, SGK, thước thẳng, êke. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: Nêu dấu hiệu nhận biết hình thoi. Chứng minh dấu hiệu 2. 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Luyện tập. Gv: Cho Hs làm bài tập 75 - Sgk. - Gọi Hs vẽ hình và ghi GT, KL. - Gọi Hs lên bảng làm bài. - Gọi Hs nhận xét câu trả lời của bạn. Gv: Nhận xét, bổ xung và đáp án. Gv: Cho Hs làm bài 76. HD: Để chứng minh EFGH là hình chữ nhật trước tiên ta phải chứng minh EFGH là hình bình hành, chứng minh hình bình hành EFGH có 1 góc vuông. - Gọi Hs lên bảng trình bày lời giải. - Gọi Hs nhận xét. Gv: Nhận xét, bổ xung, đáp án. Làm bài. Thực hiện yêu cầu 1 Hs lên bảng làm bài. Thực hiện nhận xét, bổ xung. Thực hiện làm bài Chú ý làm bài theo hướng dẫn. 1 Hs lên bảng làm bài. Nhận xét, bổ xung 1. Bài 75: (Tr 106 – Sgk). GT ABCD là hình chữ nhật, E AB, F BC, G CD, H DA AE = EB, BF = FC, CG = GD AD = HA KL EFGH là hình thoi. Chứng minh: Xet ∆AEH và ∆BEF có: AE = EB, AH = BF (gt) Do đó: ∆AEH = ∆BEF (c.g.c) ị EH = EF (1). Tương tự, ta chứng minh được: EF = FG, FG = GH, GH = HE (2) Từ (1) và (2), ta có: EFGH là hình thoi. 2. Bài 76: (Tr 103 – Sgk). GT ABCD là hình thoi, E AB, AE = EB; F BC, BF = FC G CD, CG = GD; H DA, DH = HA. KL EFGH là hình chữ nhật. Chứng minh: EF là đường trung bình của ∆ABC ị EF//AC (1) GH là đường trung bình của ∆ADC ị GH//AC (2) Từ (1), (2) suy ra: EF//GH. Tương tự ta có: FG//HE Do đó: EFGH là hình bình hành. Mặt khác: EF//AC, BD ^ AC ị BD ^ EF HE // BD, EF ^ BD ị EF ^ HE Vậy nên EFGH là hình chữ nhật theo (dấu hiệu 3). 3. Củng cố. - Hệ thống lại kiến thức cơ bản toàn bài. 4. Hướng dẫn học sinh tự học ở nhà. - Về nhà học bài, xem lại các bài tập đã chữa. - Đọc và nghiên cứu trước bài: Hình vuông (Tr 107 – Sgk). * Rỳt kinh nghiệm : Tuần 11 – Tiết 21 Đ12. hình vuông. I. Mục tiêu: 1. Kiến thức: - Hs nắm được định nghĩa, tính chất của hình vuông, các dấu hiệu nhận biết một tứ giác là hình vuông. Thấy được hình vuông là một dạng đặc biệt của hình chữ nhật, hình thoi. 2. Kĩ năng: - Hs biết vẽ hình vuông, biết chứng minh một tứ giác là hình vuông. - Hs biết vận dụng các kiến thức về hình vuông trong tính toán, chứng minh và trong các bài toán thực tế. 3. Thái độ: - Nghiêm túc, tích cực, tự giác trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, sách tham khảo, thước thẳng, êke. 2. Học sinh: Vở ghi, SGK, thước thẳng, êke. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: Nêu định nghĩa hình chữ nhật, hình thoi? 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Định nghĩa. Gv: Vẽ hình 104. ? Tứ giác ở hình 104 có gì đặc biệt? Gv: Giới thiệu tứ giác ở hình 104 là hình vuông. ? Hình vuông là gì? ? Vậy hình vuông có phải là một hình chữ nhật, hình thoi không? Vẽ vào vở. Thực hiện trả lời. Chú ý, ghi bài. Suy nghĩ trả lời. Thực hiện làm bài theo hướng dẫn. Nêu hướng c/m Trả lời. 1. Định nghĩa. Hình 104 - Tứ giác ABCD có: và AB = BC = CD = DA là một hình vuông. */ Định nghĩa: (Tr 104 – Sgk). - Tứ giác ABCD là hình vuông Û AB = BC = CD = DA */ Hình vuông cũng là một hình chữ nhật, cũng là hình thoi. Hoạt động 2: Tính chất. Gv: Giới thiệu hình thoi có đầy đủ các tính chất của hình bình hành. ? Nêu các tính chất của hình thoi? Gv: Cho Hs thực hiện ?1. - Gọi Hs thực hiện trả lời. - Gọi Hs nhận xét, bổ xung. Gv: Nhận xét, bổ xung và đáp án. Gv: Để vẽ một hình vuông đơn giản và chính xác nhất ta làm ntn? Gv: Để vẽ hình vuông ta vẽ hai đoạn thẳng bằng nhau, vuông góc, với nhau tại trung điểm mỗi đường và nối các đầu mút với nhau. Chú ý, nghe giảng Thực hiện yêu cầu Thực hiện làm bài Làm bài theo yêu cầu. Nhận xét, bổ xung. Thực hiện yêu cầu 2. Tính chất. */ Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi ?1. (Tr 107 – Sgk). - Hai đường chéo của hình vuông: +) Vuông góc với nhau. +) Bằng nhau. +) Cắt nhau tai trung diểm mỗi đường +) Là đường phân giác của các góc tương ứng. */ Để vẽ hình vuông ta vẽ hai đoạn thẳng bằng nhau và vuông góc với nhau tại trung điểm mỗi đường và nối các mút lại với nhau. Hoạt động 3: Dấu hiệu nhận biết. Gv: Yêu cầu Hs từ định nghĩa và tính chất đưa ra dấu hiệu nhận biết. Gv: Chốt, đưa ra dấu hiệu nhận biết. ? Vậy một tứ giác vừa là hình thoi vừa là hình chữ nhật có phải là hình vuông không? Gv: Cho Hs vận dụng là bài ?2. Đưa ra các dấu hiệu nhận biết. Chú ý, đọc bài. Trả lời: Là hình vuông. Thực hiện làm bài. 3. Dấu hiệu nhận biết. */ Dấu hiệu nhận biết: (Tr 105 – Sgk). */ Chú ý: (Tr 107 – Sgk). ?2. (Tr 108 – Sgk). H105a là hình vuông (D.hiệu 1). H105c là hình vuông (D.hiệu 2). H105d là hình vuông (D.hiệu 4). Hoạt động 4: Luyện tập. Gv: Cho Hs vận dụng làm bài 81. - Gọi Hs trình bày lời giải. - Gọi Hs nhận xét,bổ xung. Gv: Nhận xét, bổ xung và đáp án. Thực hiện làm bài. Thực hiện yêu cầu Nhận xét, bổ xung */Bài 81: (Tr 108 – Sgk). - Tứ giác AEDF Là hình vuông. GT: - AEDF là hình bình hành (Đ/n). - Hình bình hành AEDF có AD là phân giác của nên là hình thoi. - Hình thoi AEDF có nên là hình vuông (D. hiệu 4). 3. Củng cố. - Nhắc lại: +) Định nghĩa, tính chất, dấu hiệu nhận biết hình vuông. 4. Hướng dẫn học sinh tự học ở nhà. - Về nhà học bài. Làm bài tập 79, 80, 82(Tr 108 – Sgk). - Xem trước các bài tập 83 -> 86 (Tr 109 – Sgk) giờ sau Luyện tập. */ Hướng dẫn: Bài 82 (Tr 106 – Sgk). HD: +) Chứng minh: ∆AHE = ∆BEF = ∆CFG = ∆DGH ị HE = EF = FG = GH. +) Sau đó chứng minh: +) Vậy EFGH là hình vuông (Dấu hiệu 4). * Rỳt kinh nghiệm : Tiết 22: Luyện tập ( Hỡnh vuụng ) I. Mục tiêu: 1. Kiến thức: - Củng cố, khắc sâu kiến thức về hình vuông cho Hs. 2. Kĩ năng: - Rèn cho Hs kĩ năng vẽ hình, chứng minh các đoạn thẳng bằng nhau. - Hs biết vận dụng các kiến thức về hình vuông vào tính toán, chứng minh và trong các bài toán thực tế. 3. Thái độ: Nghiêm túc, tích cực, tự giác trong học tập. II. Chuẩn bị: 1. Giáo viên: Giáo án, SGK, SBT, thước thẳng, êke. 2. Học sinh: Vở ghi, SGK, thước thẳng, êke. III. Tiến trình bài dạy: 1. Kiểm tra bài cũ: Nêu dấu hiệu nhận biết hình vuông ? Chứng minh dấu hiêu 2? 2. Nội dung bài mới. HĐ của giáo viên HĐ của học sinh Ghi bảng Hoạt động 1: Luyện tập. GV: Xem caực caõu sau ủuựng hay sai? Neỏu sai haừy neõu moọt phaàn vớ duù? a) Tửự giaực coự 2 ủửụứng cheựo vuoõng goực vụựi nhau laứ hỡnh thoi ? b) Tửự giaực coự 2 ủửụứng cheựo vuoõng goực vụựi nhau taùi trung ủieồm cuỷa moói ủửụứng laứ hỡnh thoi . c) Hỡnh thoi laứ tửự giaực coự taỏt caỷ caực caùnh baống nhau. d) Hỡnh chửừ nhaọt coự 2 ủửụứng cheựo baống nhau laứ hỡnh thoi. e) Hỡnh chửừ nhaọt coự hai ủửụứng cheựo vuoõng goực vụựi nhau laứ hỡnh vuoõng. Gv: Cho Hs laứm baứi taọp 84 - Sgk. -Cho D chaùy treõn caùnh BC ụỷ vũ trớ naứo cuỷa D thỡ tửự giaực ADEF laứ hỡnh thoi? Vỡ sao? -Neỏu cho Â= 90o thỡ tửứ giaực AFDE laứ hỡnh gỡ ? -Keỏt hụùp caõu hoỷi treõn, ủeồ coự AFDE laứ hỡnh vuoõng caàn coự theõm giaỷ thuyeỏt gỡ ? Gv: Cho Hs leõn baỷng laứm baứi 85. HD: a) Chửựng minh ADEF laứ hỡnh chửừ nhaọt, hỡnh chửừ nhaọt coự AE = AD neõn laứ hỡnh vuoõng. b) Cm ENFM laứ hỡnh thoi vỡ neõn ENFM laứ hỡnh vuoõng. - Goùi Hs nhaọn xeựt, boồ xung. Gv: Nhaọn xeựt, boồ sung vaứ ủaựp aựn. HS:caõu naứy sai. vớ duù: HS:ủaõy laứ moọt caõu ủuựng . HS: Caõu naứy ủuựng (theo ủũnh nghúa) HS:caõu naứy sai (moùi hỡnh chửừ nhaọt ủeàu coự 2 ủửụứng cheựo baống nhau) HS:caõu naứy ủuựng (D hiệu 2). - Moọt Hs leõn baỷng laứm baứi. Dửụựi lụựp laứm vaứo vụỷ. Traỷ lụứi theo yeõu caàu. Traỷ lụứi: Hỡnh vuoõng. 1 Hs leõn baỷng veừ hỡnh vieỏt GT, KL vaứ laứm baứi. Chuự yự laứm baứi theo hửụựng daón. Nhaọn xeựt, boồ sung. Chuự yự, sửỷa sai vaứ ghi vụỷ. 1. Baứi taọp: (Tr 109 – Sgk). Caực caõu sau ủaõy ủuựng hay sai ? a) Tửự giaực coự 2 ủửụứng cheựo vuoõng goực vụựi nhau laứ hỡnh thoi ? b) Tửự giaực coự 2 ủửụứng cheựo vuoõng goực vụựi nhau taùi trung ủieồm cuỷa moói ủửụứng laứ hỡnh thoi . c) Hỡnh thoi laứ tửự giaực coự taỏt caỷ caực caùnh baống nhau. d) Hỡnh chửừ nhaọt coự 2 ủửụứng cheựo baống nhau laứ hỡnh thoi. e) Hỡnh chửừ nhaọt coự hai ủửụứng cheựo vuoõng goực vụựi nhau laứ hỡnh vuoõng. 2. Baứi taọp 84: (Tr 109 – Sgk). a) AEDF laứ hỡnh bỡnh haứnh Vỡ AF // DE, AE // DF (gt) b) Neỏu theõm AD laứ phaõn giaực cuỷa BAC thỡ AEDF laứ hỡnh thoi. c) Neỏu = 900 thỡ hỡnh bỡnh haứnh AEDF laứ hỡnh chửừ nhaọt. d) Neỏu = 900 vaứ neỏu AD laứ phaõn giaực cuỷa BAC thỡ ta chửựng minh ủửụùc AEDF laứ hỡnh vuoõng. 3. Baứi 85: (Tr 109 – Sgk). GT ABCD laứ hỡnh chửừ nhaọt, AB = 2AD, E AB, AE = EB. F CD, CF = FD AF DE = M; BF CE = N. KL a) ADFE laứ hỡnh gỡ? Vỡ sao? b) EMFN laứ hỡnh gỡ? Vỡ sao? a) Theo GT: AB = 2 AD vaứ E, F laứ trung ủieồm AB, CD neõn: AE= AD= DF= EF Vaứ AÂ = 900 . Suy ra AEFD laứ hỡnh vuoõng. b)EMFN laứ hỡnh thoi vỡ: EM= MF= FN= NE Vaứ = 900 ( chửựng minh treõn). ị EMFN laứ hỡnh vuoõng. 3. Cuỷng coỏ: - Nhaộc laùi: ẹũnh nghúa, tớnh chaỏt, daỏu hieọu nhaọn bieỏt hỡnh vuoõng. 4. Hửụựng daón veà nhaứ. Veà nhaứ hoùc baứi, xem laùi caực baứi taọp ủaừ chửừa. Veà nhaứ ủoùc baứi vaứ chuan bũ trửụực baứi: OÂn taọp chửụng I, theo noọi dung lớ thuyeỏt phaàn oõn taọp. * Rỳt kinh nghiệm :
Tài liệu đính kèm:
 giaoanhinh8chuong1cktkn.doc
giaoanhinh8chuong1cktkn.doc





