Giáo án Hình học Lớp 8 - Chương trình cả năm - Năm học 2007-2008 - Nguyễn Thị Anh Thơ
1. HĐ 1: (5) Kiểm tra bài cũ ? Tứ giác là gì? Tứ giác lồi là gì?
? Phát biểu định lý tổng 4 góc trong một tứ giác?
2. HĐ 2: (8) Định nghĩa hình thang ? Học sinh quan sát H13/73, cho biết tứ giác ABCD có gì đặc biệt? Vì sao? Dựa vào kiến thức nào?
? Hai cạnh AB và CD gọi là hai cạnh gì? Chúng có vị trí như thế nào?
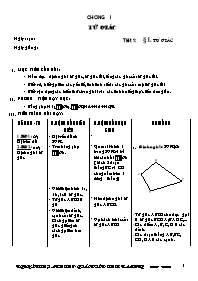
- Giáo viên giới thiệu tứ giác ABCD trên H13 là một hình thang.
? Hình thang là gì?
? Giáo viên vẽ một hình thang ABCD và giới thiệu cạnh đáy, cạnh bên, đáy lớn, đáy nhỏ, đường cao như trong SGK.
? Cho một hình thang thì em hiểu như thế nào?
? Một tứ giác có hai cạnh đối song song thì suy ra điều gì?
? Để chứng minh một tứ giác là hình thang hay không thì dựa vào đâu? 1. Định nghĩa: SGK/73
Tứ giác ABCD: AB//CD
ABCD là hình thang
AB, CD: cạnh đáy
AD, BC: cạnh bên
AH: đường cao
CÁC HĐ - TG HOẠT ĐỘNG CỦA GIÁO VIÊN VÀ HỌC SINH GHI BẢNG
3. HĐ 3: (5) Nhận dạng hình thang ? Làm .?1./73.
- Giáo viên treo bảng phụ .?1./73.
? Học sinh trả lời và giải thích tại sao. Chỉ rõ hai cạnh đáy của hình thang (các tứ giác ABCD là hình thang vì B=A1=600 – 2 góc so le trong)
? Hình 15a,b.
? (tứ giác EFGH là hình thang vì G+H=1800 – 2 góc trong cùng phía)
? Có nhận xét gì về 2 góc kề 1 cạnh bên của hình thang.
Chương I Tứ giác Ngày soạn: Ngày giảng: Tiết 1: Đ1. Tứ giác Mục tiêu của bài: Nắm được định nghĩa tứ giác, tứ giác lồi, tổng các góc của tứ giác lồi. Biết vẽ, biết gọi tên các yếu tố, tính tính số đo các góc của một tứ giác lồi Biết vận dụng các kiến thức trong bài vào các tình huống thực tiễn đơn giản. Phương tiện dạy học: Bảng phụ H1; .?1./68; .?3./69;H4+H5+H6/70. Tiến trình bài dạy: Các HĐ - TG H.động của giáo viên H.động của học sinh Ghi bảng 1.HĐ 1: (2’) Đặt vấn đề Đặt vấn đề như SGK. 2.HĐ 2: (10’) Định nghĩa tứ giác Treo bảng phụ .?1./68. Giới thiệu hình 1a, 1b, 1c là tứ giác. Tứ giác ABCD là gì? Giới thiệu đỉnh, cạnh của tứ giác. Cách gọi tên tứ giác giống như cách gọi tên tam giác Quan sát hình 1 trong SGK và trả lời câu hỏi .?1./68 (1d có 2 đoạn thẳng BC và CD cùng nằm trên 1 đường thẳng) Nêu định nghĩa tứ giác ABCD. Gọi cách khác của tứ giác ABCD Định nghĩa: SGK/68 A D C B Tứ giác ABCD còn được gọi là tứ giác BCDA; BADC,... Các điểm A, B, C, D là các đỉnh. Các đoạn thẳng AB, BC, CD, DA là các cạnh. Các HĐ - TG H.động của giáo viên H.động của học sinh Ghi bảng 3.HĐ 3: (5’) Giới thiệu tứ giác lồi Yêu cầu học sinh làm .?2./68 Giới thiệu hình 1a là tứ giác lồi. Tứ giác lồi là gì? Giới thiệu quy ước. Đưa ra định nghĩa tứ giác lồi dựa vào hình ảnh trực quan Tứ giác lồi: SGK/69 Chú ý: SGK/69 4.HĐ 4: (7’) Giới thiệu đỉnh, kề, góc Treo bảng phụ H2/69. Phát phiếu học tập Điền ra phiếu học tập. Một học sinh lên bảng. Trả lời .?3./69 5.HĐ 5: (10’) Tổng các góc trong tứ giác Phát biểu định lý tổng ba góc trong tam giác? Làm thế nào để tính được A + B + C + D? Phát biểu thành định lý. Làm .?4./69. Kẻ đường chéo AC của tứ giác Tính và cho biết kết quả. Làm .?5./69 Tổng các góc trong tứ giác: định lý: SGK/69. Tứ giác ABCD: A + B + C + D = 3600 6.HĐ 6: (11’) Củng cố và hướng dẫn về nhà Treo bảng phụ H4; H5/70. Làm bài 1/70. Học sinh tính. Làm bài 2a/70. Làm bài 4 H9/71 HDVN: Bài3; 5 BVN: 2b; 3; 4b; 5/71. Ngày soạn: Ngày giảng: Tiết 2: Đ2. Hình thang I. Mục tiêu của bài: Nắm được định nghĩa hình thang, hình thang vuông, các yếu tố của hình thang. Biết cách chứng minh một tứ giác là hình thang, là hình thang vuông. Biết vẽ hinh thang, hình thang vuông. Biết tính số đo các góc của hình thang, hình thang vuông. Biết sử dụng dụng cụ để kiểm tra một tứ giác là hình thang. Biết linh hoạt khi nhận biết hình thang ở những vị trí khác nhau (hai đáy nằm ngang, hai đáy không nằm ngang) và ở các dạng đặc biệt (hai cạnh bên song song; hai cạnh đáy bằng nhau). II. Phương tiện dạy học: Thước, ê-ke, bảng phụ .?1./73, bảng phụ H20/75. III.Tiến trình bài dạy: Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng HĐ 1: (5’) Kiểm tra bài cũ Tứ giác là gì? Tứ giác lồi là gì? Phát biểu định lý tổng 4 góc trong một tứ giác? HĐ 2: (8’) Định nghĩa hình thang Học sinh quan sát H13/73, cho biết tứ giác ABCD có gì đặc biệt? Vì sao? Dựa vào kiến thức nào? Hai cạnh AB và CD gọi là hai cạnh gì? Chúng có vị trí như thế nào? Giáo viên giới thiệu tứ giác ABCD trên H13 là một hình thang. Hình thang là gì? Giáo viên vẽ một hình thang ABCD và giới thiệu cạnh đáy, cạnh bên, đáy lớn, đáy nhỏ, đường cao như trong SGK. Cho một hình thang thì em hiểu như thế nào? Một tứ giác có hai cạnh đối song song thì suy ra điều gì? Để chứng minh một tứ giác là hình thang hay không thì dựa vào đâu? Định nghĩa: SGK/73 Tứ giác ABCD: AB//CD ị ABCD là hình thang AB, CD: cạnh đáy AD, BC: cạnh bên AH: đường cao D H cạnh đáy C A cạnh đáy B cạnh bên cạnh bên Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng HĐ 3: (5’) Nhận dạng hình thang Làm .?1./73. Giáo viên treo bảng phụ .?1./73. Học sinh trả lời và giải thích tại sao. Chỉ rõ hai cạnh đáy của hình thang (các tứ giác ABCD là hình thang vì B=A1=600 – 2 góc so le trong) Hình 15a,b. (tứ giác EFGH là hình thang vì G+H=1800 – 2 góc trong cùng phía) Có nhận xét gì về 2 góc kề 1 cạnh bên của hình thang. HĐ 4: (8’) Nhận xét Làm .?2.a/74. Học sinh vẽ hình, đầu bài cho biết gì? Yêu cầu gì? Cho hình thang ABCD có đáy là AB, CD thì suy ra điều gì? AD và BC là cạnh gì? Muốn chứng minh AD=BC thì làm như thế nào? (Xét rABC và rCDA). AB//CD ị ? (A1 = C1) AD//BC ị ? (A2 = C2) Còn điều gì nữa? (cạnh AC chung) Hai tam giác trên bằng nhau theo trường hợp nào? ị ? Có nhận xét gì về hình thang có 2 cạnh bên song song? Làm .?2.b/74. AB//CD ị ? rABC = rCDA theo trường hợp nào? (c.g.c) ị điều gì? Muốn chứng minh AD//BC thì phải có điều gì? Có nhận xét gì về hình thang mà có hai cạnh đáy bằng nhau? Nhận xét: SGK/74 HĐ 5: (7’) Khái niệm hình thang vuông Học sinh quan sát H17 trong SGK và cho biết cạnh bên AD của hình thang có vị trí gì đặc biệt? (vuông góc với hai đáy). Hình thang vuông: Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng Giáo viên giới thiệu định nghĩa hình thang vuông và vẽ hình. Để chứng minh 1 hình thang là hình thang vuông thì ta phải có điều gì? Nếu 1 hình thang có một góc vuông thì nó có là hình thang vuông không? Vì sao? ị dấu hiệu nhận biết hình thang vuông. Muốn chứng minh một tứ giác là hinh thang vuông ta phải chỉ ra mấy điều kiện? Dấu hiệu nhận biết hình thang vuông: SGK/74 HĐ 6: (8’) Dùng thước và ê-ke kiểm tra tứ giác là hình thang, tính góc của hình thang Làm bài 6/74. (ABCD; IKMN là hình thang; EFGH không phải là hình thang) Làm bài 7/75. Giáo viên treo bảng phụ. x=? Vì sao? (1000) y=? (1400) y=? (700 - so le trong) x=? (500 - đồng vị) x=? (900) y=? (1150) Có nhận xét gì về hình thang ABCD ở hình 20c/75? HĐ 7: (5’) Củng cố và hướng dẫn về nhà Làm bài 8/75. Vẽ phác hình và tính: AB//CD ị? (A + D = 1800) (A = 1000; D = 800) (B = 2C; B + C = 1800 ị B = 1200; C = 600) HDVN: Bài 9; 10/75 BVN: Bài 9; 10/75 Tiết 3: Đ3. Hình thang cân I. Mục tiêu của bài: Nắm được định nghĩa, các tính chất, các dấu hiệu nhận biết hình thang cân. Biết vẽ hình thang cân, biết sử dụng định nghĩa và tính chất của hình thang cân trong tính toán và chứng minh. Biết chưng minh một tứ giác là hình thang cân. Rèn luyện tính chính xác và cách lập luận chứng minh hình học. II. Phương tiện dạy học: Bảng phụ H23/76, giấy kẻ ô vuông. Tiến trình bài dạy: Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng 1.HĐ 1: (5’) Kiểm tra bàI cũ Hình thang là gì? Tính chất của hình thang? Thế nào là hình thang vuông? Dờu hiệu nhận biết hình thang vuông? 2.HĐ 2: (10’) Định nghĩa hình thang cân Học sinh quan sát hình 22 trong SGK và trả lời .?1./76. (C = D) Hai góc như thế nào? Giáo viên giới thiệu hình thang trên hình 22 là hình thang cân. Vậy thế nào là hình thang cân? Để một tứ giác là một hình thang cân thì có những điều kiện nào? Cho một hình thang cân thì suy ra điều gì? Làm .?2./76. Giáo viên treo bảng phụ H23/76. Tìm các hình thang cân? (ABCD; IKMN; PQST) Tính các góc còn lại của mỗi hình thang cân đó? (C=1000; I=1100; N=700; S=900) Có nhận xét gì về 2 góc đối của hình thang cân? (bù nhau) Định nghĩa: SGK/76 ABCD là hình thang cân (đáy AB; CD) Û AB//CD C = D Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng O A B D C 2 1 2 1 A B D C 3.HĐ 3: (10’) Tính chất của hình thang cân Đo độ dài hai cạnh bên của hình thang cân ở H22/76. Vẽ hình, ghi GT, KL của định lý 1. Để chứng minh AD = BC thì làm như thế nào? Có ABCD là hình thang cân thì suy ra điều gì? Trường hợp không có giao điểm thì sao? (AD//BC ị điều gì?) Dựa vào đâu? Vẽ hình thang cân ABCD, đáy AB, CD. Vẽ hai đường chéo của hình thang cân. Dự đoán gì? Học sinh chứng minh. Tính chất: Định lý 1: SGK/76 GT ABCD là hình thang cân (đáy AB, CD) KL AD = BC CM: SGK/77 Định lý 2: SGK/77 CM: SGK/77 4.HĐ 4: (10’) Dấu hiệu nhận biết hình thang cân Làm .?3./77. Dùng com pa vẽ các điểm A, B nằm trên m sao cho CA = DB. (lấy D làm tâm quay 1 cung tròn cắt m tại B; giữ nguyên khẩu độ compa, lấy C làm tâm quay 1 cung tròn cắt m tại A) Đo các góc của hình thang. Dự đoán hình thang ABCD có gì đặc biệt? Phát biểu thành định lý. Giáo viên: Định lý này sẽ được chứng minh ở bài 18. Để chứng minh một hình thang là hình thang cân thì ta có bao nhiêu cách? ị dấu hiệu nhận biết hình thang cân. Dấu hiệu nhận biết: Định lý 3: SGK/78 Dấu hiệu nhận biết: SGK/78 5HĐ 5: (5’) Đọc thêm 6.HĐ 6: (5’) Củng cố và hướng dẫn về nhà Nhắc lại định nghĩa hình thang. Dấu hiệu hình thang cân. Làm bài 13/79. HDVN: Bài 14; 15/79 Tiết 4: luyện tập Mục tiêu của bài: Rèn kỹ năng chứng minh tứ giác là hình thang cân dựa vào dấu hiệu nhận biết hình thang cân. Bước đầu cho học sinh biết suy luận, lập luận chặt chẽ. Phương tiện dạy học: Thước thẳng, giấy kẻ ô vuông. Tiến trình bài dạy: Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng HĐ 1: (5’) Kiểm tra bài cũ Thế nào là hình thang cân? Các tính chất của hình thang cân? Dấu hiệu nhận biết hình thang cân? B C A D E 1 2 1 2 HĐ 2: (30’) Luyện tập Chữa bài 15/79. Học sinh vẽ hình, ghi GT, KL. Muốn chứng minh tứ giác BDEC là hình thang cân thì ta phải chứng minh gì? Dựa vào kiến thức nào? Muốn chứng minh tứ giác BCED là hình thang thì phải chứng minh gì? B = ? Dựa vào đâu mà tính được? Bài 15/79: GT rABC cân tại A AD=AE; A=500 KL a) BDEC là hình thang cân. b) Tính B, C, D? Chứng minh Xét rABC cân ở A (gt) ị B = C (tính chất r cân) Có A+B+C=1800 (định lý tổng các góc trong r) ị A + 2B = 1800 B = Xét rADE có AD=AE (gt) ị rADE cân ở A (định nghĩa tam giác cân) ị D1=E1 (tính chất rcân) Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng B C A E D 1 2 1 2 1 D1 = ? Tính như thế nào? B và D1 là hai góc như thế nào? ị điều gì? B = ? Đọc đề bài. Vẽ hình, ghi GT, KL. Bài toán này có gì khác so với bài 15/79? Chứng minh AD=AE như thế nào? Có A+D1+E1=1800 (định lý tổng các góc trong r) ị A + 2D1 = 1800 D1 = Từ và ị B = D1 Mà hai góc này ở vị trí đồng vị ị DE//BC ị tứ giác BCED là hình thang (định nghĩa hình thang) Có B=C (CMT) ị BCED là hình thang cân (dấu hiệu nhận biết hình thang cân) Ta có: C=B ị D1 = 650 D1+D2=1800 (2 góc kề bù) ị 650+D2=1800 D2=1800-650=1150 E2=1150 Bài 16/79: GT rABC: AB=AC BD, CE là phân giác KL BECD là hình thang cân có DE=BE Chứng minh Xét rABC và rACE có: AB=AC (gt); A chung ; (BD, CE là phân giác), mà B = C (vì rABC cân) ị B1 = C1 ị rABC = rACE (g.c.g) ị AD=AE (2 cạnh t/ứng) Các HĐ - TG Hoạt động của giáo viên và học sinh Ghi bảng (CMT) Để chứng minh DE=BE ta chứng minh gì? Đã có dữ kiện gì? A B 1 1 1 1 D C E Vẽ hình, ghi GT, KL Để chứng minh hình thang ABCD là hình thang cân thì cần chứng minh gì? D1=C1 ị điều gì? AC = ? BD = ? Hình thang ABCD là hình thang ... 216 + 1314,4 = 1688,5 cm2 Hoạt động nhóm để tính trung đoạn SK? - Cho biết kết quả nhóm - Chữa + Tính diện tích xung quanh ? + Tính diện tích toàn phần? + Chốt lại phương pháp tính của toàn bài HS hoạt động theo nhóm HS : SK = =36,51 HS : Sxq = p.d = 12,3. 36,51 = 1314,4 cm2 Tính diện tích toàn phần Stp = Sxq + Sđ Stp = 216 = 1688,5 HS chữa bài GV: Nghiên cứu BT 50b/125 (bảng phụ) +Tính diện tích xung quanh của hình chóp cụt đều? + Gọi HS nhận xét và chữa HS : Vì các mặt bên của hình chóp cụt là các hình thang cân nên S1 = Sxq = S1.4 = 42 cm2 3. BT 50/125 b) S’AB’C’C = => Sxq = 4.S’ = 42 cm2 Hoạt động 3: Giao việc về nhà (2 phút) Tiết sau ôn tập chương IV: Làm các câu hỏi ô tập ở sgk Ôn lại các kiến thức cơ bản chương IV BTVN: 52,55,57/128,129 sgk Ngày soạn:6/4/08 Ngày giảng: Tiết 67: ôN TậP CHƯƠNG IV I- Mục tiêu - Hệ thống các kiến thức cơ bản chương IV -Vận dụng các công thức để tính diện tích và thể tích các hình đã học -Thấy được mối liên hệ giữa các kiến thức đã học với thực tế. II- Chuẩn bị - GV: Thước kẻ, bảng phụ - HS: Thước kẻ, Ôn lại kiến thức chương IV III- Tiến trình dạy học Hoạt động của GV Hoạt động của HS Ghi bảng Hoạt động 1:Kiểm tra bài cũ (5 phút) GV: Kiểm tra việc làm đề cương ôn tập của HS Hoạt động 2: Ôn tập (38 ph) GV: Nhắc lại đặc điểm của hình hộp chữ nhật + Thế nào là 2 đường thẳng song song trong không gian, cho ví dụ? + Nhắc lại khái niệm đường thẳng song song với mặt phẳng? Cho ví dụ? +Thế nào là a) Hai mặt phẳng song song b) Đường thẳng vuông góc với mặt phẳng c) Hai mặt phẳng vuông góc ? HS : 2 đáy là hình chữ nhật , các cạnh bên song song và bằng nhau HS là hai đường thẳng không có điểm chung và ... Ví dụ: 2 mép bảng HS : Khi chúng không có điểm chung. Ví dụ: đường thẳng mép bàn //mặt phẳng nền nhà HS phát biểu các kháiniệm trên và cho ví dụ liên hệ thực tế để minh hoạ. I- Lý thuyết A. Hình lăng trụ đứng 1. Hình hộp chữ nhật Hai đường thẳng song song : chúng không có điểm chung và thuộc một mặt phẳng + Đường thẳng song song mặt phẳng không có điểm chung + hai mặt phẳng song song không có điểm chung + Đường thẳng vuông góc với mặt phẳng + Hai mặt phẳng vuông góc ... V=a.b.c GV: Nêu cách tính diện tích xung quanh và thể tích của a) Hình lăng trụ b) Hình chóp đều Gọi HS páht biểu thành lời sau đó ghi theo kí hiệu để HS dễ thuộc. HS : 1 Hình lăng trụ - Thể tích bằng tích của diện tích đáy với đường cao của hình lăng trụ Diện tích xung quanh bằng tích 2 lần chu vi đáy và đường cao 2) Hình chóp - Thể tích bằng 1/4 tích diện tích đáy và đường cao. - Diện tích xq bằng tích nửa chu vi đáy và đường cao mặt bên 2) Hình lăng trụ V = S.h Sxq = 2p.h 3) Hình chóp đều Hình chóp + Đặcđiểm + Thể tích hìh chóp đều V = 1/3 S.h Diện tích xung quang Sxq = p.d GV: Nghiên cứu BT 51 ở bảng phụ Hãy thính diện tích xung quanh, diện tích toàn phần và thể tích ở các hình trên. + Chia lớp làm 4 nhóm Mỗi nhóm là 1 phần/ - Cho biết kết quả từng nhóm -Các nhóm chấm chéo lẫn nhau? - Đưa ra đáp án và cho điểm + Chốt lại phương pháp tính S,V HS : Nghiên cứu đề bài ở trên bảng phụ HS hoạt động theo từng nhóm HS đưa ra kết quả nhóm HS chấm chéo nhóm HS theo dõi bài của nhóm mình II. Bài tập 1) BT 51/127 a) Sxq = 4a.h Stp = 4ah +2a2 = 2a(2h+a) V= a2.h b) Sxq = 3ah Stp = 3ah + 2 V = c) Sxq = 6.a.b Sđ = 3/2a2. Stp = 6a.h + 3a2. V= d) Sxq = 5a.h Stp = 5ah + 2 = a(5h + ) Hoạt động 3: Giao việc về nhà (2 phút) - Học lại kiến thức trong chương 4 - Tiết sau kiểm tra 1 tiết - BTVN: 52,53/127 sgk Ngày soạn:13/4/08 Ngày giảng: Tiết 68 - 69: ôn tập cuối năm I- Mục tiêu - Hệ thống kiến thức cơ bản chương III và chương IV - Luyện tập dạng bài về tứ giác, tam giác đồng dạng, hình vuông, hình không gian - Rèn kĩ năng giải bài tập II- Chuẩn bị - GV: Thước kẻ, bảng phụ - HS: Thước kẻ, Ôn lại kiến thức ĩu III- Tiến trình dạy học Hoạt động của GV Hoạt động của HS Ghi bảng Hoạt động 1:Kiểm tra bài cũ (5 phút) GV: Phát biểu định lý Talet + Nhắc lại t/c đường phân giác trong tam giác? HS ; Nếu 1 đường thẳng cắt 2 cạnh của 1 tam giác và song song với cạnh còn lại thì nó tạo ra những cặp đoạn thẳng tỉ lệ HS đường phân giác trong tam giác chia cạnh đối diện thành 2 đoạn thẳng tỉ lệ với cạnh kề của nó I- Lý thuyết 1) Địnhlý Talet - Thuận - Đảo - hệ quả 2) T/c phân giác A1 = A2 => Yêu cầu HS ghi t/c theo hình GV; Nêu các trường hợp đồng dạng của 2 tam giác? HS nêu các trường hợp đồng dạng của 2 tam giác thường và các trường hợp đồng dạng của 2 tam giác vuông 3. Tam giác đồng dạng a) Tam giác: - c.c.c -g.g -c.g.c (Cạnh: tỉ lệ; góc:bằng nhau) b) tam giác vuông - Như tam gác - 1 góc bằng nhau + Yêu cầu HS xem lại lý thuyết chương IV ở tiết 69 HS: Ôn ại lý thuyết chương IV thêo vở đã ghi 4) Hình học không gian (sgk) Hoạt động 2:Bài tập (30 phút) GV: Nghiên cứu trên bảng phụ Cho DABC, các đường cao BD,CE cắt nhau tại H, đường vuông góc với AC tại C cắt nhau tại K. Gọi M là trung điểm BC.CMR a) ADB AEC b) HE.HC = HD.HB c) H,M,K thẳng hàng? + Trìnhbày lời giải phần a. + các nhóm thảo luận và tỉnh fbày lời giải phần b,c? + Gọi HS nhận xét và chốt phương pháp HS đọc đề bài ở trên bảng phụ - Lên bảng vẽ hình ghi GT - KL HS : trình bày ở phần gh bảng HS hoạt động nhóm Đưa ra kết quả nhóm HS nhận xét II- bài tập Bài 1: a) Xét DADB; DAEC D = E = 1V (gt) A: chung => DADB = DAEC (G.G) b) Xét DHEB ; DHDC Có E = D=1V (gt) EHB = DHC (đ) => DHEB = DHDC (g.g) => HE.HC = HD.HB b) BH//KC CH //KB => BHCL là hình bình hành (1) Mà MB = MC (gt) (2) Từ (1) và (2) => H,M,K thẳng hàng GV: Nghiên cứu bài 11/133 ở sgk? + Vẽ hình của bài 2? + Nhắc lại công thức tính thể tích hình chóp? - Diệntích đáy ntn? - Đường cao hình chóp tính ntn? - Tính thể tích hình chóp? + Nhắc lại công thức tính Sxq, Stp? HS ; Nghiên cứu đề bài HS : Vẽ hình ở phần ghi bảng HS: V=Sđ.h Sđ: diện tích đáy H: đường cao HS: Sđ == AD2 = 202 = 400 cm2 HS: SO2 = SA2 - AO2 Mà AO2 = AC: 2 = HS: V = 2586,7 cm3 HS : Sxq = p.d Stp = Sxq + Sđ Bài 2: a) Xét DABC, B = 1V có AC2 = AB2 +BC2 = 202 +202 = 800 => AC = 20 => AO = AC: 2 = 10 Xét SAO, o = 1V SO2 = SA2 - AD2 = 376 SO = 19,4 V = 1/3 Sđ.h = 1/3.202.19,4 = 2586,7 Yêu cầu HS hoạtđộng nhóm phần b, sau đó chữa HS hoạt động nhóm phần b và đưa ra kết quả b) Gọi H là trung điểm CD => SH ^CD Mà SH2 = SD2 - DH2 = 476 => SH = 21,8 Sxq = 1/2.80.21,8 = 782 cm2 Stp = 1272 cm2 Hoạt động 3: Giao việc về nhà (3 phút) - Ôn lại lý thuyết chương 3,4 -BTVN: 1,2,4/132,133 sgk Ngày soạn: Ngày giảng: Tiết 72: Kiểm tra học kỳ II I- Mục tiêu - Kiểm tra kiến thức đại số - hình học trong học kỳ II - Đáng giá chất lượng dạy - học của GV và HS - Rèn kĩ năng làm bài tập II- Chuẩn bị - GV: Đề kiểm tra - HS: Ôn tập kỳ II III- Tiến trình dạy học Bài 1: (2 điểm) Điền Đ-S a) Ta có thể nhân 2 vế của 1 pt với cùng một số thì được phương trìnhmới tương đương với phương trình đã cho. b) Ta có thể nhân cả hai vế của bất phương trình với cùng một số âm và đổi chiều bất phương trình thì được bất phương trình mới tương đường bất phương trình đã cho. c) Nếu hai cạnh của tma giác nnày tỉ lệ với hai cạnh của tam giác kia và một cặp góc của chúng bằng nhau thì hai tam giác đồng dnạg d) Nếu hai tam gáic đồng dạng với nhau thì tỉ số haiđường cao tương ứng bằng tỉ số trung tuyến tương ứng Bài 2: (2 điểm) Giải pt 1) 2) 3) (x - 3) (x+3) < (x+2)2 +3 Bài 3: (2 điểm) Lúc 7giờ một người đi xe máy khởi hành từ A với vận tốc 30 km/h, sau đó 1 giờ người thứ hai cũng đi xe máy từ A đuổi theo với vận tốc 45km/h. Hỏi đến mấy giờ, người thứ hai đuổi kipk người thứ nhất? Nơi gặp nhau cách A bao nhiêu km? Bài 4: (3 điểm) Cho ABC, A = 1V, AB = 6cm, AC = 8cm, kẻ đường cao AH a) Tính BC b) CMR: AB2 = BH.BC. Tính BH, HC c) Vẽ phân giác AD của A (D ẻBC). CMR: H nằm giữa BD Bài 5 (1 điểm) Cho hình hộp chữ nhật ABCDA’B’C’D’ có Ab = 10cm, BC = 20 cm, AA’ = 15 cm a) Tính thể tích hình hộp chữ nhật b) Tính độ dài đường chéo AC’ của hình hộp chữ nhật B- Đáp án Bài 1: (2 điểm) 1. S 0,5 điểm 2. Đ 0,5 điểm 3. S 0,5 điểm 4. Đ 0,5 điểm Bài 2: (2 điểm) 1. x = 1 0,75 điểm 2. Đ/k: x ạ±2 0,25 điểm Phươngtrình nghiệm đúng với mọi x ẻR 0,5 điểm 3. x >-4 0,5 điểm Bài 3: (2 điểm) Gọi thời gian người thứ hai đến gặp người thứ nhất là x (h) , x >0 thời gian người thứ nhất đến gặp người thứ hai là x +1 (h) 1 điểm Quãng đường người thứ nhất đi là: 30 (x +1) (km) Quãng đường người thứ hai đi là: 45x (km) Phương trình 45 x = 30(x +1) => x= 2 ẻ ĐK Vậy người thứ hai đuổi kipk người thứ nhất lúc: 7 +1+ 2 = 10 (h) Nơi gặp nhau cách A là : 45.2 = 90 km 1 điểm Bài 4 ( 3 điểm) 0,25 điểm a) BC2 =AB2 +AC2 = 62 +82 = 100 => BC = 10cm 0,75 điểm b) xét DABC và DHBA có A = H = 1V B: chung => D ABC = DHBA (g.g) => =>AB2 = BH.BC 0,75 điểm => BH = 3,6cm 0,25 điểm HC = 6,4 cm 0,25 điểm C0 AD là phân giác A => => => BD = 4,3 cm 0,5 điểm Trên BC có BH = 3,6 cm BD = 4,3 cm H nằm giữa B và D 0,25 điểm Bài 5: Hình vẽ 0,25 điểm a) V = a.b.c = 3000 0,25 điểm b) AC’ = Ngày soạn: Ngày giảng: Tiết 70: Kiểm tra CHƯƠNG iv I- Mục tiêu -Kiểm tra kiến thức chương IV - Đánh giá chất lượng dạy và học của GV - HS - Rèn kĩnăng giải bt vẽ hình không gian. II- Chuẩn bị - GV: Thước kẻ, đẻ kiểm tra - HS: Thước kẻ, Ôn lại kiến thức chương IV III- Tiến trình dạy học A- Đề bài Bài 1(2 điểm) Cho hình hộp chữ nhật ABCDA’B’C’D’. Hỏi đường thẳng AB 1) Song song với đường thẳng nào? 2) Vuông góc với đường thẳng nào? 3) Song song với mặt phẳng nào? 4) Vuông góc với mặt phẳng nào? Bài 2 (2 điểm) Điền đúng (Đ) hoặc sai (S) a) Hình hộp chữ nhật là 1 lăng trụ đứng b) Hình hộp chữ nhật là một lăng trụ đều c) Hai đường thẳng không song song thì phải cắt nhau d) Hình chóp có đáy là một tam giác đều là hình chóp đều Bài 3 (4 điểm) Một hình hộp chữ nhật có 3 kích thước là 3cm, 4cm,6cm a) Tính Stp b) Tính V? Bài 4 (2 điểm) Một hình chóp tam giác đều có 4 mặt là những tam giác đều cạnh 6cm, diện tích toàn phần của hình chóp đó là : a) 18 cm2 b) 26 cm2 c) 12 cm2 d) 27 cm2 B- Đáp án Bài 1: 1. DC,D’C,A’B’ 0,5 điểm 2. AD,BC,AA’,BB’ 0,5 3) mặt phẳng (DCáC’D’); mp (A’B’C’D’) 0,5 4) mặt phẳng (BCáC’B’); mp (ADD’A’) 0,5 Bài 2: a) Đ 0,5 điểm b) S 0,5 điểm c) S 0,5 điểm d) S 0,5 điểm Bài 3: Vẽ hình : 1.0 điểm a) Stp = 108 cm2 1,5điểm b) V = 72 cm2 1,5điểm Bài 4: 2 điểm IV- Giao việc về nhà - Tiết sau ôn tập - Ôn lại lí thuyết chương 2,3 Ngày soạn: Ngày giảng:
Tài liệu đính kèm:
 Hình8.doc
Hình8.doc





